Pensamiento Filosófico y Humanidades I: El ejercicio de filosofar y la perspectiva humanista

4.0 Crisis: una pérdida de confianza en el valor de la verdad

Hay un creciente escepticismo sobre si creer en proposiciones verdaderas —aquellas que concuerdan con la realidad, y no simplemente halagan nuestras preferencias partidistas— sigue teniendo importancia en la política. Los signos de esta crisis de la creencia son cada vez más evidentes.

Incluye, por un lado, la disposición de los políticos a repetir falsedades evidentes sin temor a corrección; y por otro, una disposición equivalente del público no solo a tolerarlas, sino a creerlas —o al menos a respaldarlas— a pesar de su falsedad manifiesta. Muchos repiten estas mentiras en línea y fuera de línea, marchando en solidaridad verbal con sus compañeros de partido, en abierta contradicción con los hechos.

Sin embargo, al igual que con el asalto a la democracia —cuyos enemigos continúan ondeando triunfalmente su bandera—, aquellos que más vehementemente denigran el valor de la verdad son los mismos que buscan apropiarse de la palabra. La reempaquetan con estilo orwelliano y la venden de nuevo a las masas.

Esta crisis de nuestro tiempo no se limita a ningún país, universidad, empresa, político ni ciclo electoral. Se extiende a lo largo de todas las líneas partidistas. Es una crisis interrelacionada, porque las ideas de verdad y democracia están profundamente conectadas: sin verdad, todas las formas de autoritarismo encuentran terreno fértil.

Para muchos, la política y la verdad ya no se mezclan: son agua y aceite. Nadie ha dudado nunca —señaló una vez Hannah Arendt con su característico filo— “de que la verdad y la política están en bastante malos términos entre sí”. Incluso cabe pensar, como ella misma advirtió, que “la naturaleza de la esfera política está en guerra con la verdad en todas sus formas”. Dondequiera que la política entra en escena, la razón se repliega, o se convierte —como escribió David Hume— en esclava de las pasiones. No deliberamos: racionalizamos. Escuchamos solo lo que queremos oír. Nuestros prejuicios anteceden a nuestros argumentos, y muchas veces pensamos con el instinto antes que con el juicio. Nos decimos a nosotros mismos “yo sé, ellos no”, incluso cuando lo que creemos saber es abiertamente falso.

El cerebro político rara vez es el cerebro racional. Es un cerebro sometido, movido por la necesidad de pertenencia, identidad, reacción. Como resultado, la política ha estado desde siempre en una relación tensa, incluso antagónica, con la verdad. No porque la verdad no importe, sino porque la verdad —cuando es incómoda— exige una valentía que la política raramente recompensa.

Este conflicto es particularmente agudo en el contexto de la política democrática, ya que esta exige deliberación entre ciudadanos libres e iguales. Para algunos, el antagonismo entre verdad y política democrática tiene sus raíces en una forma de injusticia epistemológica incubada desde la educación: una que empobrece la capacidad de los ciudadanos para distinguir entre conocimiento, creencia y propaganda. Esta deformación convierte el concepto mismo de “verdad” en algo ambiguo, casi metafísico, demasiado abstracto —dicen— como para ser útil en los intercambios reales de la deliberación pública.

Además, en muchos casos, la verdad es percibida con connotaciones autoritarias: como si estuviera depositada en una élite —política, técnica o intelectual— que la administra desde una posición de privilegio. Así, afirmar que cierto juicio político es “verdadero” se interpreta, no como una apelación a la razón común, sino como un intento de imponer un punto de vista, de consagrar una forma particular de poder. La verdad, en este marco, deja de ser una orientación compartida para convertirse en un instrumento de dominación simbólica.

Para otros, la política democrática —en su mar de pluralidad de puntos de vista considerados “razonables”— tiende a marginar la verdad referencial, verificada y sustentada en evidencia sólida, tal como la conciben las comunidades epistémicas rigurosas. En nombre de la tolerancia o del respeto a la diversidad de opiniones, se diluye la distinción entre argumentos bien fundamentados y simples afirmaciones sin sustento. Esto ha llevado a algunos a cuestionar si el pluralismo democrático, tal como se practica hoy, no debería incluir también un deber de exclusión epistémica: es decir, la responsabilidad de rechazar afirmaciones manifiestamente falsas, no como un acto de censura, sino como parte de una deliberación crítica, exigente y responsable.

Defender la verdad en la esfera pública no implica imponer una ortodoxia única, sino resistir la pereza intelectual que consiste en tratar todas las opiniones como igualmente válidas, sin evaluación crítica. El pluralismo auténtico exige una conversación abierta, sí, pero también nutrida por un compromiso con el conocimiento, la evidencia y la honestidad intelectual.

Esta situación, aunque preocupante, es comprensible. El concepto de verdad —como todo concepto filosófico fundamental— posee una complejidad que ha sido discutida durante siglos. Y es cierto que, especialmente en el terreno político, saber qué es verdad no siempre es fácil. Las evidencias pueden ser ambiguas, los contextos complejos, y las interpretaciones múltiples. Sin embargo, la idea básica de la verdad —como aquello que concuerda con los hechos, que puede ser justificado racionalmente, que resiste la mera opinión— no es ni incomprensible ni, mucho menos, antidemocrática.

Al contrario: sin algún compromiso compartido con la posibilidad de conocer y defender lo verdadero, la deliberación democrática pierde sentido. Si todas las afirmaciones son tratadas como igualmente válidas, incluso aquellas que carecen por completo de sustento, la política se convierte en un concurso de voluntades, no de razones. En este sentido, el rechazo a la verdad como criterio compartido no es una expresión de pluralismo, sino una forma sutil de nihilismo político.

Crisol de pensadores: perseguir objetivos de creencias verdaderas sobre el mundo. Son los cimientos de la justicia epistémica que la democracia necesita para florecer. Y es por eso que las mayores amenazas al valor de la verdad para las democracias surgen cuando ignoramos la ciencia, denigramos las prácticas de discusión libre de ideas, o cuando los medios de comunicación censuran los espacios destinados a la razón.

En el sentido más básico, las afirmaciones verdaderas son aquellas proposiciones que buscamos cuando hacemos preguntas sinceramente; son proposiciones que concuerdan con la forma en que las cosas son, no como esperamos o creemos que son. Comprender esa idea es aceptar que puede haber proposiciones verdaderas en las que nunca creeremos, y que el hecho de creer no las convierte en verdaderas, sin importar cuán poderoso pueda ser el creyente.

Sin embargo, este es precisamente el concepto amenazado en este momento en muchas sociedades, donde los movimientos autoritarios están alentando a las personas no solo a repetir mentiras escandalosas, sino a valorar menos la creencia verdadera que la lealtad a una ideología, o incluso a una persona o partido político. Desde esta perspectiva autoritaria, si la gente cree sus mentiras, mejor; pero también están de acuerdo con el compromiso más siniestro: que la gente actúe como si las mentiras fueran ciertas.

Esta es una de las razones por las que la popularidad de la política autoritaria —incluso cuando sus practicantes no están en el poder— es una amenaza directa a la democracia. Las democracias requieren que sus ciudadanos le digan la verdad al poder. Decirle la verdad al poder significa decir lo que es verdad, incluso si es incómodo o peligroso. Pero también significa estar comprometido con lo que es verdad, incluidas las verdades que los autoritarios quieren borrar de la historia.

Cuando la verdad deja de valorarse en la política —de derecha o de izquierda—, cuando nos permitimos encogernos de hombros o ignorarla, ambas tareas cruciales se vuelven más difíciles, incluso imposibles. Dejamos de decirle la verdad al poder y, en cambio, le decimos al poder lo que quiere escuchar, solo para asegurarnos de que estamos sometidos a su fuerza autoritaria.

Valorar la verdad en la democracia no significa que todos deban creer las mismas cosas. Eso ni siquiera es posible, y mucho menos democrático. Valorar la verdad significa invertir en aquellas instituciones y prácticas colectivas que nos ayudan a buscar la verdad, adquirir conocimiento en lugar de mentiras, hechos en lugar de propaganda, derechos laborales en lugar de deseos volátiles. El problema de fomentar una organización social más racional es el problema real de la política. Esto se debe a que participar en democracia significa tratarnos unos a otros como personas capaces de basar nuestras opiniones en evidencia histórica. Pero no podemos hacerlo si la comunidad no protege y practica una relación con la información que sea coherente con lo real.

Es por eso que las universidades de todo el mundo deben redoblar urgentemente su compromiso con la epistemología en sus currículos, ya que esta sustenta la búsqueda de la verdad. Eso significa proteger la ciencia y la historia de la intrusión política que las corrompe. Significa una educación temprana dirigida no solo a la alfabetización en la disertación, el diseño experimental, el modelado matemático y la narrativa literaria de vanguardia, sino también a enseñar a los estudiantes los conceptos erróneos comunes y las técnicas apropiadas para detectar información sesgada en la era de la inteligencia artificial. En este país, significa tener el coraje de apostar por el progreso ético y por una autonomía intelectual de la comunidad académica que sea verdaderamente asequible.

Incluso los alados de la democracia a menudo no aprecian plenamente el valor central que representa la verdad para ella, habiéndose convencido de que la verdad es un concepto demasiado difuso para tomarse en serio en política.

Una tarea central de las universidades es corregir esas suposiciones: convencer no solo de que el concepto de verdad puede ser rehabilitado como justicia epistémica, sino de que la democracia lo exige.

En mi opinión, la tradición filosófica que representa Dewey —el pragmatismo estadounidense— nos ofrece la mejor esperanza para una rehabilitación filosófica de la verdad en la política.

Para el filósofo y lingüista Noam Chomsky, lo que ha debilitado a la democracia es “una mera transferencia de conocimiento, consumido a través de la memorización y luego regurgitado en exámenes estandarizados^[1]”. Lejos de tener una universidad comprometida e involucrada con el desarrollo del pensamiento independiente y crítico, las mentes de los estudiantes están anestesiadas, como el poeta John Ashbery capta con precisión en “¿Qué es la poesía?: En la escuela todos los pensamientos se peinaron, lo que quedaba era como un campo^[2]”.

Charles Sanders Peirce etiquetó como concordancia aquello que perseguimos durante la investigación académica. Para Peirce, las respuestas concordantes son aquellas que sobreviven a los fuegos de la experiencia, resisten el escrutinio racional a largo plazo y no entran en conflicto con los hechos empíricos. Esta es la idea que puede ayudarnos a comprender la verdad en la política. Las proposiciones políticas son verdaderas cuando forman parte de una visión concordante de las prácticas políticas y sociales humanas: una visión que se mantiene unida internamente, pero que también concuerda con los hechos que existen fuera del ámbito político.

Por desgracia, en nuestra política polarizada, tendemos a dar sentido a casi todo desde la ideología. Pero el mundo es más grande que la política humana. Los hechos —o las verdades— sobre este mundo más amplio son independientes de los seres humanos, de una manera que la verdad política nunca puede serlo.

Ese es el punto clave que incluso algunos pragmatistas a veces no aprecian completamente: para explicar la verdad en política, debemos evitar suponer que la verdad viene en un solo tipo. La verdad política —y la realidad política— puede hacer que te persigan, censuren, lastimen o incluso maten. Nada es más real que eso. Pero es un error pensar que nuestros juicios políticos son verdaderos exactamente de la misma manera que nuestros juicios sobre las rocas, los enlaces químicos o los árboles. Las verdades de este último tipo representan un mundo independiente del humano. Decir la verdad en política, en cambio, implica ofrecer explicaciones concordantes: explicaciones que sean coherentes tanto con el mundo humano como con el mundo que va más allá de lo humano.

4.1 Deflacionismo: discurso de explicación de la verdad

Las especies tradicionales de inflacionismo incluyen teorías de la verdad por correspondencia, verdad por coherencia, pragmáticas de la verdad, primitivas de la verdad, verdad por predicción. En filosofía analítica de la verdad se suele hablar de teorías inflacionarias (o robustas) frente a teorías deflacionarias (o minimalistas).

Las inflacionarias consideran que la verdad es una propiedad sustantiva que añade algo importante más allá de la mera aserción. Dentro de ellas se suelen distinguir varias especies clásicas:

Teoría de la correspondencia: la verdad consiste en la relación entre las proposiciones y los hechos (un enunciado es verdadero si corresponde con la realidad).

Teoría de la coherencia: la verdad depende de la coherencia de una proposición dentro de un sistema o red de creencias.

Teorías pragmatistas: la verdad se identifica con lo que resulta útil, satisfactorio o con lo que “funciona” en la práctica (Peirce, James, Dewey, etc.).

Teoría de la redundancia/primordialidad (primitivas de la verdad): sostienen que “verdadero” es una noción básica que no puede definirse en términos más fundamentales, pero sí se usa para explicar fenómenos lógicos o semánticos.

Teorías predictivistas o verificacionistas (como las del positivismo lógico): identifican la verdad con la verificabilidad empírica o con el éxito predictivo de los enunciados.

Las especies en el género del deflacionismo se entienden mejor no como teorías de la verdad, sino, más bien, como diversas teorías del discurso sobre la verdad; es decir, como distintas explicaciones acerca de la mejor manera de comprender y explicar el funcionamiento de una teoría particular (fragmento). El fragmento de discurso en cuestión (el discurso de la verdad) puede circunscribirse como aquel que emplea lo que podemos llamar locuciones aléticas (por ejemplo: es verdadero, es falso, es verdadero que, es necesario que, es posible que, es imposible que). Después de todo, muchos defensores del deflacionismo niegan que exista alguna propiedad robusta de la verdad; y aquellos deflacionistas que conceden que “es verdadero” atribuye una propiedad, toman esta propiedad como “delgada” o insustancial. Como señala Leon Horsten: “el deflacionismo es una etiqueta para una conexión suelta de puntos de vista más precisos que comparten un parecido familiar entre sí^[3]”.

¿La verdad es una propiedad con peso ontológico o solo una función en el discurso? Al destacar el papel de las locuciones aléticas, es un punto clave: no se trata tanto de lo que “es” la verdad, sino de cómo hablamos de ella y cómo esas expresiones cumplen funciones en la práctica discursiva.

El deflacionismo es un nuevo enfoque del tema de la verdad desarrollado en el siglo XX como una alternativa al inflacionismo. El enfoque inflacionario abarca todas las teorías tradicionales de la verdad. Lo que estas teorías tienen en común es una serie jerárquica de suposiciones sobre las locuciones aléticas más centrales, así como sobre los conceptos aléticos y las propiedades aléticas que supuestamente expresan y atribuyen. Todas las teorías tradicionales de la verdad presuponen o asumen:

1. Las locuciones aléticas (centralmente, “verdadero/a”) funcionan lógicamente como predicados.

2. Los predicados expresan conceptos o “atributos”, constructos y, por lo tanto, sirven para describir o caracterizar a los supuestos portadores de la verdad.

3. Estos conceptos atributivos determinan propiedades aléticas, cuya posesión (o falta de ella) se atribuye en las descripciones que proporcionan los usos de las locuciones aléticas.

4. Las propiedades aléticas atribuidas a través de las locuciones aléticas tienen una naturaleza robusta (o sustantiva).

Locuciones aléticas son aquellas expresiones o enunciados que atribuyen, niegan o se refieren al valor de verdad de una proposición. es una expresión lingüística cuyo contenido o función está relacionado con la verdad o falsedad de una proposición.

Ejemplo:

“Es verdadero que la Tierra gira alrededor del Sol.”

“Es falso que el fuego sea frío.”

“Debe ser verdad que llovió ayer.”

En estos casos, las palabras “es verdadero”, “es falso”, “debe ser verdad” son locuciones aléticas porque se refieren explícitamente a la condición de verdad de lo dicho.

Las modalidades aléticas o también llamado tipos principales de propiedades aléticas más comunes son:

Necesario que p → (□p)

Posible que p → (◇p)

Imposible que p → (¬◇p o ¬p es posible)

Contingente que p → (p y ¬p son posibles)

propiedad alética de la verdad que proporcionan las diferentes teorías. Todas ellas también presuponen que las locuciones aléticas desempeñan el papel semántico de atribuir la posesión (o la falta) de la propiedad de la verdad (o de la falsedad) a los portadores de la verdad, que generalmente se consideran como elementos tales como oraciones, símbolos oracionales, enunciados, cláusulas, proposiciones, afirmaciones, creencias o juicios. Una consecuencia de la suposición de que “es verdadero” es un predicado descriptivo consiste en que no hay “equivalencia de significado” entre una oración o proposición y una descripción de verdad de esa oración o proposición.

Como consecuencia, para los inflacionistas sobre la verdad, una atribución de verdad como “la nieve es blanca” no agota el análisis de la relación entre lenguaje y mundo. Un inflacionista, por supuesto, reconocerá algún tipo de equivalencia entre cada portador de la verdad y una atribución de verdad a él, una equivalencia expresada en los ejemplos de la versión preferida del teórico mediante el esquema de verdad neutral:

(TS) [p] es verdadera sí y solo si p.

Identificar (TS) como un esquema es reconocer que consiste en una especie de plantilla compuesta de palabras y símbolos, junto con ciertas reglas o condiciones que indican cuáles son los “rellenos” o “instancias” de dicha plantilla. Para (TS), esas condiciones especifican que p es una variable que se completa con oraciones (declarativas) en lenguaje natural, que los corchetes representan algún dispositivo de nominalización o denominación no especificado, y que “iff” (es decir, sí y solo si) indica una equivalencia no específica, una combinación de implicación e implicación inversa que no es necesariamente material.

Entendido de esta manera, un esquema es realmente una especie de sistema que tiene la capacidad de generar un número infinito de instancias del mismo. En el caso de (TS), genera las equivalencias de verdad, a veces llamadas sentencias T o bicondicionales T. Para los inflacionistas, estas equivalencias de verdad son atribuidas mediante el uso del predicado de verdad. La mayoría de los inflacionistas sostiene que tales equivalencias requieren una explicación sustantiva que involucre un análisis de esa propiedad en términos de conceptos más básicos y de ciertas propiedades y relaciones fundamentales que dichos conceptos determinan. En el fondo, es la tensión entre la descripción del predicado “verdadero” y su capacidad de fundamentación filosófica: el inflacionismo no se conforma con la mera equivalencia formal, sino que busca dotar a la verdad de un lugar ontológico o conceptual. Has logrado expresar eso sin perder rigor.

Por el contrario, un deflacionista tomará los ejemplos de su versión preferida del esquema (TS) como conceptualmente básicos y explicativamente fundamentales, o simplemente como productos triviales e inmediatos del modo en que opera el predicado de verdad desde una perspectiva lógico-lingüística. Como resultado, los deflacionistas sostienen que el “es” en los casos del esquema (TS) indica una equivalencia muy fuerte entre los lados izquierdo y derecho de estos bicondicionales. Por lo tanto, los deflacionistas reconocen y rechazan al menos algunos de los supuestos y presuposiciones estándar que generan las teorías inflacionarias de la verdad, resistiéndose a postular una propiedad de verdad sustantiva. En cambio, ofrecen una nueva comprensión tanto del concepto de verdad como del funcionamiento de las locuciones aléticas. Por esta razón, en lugar de una propiedad de la verdad, las diversas variantes del deflacionismo —como las teorías del discurso de la verdad o las teorías del concepto de verdad— reformulan el problema. En este contexto, las nociones de una “propiedad de verdad” o de “probadores de verdad” suelen ser reemplazadas por la noción de atribuir el predicado de verdad a ciertos enunciados u objetivos de aplicación. Es decir, deflacionismo: no negar la utilidad del término “verdad”, sino restringir su alcance ontológico. En lugar de buscar una entidad o propiedad metafísica que fundamente la verdad, el deflacionismo desplaza la cuestión hacia el uso lingüístico del predicado, mostrando que decir “es verdad que p” no añade contenido a la afirmación “p”.

Dos corrientes son predominantes en el pensamiento y la cultura moderna. Por un lado, hay un intenso compromiso con la veracidad —o, en todo caso, una suspicacia generalizada, una disposición a no ser engañados, un afán de ver a través de las apariencias las verdaderas estructuras y motivos que subyacen detrás de ellas. Sin embargo, junto con esta exigencia de veracidad —o, para decirlo de manera menos positiva, este reflejo contra el engaño—, hay una sospecha igualmente generalizada sobre la verdad misma: si existe tal cosa; si no la hay; si puede ser más que relativa o subjetiva, o algo por el estilo; y, en conjunto, si debemos preocuparnos por ella en el desarrollo de nuestras actividades o al dar cuenta de ellas. Estas dos cosas —la devoción a la veracidad y la sospecha dirigida a la idea de verdad— están conectadas entre sí. El deseo de veracidad impulsa un proceso de crítica que debilita la seguridad de que existe una verdad firme o incondicionalmente afirmable.

La sospecha se apodera porque los relatos que se han ofrecido como portadores de la verdad sobre el pasado a menudo resultan ser sesgados, ideológicos o interesados. Pero los intentos de reemplazar estas distorsiones con “la verdad” pueden tropezar, una vez más, con el mismo tipo de objeción. Entonces surge la cuestión de si cualquier relato puede aspirar a ser, simplemente, verdadero: si la verdad objetiva —o la verdad en absoluto— puede considerarse honestamente como el objetivo del estudio. Pero si la verdad no es el objeto de nuestro estudio en la universidad, entonces debe aceptarse que nuestra situación implica prescindir de la verdad para el progreso ético.

Podemos ver cómo la exigencia de veracidad y el rechazo de la verdad pueden ir de la mano. Sin embargo, esto no significa que puedan coexistir felizmente, ni que la situación sea estable. Si realmente no crees en la existencia de la verdad, ¿por qué la pasión por la veracidad? O, como también podríamos decir: en la búsqueda de la veracidad, ¿a qué se supone que estás siendo fiel? No se trata de una dificultad abstracta ni de una paradoja. Tiene consecuencias para la política real, y señala el peligro de que nuestras actividades intelectuales —particularmente en las humanidades— puedan hacerse pedazos. La tensión entre la búsqueda de la veracidad y la duda de que haya realmente alguna verdad que se pueda encontrar se manifiesta en una dificultad significativa: el ataque a alguna forma específica de verdad —como, en el caso que he mencionado, la verdad llamada historia— depende en sí mismo de algunas afirmaciones u otras que, a su vez, tienen que ser tomadas como verdaderas. De hecho, en el caso de la historia, esas otras reclamaciones serán reclamaciones del mismo tipo.  Incluso la crítica más radical se apoya, en última instancia, en alguna confianza —por mínima que sea— en la posibilidad de decir algo verdadero. La honestidad intelectual no exige certezas absolutas, pero sí el coraje de sostener algunas verdades como provisionales, frágiles, pero necesarias para que el pensamiento no se disuelva en pura sospecha.

Aquellos que dicen que todos los relatos históricos son construcciones ideológicas se basan, sin embargo, en una historia que debe reclamar la verdad histórica. Muestran que historiadores supuestamente “objetivos” han contado tendenciosamente sus relatos desde alguna perspectiva particular política; describen, por ejemplo, los sesgos que se han entretejido en la construcción de diversas historias de México. Tal relato, como una pieza particular de la historia, puede muy bien ser cierto. Pero la verdad es una virtud vergonzosamente inútil para un crítico que no solo quiere desenmascarar a los historiadores del pasado de México, sino también afirmar que, al final del camino, no hay verdad histórica. Es notable lo complacientes que pueden ser algunas historias “deconstructivas” respecto al estatus de la historia que despliegan.

4.2 El pálido tinte del pensamiento 

El matiz nativo de la razón, en el principio, fue un motivo. El motivo debió haber sido urgente: no parece que muchas deliberaciones hayan precedido a la acción que provocó. Cualquier acción precipitada es arriesgada, pero para una empresa particularmente trascendental —como la creación de un universo— el riesgo se ve agravado por la dificultad de saber de antemano cómo resultarán las cosas.

En un proyecto de esta magnitud, al menos tendría sentido tomárselo con calma, dejar que el polvo se asiente y mirar a su alrededor antes de pasar a la siguiente etapa: Y dijo Dios: hágase la luz. Y fue la luz. Y vio Dios la luz, que era buena.

Sin embargo, la autosupervisión rara vez es un enfoque eficaz para el control de calidad. Como podrían argumentar los gnósticos, el acto bíblico de la creación podría haberse beneficiado de una revisión previa al lanzamiento a gran escala, dado que su producto es tan radicalmente defectuoso (atestigua el sufrimiento generalizado e inevitable en el mundo).

Suponiendo que las intenciones por parte del responsable hayan sido buenas, este resultado —aunque imperfecto— debería hacer reflexionar a cualquier aspirante a creador de mundos: entre la idea y la realidad, entre el movimiento y el acto, cae la sombra.

Es posible que los meros seres finitos como nosotros no estemos en el negocio de crear universos enteros (todavía), pero rutinariamente tratamos de rehacer lo que podemos de nuestro pequeño mundo para nuestro beneficio, a través de nuestras acciones. En ese intento, nos encontramos con fracasos ocasionales, y las consecuencias de estos pueden no ser menos trascendentales para nosotros —y para los demás— de lo que un universo defectuoso habría sido para su creador (si este no se hubiera escudado de la responsabilidad hacia sus habitantes permaneciendo fuera de él). Una mala racha de intentos abortados puede conmocionar a una persona y llevarla a la pasividad por el resto de su vida. En resumen, traslada el problema de la creación fallida —antes atribuido a una divinidad— al terreno humano, personal y cotidiano. La analogía es sutil pero eficaz: así como un universo defectuoso puede ser catastrófico para sus criaturas, también lo puede ser un fracaso existencial para quien intenta modificar su mundo sin éxito. La crítica al creador que “permanece fuera de su mundo” se puede leer como una acusación al abandono, a la irresponsabilidad ante el dolor humano, pero también como un espejo de nuestras propias evasiones.

La inacción no es inherentemente más segura que la acción, ni moralmente preferible a ella. No lo es en la guerra —precisamente porque uno nunca puede estar seguro de que todos los demás se abstendrán de una acción hostil—. Y para quienes están presenciando el ejercicio de un poder que causa sufrimiento a otros, no hacer nada es también tomar una postura moral. Aun así, parece aconsejable aprender a desconfiar de los propios motivos, deseos y creencias, y, para aquellos que se consideran dignos, tratar de anticipar las consecuencias de la acción y de la inacción antes de comprometerse con una decisión. Y ahí, como dice Hamlet, está el problema. La famosa duda de Hamlet es profundamente humana y, sin embargo, está arraigada en rasgos mentales que compartimos con muchas otras especies. Si observamos a un gato envejecido considerar un salto dudoso entre dos muros, sospecharemos que lo que dijo William James es cierto: donde la indecisión es grande —como antes de un salto peligroso—, la conciencia es angustiante e intensa.

Las razones detrás de la agonía de la vacilación y la indecisión tienen tanto que ver con la naturaleza del mundo que habitamos como con la naturaleza humana —o felina—. La razón principal es la complejidad desmesurada de la red de causa y efecto: las posibles repercusiones de cualquier acto —o de una inacción impotente— se ramifican exponencialmente, especialmente en los asuntos humanos, a medida que uno trata de anticipar el futuro. Incluso si se conocieran todos los parámetros relevantes de la situación, e incluso si nuestro razonamiento a partir de esas premisas fuera impecable, ninguna cantidad de reflexión puede igualar tal complejidad. Es necesario cortar esquinas, hacer aproximaciones; e incluso entonces, en algún momento se debe lanzar la suerte antes de que todas las percepciones deseadas estén listas.

La complejidad del pensamiento prospectivo se ve agravada por la dificultad de la previsión emocional. En cada etapa de la avalancha creciente de posibles acontecimientos desencadenados por el acto en cuestión, es probable que experimentemos emociones diversas. Lo que podrían ser esas emociones depende, de forma compleja, tanto de la historia personal como de la situación futura que solo podemos imaginar imperfectamente. A medida que el implacable “tiempo” nos arrastra hacia ese futuro, la acción nos prepara para un posible “arrepentimiento”.

4.3 La persona de acción considera que lo que sabes que no sabes puede lastimarte

Desde el principio hasta el fin, la acción está acosada —y a veces empañada— por problemas: desde deseos irresponsables, pasando por información incompleta y razonamientos imperfectos, hasta consecuencias irreparables y arrepentimientos. Sin embargo, detenerse hasta el cansancio en las trampas potenciales no hará que desaparezcan ni que uno sea más feliz. Así que, como dijo Hamlet, la conciencia nos hace cobardes a todos, y así el matiz nativo de la resolución se enferma con el pálido tono del pensamiento, y las empresas de gran médula y momento desvían sus corrientes y pierden el nombre de acción.

Después de tanta deliberación, más vale actuar. Al diablo con las consecuencias. Al final, esa fue la elección de Hamlet, y no se arrepintió. La mayoría de nuestras empresas cotidianas no son tan trascendentales como la suya, y la mayoría de ellas no significan la muerte. La vida es aquello a lo que nos aferramos, y es lo inesperado lo que hace que la vida sea posible.

Es justo decir que la ambición es para el cuerpo político lo que la sal de mesa es para el cuerpo humano: imposible vivir sin ella, pero acorta seriamente la vida si se usa en exceso. Esto sugiere que la ambición debería estar sujeta al principio de los datos: ninguna sociedad moderna tiene la ambición de todos en el punto óptimo entre demasiado y demasiado poco.

Mi conjetura es que la dinámica social de la ambición es la culpable. Muchas personas tienen lo que contaríamos como la cantidad justa de ambición, pero algunas son ambiciosas más allá de los límites de la prudencia y la justicia —para usar la frase de Adam Smith—. El mero hecho de observar a esos luchadores y escaladores en acción es probablemente suficiente para sacar a los miembros de la modesta mayoría de su punto de equilibrio. Algunos contraen indefensión aprendida (como cuando se encuentran bajo el poder de un advenedizo) y terminan deprimidos. Muchos otros ven avivada su propia ambición y se ven arrastrados a la carrera de ratas, solo para experimentar una continua decepción con sus logros, ya que estos no logran mantenerse al día con sus aspiraciones.

Siendo la ambición un fenómeno fundamentalmente interpersonal, la comparación social que implica es una fuerza con la que todas las sociedades deben lidiar. Con muy pocas excepciones, nuestras economías y nuestra política están impulsadas por la ambición de “piel y lugar”. Adam Smith, una figura decorativa del Siglo de las Luces a quien a menudo se hace referencia como el padre fundador del capitalismo, señaló que la piel y el lugar —economía y política— son inseparables.

“Los objetos de la avaricia y de la ambición difieren solo en su grandeza. Un avaro está tan furioso por media moneda como un hombre ambicioso por la conquista de un reino.”

La famosa idea detrás del otro libro de Smith, La riqueza de las naciones, es que la ambición económica de cada persona tendría, como efecto secundario, el beneficio de la sociedad en su conjunto. Esta noción ha sido presentada como una explicación del enorme crecimiento económico que el mundo ha experimentado en los dos últimos siglos. Sin embargo, existe una explicación alternativa: que dicho crecimiento ha sido impulsado por la explotación de la mayoría a manos de unos pocos excesivamente ambiciosos.

Sea como fuere, el crecimiento es un fenómeno problemático. Por un lado, hace posible la mejora económica personal, y es difícil culpar a la gente por querer estar tan bien como sus vecinos. Por otro lado, una incesante carrera armamentista global por los niveles de vida, que estimulada por la búsqueda de ganancias por parte de aquellos que se benefician del consumo de otros, existe un crecimiento constante. Esto, cuando se compone, se vuelve exponencial, lo que, como nos dicen las matemáticas, es insostenible cuando los recursos de los que depende son finitos.

Con un solo planeta por explotar, la inminente escasez de recursos obliga cada vez más a que el luego económico se adelante suma cero: la ganancia de una persona debe ser la pérdida de otra persona, o de muchas otras personas. Así, la naturaleza del crecimiento hace que la ambición, ya sea meramente de autopromosión o de dominación de los demás, sea problemática también, en un sentido puramente empírico-económico. También es un problema de ansiedad y estrés innecesarios. Y ni siquiera está garantizado que conduzca al éxito profesional. ¿Por qué no podemos todos relajarnos un poco? 

Una razón por la cual un estado de moderación general en asuntos de ambición —que es lo que Adam Smith defendía— resulta inestable en el tiempo puede encontrarse en la dinámica misma del poder. Como observó Hannah Arendt, el poder, al igual que la acción, no tiene límites físicos: no está restringido por la naturaleza corporal del ser humano, como ocurre con la fuerza. Su única limitación real es la existencia de otras personas. Pero esta no es una limitación accidental, sino estructural, ya que el poder humano nace precisamente de la condición de pluralidad. Por lo tanto, la naturaleza del poder parecería garantizar que, mientras exista una sociedad, la ambición estará siempre en riesgo de desbordarse.

Adam Smith ilustró con sabiduría: nunca entres en esa obra de la que tan pocos han podido regresar; no te adentres en el círculo de la ambición; no te compares con esos amos de la tierra que ya han absorbido la atención de la mitad de la humanidad antes que tú.

Muchas creencias supersticiosas surgen porque se interpreta como causalidad lo que en realidad es solo coincidencia. Sin controles adecuados, no se obtiene evidencia confiable. Determinar relaciones de causa y efecto es una de las principales formas de dar sentido al mundo, y en el ámbito científico, los experimentos controlados aleatorios son el estándar de oro para lograrlo.

Para probar si una causa C genera un efecto E, no basta con observar los casos en los que  C ocurre; es necesario compararlos con aquellos en los que C no se presenta. Este grupo sin la causa se denomina grupo de control. Si el efecto E ocurre tanto con como sin C, entonces no se puede concluir que C sea la causa de E. Un ejemplo común es el de los ensayos clínicos. Si el grupo que recibe un nuevo compuesto no muestra mejores resultados que el grupo de control que recibe un placebo (una pastilla sin principio activo, como una pastilla de azúcar), entonces no hay evidencia suficiente para afirmar que el compuesto funciona. Aunque esta lógica parece simple, los experimentos pueden volverse rápidamente complejos, ya que es fundamental asegurarse de que no existan otros factores que puedan distorsionar o confundir los resultados.

Tal vez al grupo que recibió el compuesto le fue mejor, pero no gracias a la causa C, sino debido a algún otro factor correlacionado con C que en realidad produjo el efecto. Sin embargo, es común que controlar todos los factores posibles resulte difícil o incluso inviable. Por esta razón, la asignación aleatoria de los participantes al grupo experimental o al grupo de control es una herramienta fundamental: se presume que esta distribución aleatoria equilibra, en promedio, los demás factores relevantes entre ambos grupos.

Pero, ¿qué sucede si la mejora observada no se debe al efecto real de C, sino a la creencia del sujeto en la eficacia de C? Este es el llamado efecto placebo. Para evitarlo, es crucial que los participantes estén ciegos respecto al grupo al que pertenecen: ni deben saber si están recibiendo el tratamiento o el placebo. Sin embargo, incluso esto puede no ser suficiente.

Los investigadores mismos pueden influir inadvertidamente en los resultados si saben qué participantes reciben el tratamiento. Por ello, se utilizan ensayos doble ciego, en los que ni los participantes ni los experimentadores saben quién pertenece a qué grupo, al menos hasta después de que se hayan recogido todos los datos. Aun así, es posible que se observen diferencias entre los grupos por simple azar. Para determinar si los resultados tienen peso real, se debe realizar un análisis estadístico riguroso que permita establecer si las diferencias encontradas son estadísticamente significativas, es decir, si es poco probable que hayan ocurrido por mera casualidad.

Y aún hay más consideraciones: ¿los instrumentos están correctamente calibrados? ¿Se garantiza la integridad, pureza y conservación de las sustancias? ¿Las muestras están libres de contaminación? ¿Se ha verificado que no existan errores en el algoritmo computacional o en los modelos matemáticos utilizados? ¿La interpretación de los datos es consistente con el marco teórico? Como recordaría Richard Feynman, se necesita no solo aplicar la metodología científica, sino también el más alto estándar de honestidad intelectual. Un estudiante de ciencias pronto descubrirá que la ciencia exige mucho más que aplicar procedimientos: exige escrutinio, humildad, vigilancia constante y apertura al error, si de verdad se busca realizar y confirmar un descubrimiento auténticamente científico.

Una vez más, es importante tener en cuenta lo que está en juego cuando se habla de la asistencia que brindan los métodos apropiados en la práctica científica. Como bien señalaba Richard Feynman, hacer ciencia no es solo aplicar procedimientos, sino prestar una atención rigurosa a las condiciones que permiten emitir un juicio válido sobre el valor del trabajo realizado. Esto implica preguntarse, entre otras cosas: ¿qué tan sólida es la evidencia que respalda una conclusión? ¿Qué grado de confianza es razonable tener en un supuesto descubrimiento?

Estas preguntas no son meramente técnicas: son cuestiones normativas, pues implican valorar la calidad del razonamiento, la fiabilidad de los datos, la transparencia del método y la honestidad en la interpretación. En efecto, la ciencia, lejos de ser un conjunto mecánico de reglas, es una práctica profundamente ética y epistémicamente comprometida con el juicio crítico, la claridad en los límites del conocimiento y la apertura a la revisión.

Podemos pensar los métodos científicos no solo como formas de llegar a mejor a las verdades de la naturaleza, sino también como formas de mantenernos honestos y objetivos en esa búsqueda. Como explica Feynman, el cuidado que ponemos con respecto a proporcionar información completa sobre la hipótesis alternativa y posibles fuentes de error, está destinado a ayudarnos a evitar engañarnos inadvertidamente a nosotros mismos, tanto individualmente como en comunidad.

También es fundamental la comunicación honesta. Los científicos suelen añadir calificativos de diversa índole —puede ser, parece ser el caso, la evidencia sugiere— que expresan el grado de apoyo probatorio asociado a sus afirmaciones. El discurso científico está impregnado de estos marcadores de incertidumbre, que indican con precisión el nivel de confianza que puede depositarse en una determinada conclusión. Para quienes no están familiarizados con el lenguaje de la ciencia, esta forma de hablar puede parecer ambigua o indecisa. Un oyente ajeno al campo tal vez se pregunte por qué los científicos no pueden ofrecer respuestas más directas, sin ese “exceso de precaución” epistemológica. Pero tales expresiones no son un defecto del lenguaje científico: son, de hecho, una de sus virtudes fundamentales. Tienen un propósito específico en el contexto: señalar el grado apropiado de creencia que se debe atribuir a una afirmación en función de la evidencia disponible. Y tienen también un propósito más general: recordar que la ciencia no se funda en la autoridad de quien habla, sino en la solidez de la evidencia que respalda lo dicho. En este sentido, la honestidad intelectual —expresada mediante la precisión lingüística— es un componente esencial de la práctica científica. 

4.4 La honestidad científica, el gran vacío en la educación moderna  

Una conversación previsible, llena de palabras que irán chocando contra un muro sin encontrar salida. Como esos insectos que repiquetean contra los fluorescentes hasta que son abatidos por una de esas luces letales que los recibe y los convierte en un disparo. A su alrededor, todo se deshace. Las certezas se licúan como un mar incierto. Como un eco que, dentro del cerebro, va horadando un hueco hasta ocupar todo el espacio, impidiendo pensar en cualquier otra cosa.

Uno podría objetar, razonablemente, que la honestidad absoluta y la información completa no siempre pueden coexistir en la ciencia, al menos no en todas las formas detalladas que Feynman recomienda. Si bien sería útil, para el progreso del conocimiento, poder acceder a todos los datos de estudios fallidos, esto no siempre resulta factible ni deseable en la práctica. ¿Quién publicaría esos datos o los pondría a disposición, y cómo, si no es a través de publicaciones?

Todo científico activo sabe que detrás de cualquier investigación exitosa que culmina en un descubrimiento y en un artículo publicado, se esconden numerosos experimentos fallidos e hipótesis descartadas. Sin embargo, parecería poco práctico publicar sistemáticamente artículos científicos que detallen exclusivamente estos resultados negativos. A veces se dice que el secreto de la ciencia es "equivocarse rápidamente", pero eso no implica que un científico con más fracasos sea más productivo. ¿Sería económicamente viable que las revistas científicas publicaran una vasta literatura de intentos fallidos y callejones sin salida? ¿A alguien realmente le interesaría suscribirse a semejante archivo? La idea, en principio, puede parecer absurda. De hecho, es lo suficientemente provocadora como para que exista una auténtica “Revista de Resultados Irreproducibles”, dedicada a la sátira científica y al humor, que parodia precisamente esta tensión entre ideal y práctica.

Dicho esto, Feynman seguramente tiene razón en que, en muchos casos, dicha información sería útil para otros científicos e importante incluirla por las razones mencionadas: ayudar a juzgar el valor de cualquier resultado positivo que se presente. De hecho, la mayoría de los ejemplos específicos que dio Feynman involucran evidencia de hipótesis alternativas o posibles factores de confusión que un buen experimentador debería verificar como parte del proceso de prueba de hipótesis. Sería deshonesto no informar los resultados de tales pruebas. Pero es importante notar que Feynman no se limitaba a decir que sería incorrecto actuar con deshonestidad. Más bien, abogaba por un estándar positivo de honestidad, un compromiso activo con un criterio más exigente como base de la integridad científica. Integridad es la palabra clave aquí, porque la clase de honestidad radical que defendía Feynman implica precisamente la integración entre valores y métodos, tal como se requiere en la práctica ejemplar de la ciencia. Dado que el objetivo de la ciencia es responder a preguntas empíricas que satisfagan nuestra curiosidad sobre el mundo, solo mediante el esfuerzo riguroso y el máximo cuidado en los métodos y las prácticas, es posible que un científico —y la comunidad científica en su conjunto— tengan la certeza de que una pregunta ha sido respondida satisfactoriamente, y que realmente hemos alcanzado un descubrimiento genuino.

Sin embargo, esto no equivale a afirmar que deban publicarse todos los experimentos fallidos. Existen muchas hipótesis que, aunque razonables o incluso probables dado el estado actual del conocimiento, no resisten la prueba empírica; tales fracasos pueden ser valiosos e interesantes para la comunidad científica, y merecen ser publicados. Si alguien fundara una revista dedicada a ellos, seguramente encontraría una audiencia científica receptiva.

Pero otros fracasos no ofrecen valor alguno, ni por sus resultados ni por su contexto experimental. No publicarlos no es más deshonesto que no publicar estudios exitosos sin interés. Por supuesto, existen muchos casos límite, en los que el grado de interés es una cuestión de valoración editorial. Podríamos incluso coincidir en que los editores deberían adoptar una perspectiva más generosa, especialmente ahora que la publicación electrónica ha reducido considerablemente las limitaciones económicas del formato impreso.

Hay preguntas importantes que considerar, así como compromisos que evaluar en torno a la política editorial y profesional implicada. Sin embargo, en general, esta situación no constituye un verdadero contraejemplo moral a la virtud de la honestidad científica.

Hay varios puntos importantes que debemos considerar como respuesta a esta crítica de la virtud de la honestidad. El primero es distinguir entre dos cuestiones: (1) si una investigación peligrosa debe o no llevarse a cabo, y (2) si, una vez realizada, debe publicarse abierta y honestamente. La primera es una cuestión sobre los límites éticos de la curiosidad científica —por ejemplo, si el Proyecto Manhattan fue moralmente justificable—, pero no es una cuestión de honestidad en sí misma.

En el caso que nos ocupa, partimos de la base de que, por la razón que sea, la investigación ya se ha realizado. Entonces, la pregunta relevante es si no publicar los resultados (o incluso publicarlos de forma engañosa para desviar a otros) constituye una violación de la honestidad científica.

La virtud de la honestidad es central en la ciencia porque es indispensable para satisfacer la curiosidad humana a través del descubrimiento riguroso de verdades empíricas. Es una disposición práctica que hace posible la comprensión del mundo natural. Por ello, debemos asumir la honestidad como una virtud fundamental, aunque también reconozcamos que puede haber casos extraordinarios en los que su ejercicio deba sopesarse frente a otros valores éticos, como la prevención de daños públicos graves.

Lo que ocurre en tales situaciones no es que se niegue el valor de la honestidad, sino que esta se da por sentada como estándar científico, y se contrasta con otros intereses sociales de mayor alcance. El descubrimiento de la verdad es un fin importante, pero no es el único. Afirmar que la veracidad es un valor esencial en la ciencia no implica que los hallazgos científicos deban divulgarse siempre y sin excepción. A veces, hacer lo correcto puede significar retener información en un contexto social más amplio, con el fin de evitar consecuencias catastróficas.

El científico que reconoce esta posibilidad no está socavando la virtud de la honestidad, sino entendiendo que, en contextos extremos, los valores científicos pueden entrar en conflicto con valores más amplios relacionados con la seguridad o la supervivencia, y que esos conflictos requieren deliberación ética madura, no negación de principios.

A principios de la década de los 2000, Jan Hendrik Schön era una estrella en ascenso en la física. Su investigación se situaba en la intersección de la física de la materia condensada, la nanotecnología y la ciencia de semiconductores. Mientras trabajaba en los Laboratorios Bell, publicó una serie de artículos —la increíble cantidad de dieciséis como primer autor en Science y Nature, las revistas científicas más importantes del mundo— durante un periodo de dos años, presentando resultados sobre el uso de moléculas orgánicas como transistores. Uno de sus artículos fue reconocido por Science en 2001 como un “avance del año”. Recibió varios premios prestigiosos, incluido el Premio al Investigador Joven Sobresaliente de la Sociedad de Materiales. Su investigación parecía destinada a revolucionar la industria de los semiconductores, permitiendo que los chips de computadora continuaran reduciendo su tamaño más allá de los límites de los materiales tradicionales. El único problema de todo esto es que nada de eso era cierto^[4].

4.5 La lógica del método filosófico 

A menudo se piensa que la lógica juega un papel importante en la investigación científica y filosófica. Nos basamos en ella para demostrar teoremas, probar hipótesis y construir sistemas lógicos para resolver una serie de problemas. Sin embargo, a pesar de la prominencia de la lógica dentro de la investigación, tenemos una comprensión relativamente pobre de su epistemología. Por el contrario, dentro de la filosofía contemporánea de la ciencia, uno se sorprende por la amplia gama de estudios detallados sobre los mecanismos por los cuales las teorías se construyen y evalúan en las ciencias. Uno encuentra investigaciones sobre los desafíos específicos que enfrentan los modelos climáticos debido a la complejidad de su objeto de estudio^[5], y cómo los biólogos usan simultáneamente múltiples modelos para cumplir distintos objetivos predictivos y explicativos^[6]. Combinados, estos estudios pintan un panorama de la investigación mucho más complejo y multidimensional de lo que admiten las teorías confirmacionistas o falsacionistas tradicionales. Sin embargo, si bien la lógica es una actividad humana tan rica e interesante como la de las ciencias, no se pueden extraer las mismas conclusiones positivas sobre nuestra comprensión actual de su epistemología. De hecho, hasta hace poco, se habían hecho pocos intentos por elaborar descripciones detalladas de los múltiples objetivos de la lógica, los mecanismos mediante los cuales se evalúa y las fuentes de evidencia que fundamentan nuestras teorías lógicas. 

Todavía es frecuente encontrar apelaciones genéricas a las intuiciones racionales para subsanar nuestra ignorancia sobre la epistemología de la lógica. Sin embargo, no basta con reconocer nuestras deficiencias actuales. También debemos valorar cómo podemos mejorar. Primero, destacando tres supuestos que han obstaculizado el progreso de la epistemología de la lógica, y segundo, señalando (aunque sea demasiado brevemente) lo que se puede lograr una vez que evitamos estos obstáculos. Comenzamos, con el error que a veces se comete al confundir la epistemología de la lógica con la epistemología del (buen) razonamiento. 

A menudo se afirma que la lógica es el estudio del buen razonamiento, y es cierto que esta comprensión de la lógica ha desempeñado un papel importante en su desarrollo. Sin embargo, incluso si la lógica es el estudio del buen razonamiento, esto no implica que la epistemología de la lógica sea equivalente a la epistemología del buen razonamiento. Concebir la epistemología de la lógica simplemente como la epistemología del buen razonamiento ha llevado a un enfoque, a menudo singular, en especificar las condiciones bajo las cuales alguien es justificado en hacer un cierto tipo de inferencia. 

Sin embargo, una cosa es que la lógica tenga implicaciones para el buen razonamiento (deductivo), y otra es pensar que la epistemología de cómo descubrimos y justificamos estas leyes lógicas es equivalente a las condiciones bajo las cuales alguien está justificado en hacer una inferencia. Esto sería similar a reducir la epistemología de los axiomas de la aritmética a la del conteo o la suma. 

Nuestro segundo error, que es presumir que el método filosófico más adecuado para construir una epistemología de la lógica es deducirla de nuestras propias suposiciones sobre la naturaleza de la lógica, el conocimiento y la racionalidad en general. Esto se conoce como un enfoque de arriba hacia abajo para la epistemología de un campo; se parte de ciertas suposiciones (razonables) sobre el campo y otras afirmaciones que consideramos conocer, y a partir de ellas se infiere cómo debería ser la epistemología del campo dados estos hechos. 

Este enfoque ha dado lugar a muchas de las epistemologías tradicionales de la ciencia y las matemáticas, como el falsacionismo de Popper. Desafortunadamente, este enfoque suele generar imágenes simplistas de la epistemología del campo. Lo mismo ocurre con la lógica. Para corregir este error, es necesario abandonar los enfoques descendentes y adoptar un enfoque ascendente, en el que las epistemologías de la lógica se construyen a partir de estudios de caso sobre cómo los lógicos desarrollan y justifican sus teorías. En otras palabras, consideramos la práctica de los lógicos como una guía fiable de lo que constituye la epistemología de la lógica, del mismo modo que consideramos las actividades de los científicos como la guía más fiable de cómo funciona el método científico. Esta metodología, conocida como el enfoque basado en la práctica, es la base de gran parte del progreso reciente en la filosofía. 

El tercer y último error que debe evitarse, que consiste en presumir que la epistemología de la lógica debe ser completamente diferente a la de otras áreas de investigación, en particular las ciencias reconocidas. Por supuesto, dado que cada área de investigación tiene su propia temática y objetivos de investigación, esperaríamos que las normas metodológicas de cada campo reflejaran estos objetivos y las características de su temática. Sin embargo, en el caso de la lógica, la expectativa tradicional es que su epistemología sea completamente diferente a la de otras áreas, basándose en su estatus fundamental en la investigación. El resultado es una forma de fundacionalismo epistémico, en el que al menos un subconjunto de las leyes lógicas debe ser accesible de forma no inferencial para nosotros, ya sea mediante la comprensión racional o la analiticidad. Aquí mostramos que, una vez que consideramos cómo los lógicos justifican realmente su lógica, es evidente que no tenemos acceso directo a las leyes lógicas (ni siquiera de forma falible). Si bien es perfectamente aceptable proponer diferencias entre la epistemología de la lógica y las ciencias reconocidas, dichas propuestas no deberían ser axiomas basados ​​en presunciones filosóficas, sino justificarse por las realidades de la investigación en el campo. Para mostrar los beneficios de evitar estos obstáculos, es necesario una epistemología de la lógica, el predictivismo lógico, que no comete ninguno de estos errores. Según el predictivismo, las lógicas se justifican por su éxito predictivo, su poder explicativo y su compatibilidad con otros compromisos bien fundamentados. No presupone que una epistemología de la lógica sea equivalente a una epistemología del razonamiento (aunque la lógica sea, en cierto sentido, el estudio del buen razonamiento), ni que su epistemología deba ser completamente diferente a la de otras áreas de investigación (aunque seguirá teniendo sus propias características particulares), y se justifica no sobre la base de presunciones sobre cómo creemos que debería ser la epistemología de la lógica, sino más bien sobre cómo se justifican realmente las lógicas en el campo. Comprender la epistemología de la lógica es importante no solo por la vergüenza profesional que los filósofos de la lógica puedan sentir al observar los éxitos comparativos de los filósofos de la ciencia. Comprender qué hace que la lógica sea exitosa tiene claras motivaciones prácticas. A pesar del éxito de la lógica clásica, en los últimos sesenta años hemos presenciado una proliferación de lógicas no clásicas, como la paraconsistente, la subestructural y la constructivista. Cada una con sus propias motivaciones, ya sea para abordar una paradoja lógico-semántica, preocupaciones sobre la vaguedad o la naturaleza de la investigación matemática. Por supuesto, a pesar del aumento de competidores no clásicos, la lógica clásica puede ser correcta; después de todo, ha sido una teoría notablemente exitosa. Sin embargo, su éxito (y su veracidad) continuos no están asegurados. Si bien nuestro período no es precisamente uno de crisis científica, sí es uno de plenitud lógica. Con la abundancia de lógicas disponibles, tenemos la necesidad de evaluar cuál se adapta mejor a nuestros objetivos teóricos. Dado esto, al igual que durante los períodos de revolución en las ciencias, cuando la atención se centraba en cuestiones epistemológicas fundamentales sobre el campo, ahora es apropiado hacerlo con la lógica. Solo entonces podremos entender por qué algunas lógicas son mejores que otras. Sin embargo, para siquiera involucrarnos en la comprensión de estos procesos y por qué valoramos ciertas lógicas, es fundamental que prestemos a la epistemología de la lógica su propia atención, además de la del (buen) razonamiento. Por esta razón, comenzamos con una discusión de esta distinción. 

4.5.1 La epistemología de la lógica y el razonamiento

Hablar de “lógica” es ambiguo, por lo que hablar de la epistemología de la lógica está destinado a contener ambigüedades derivadas. En diferentes contextos, usamos con gusto el término “lógica” se refiere a: 

(i) el área de investigación en sí, practicada en los departamentos de filosofía, matemáticas e informática; 

(ii) los objetos, en este caso los sistemas y herramientas matemáticos, que producen los lógicos; y (iii) el/los objeto(s) de investigación del área. 

Sin embargo, inevitablemente, el uso que se haga del término influirá en la respuesta a lo que constituye la epistemología de la lógica. En particular, limitar la comprensión de la “lógica” a un tema específico dentro del área de investigación restringirá el enfoque a la epistemología de este supuesto tema. Esto ocurre a veces en los debates contemporáneos sobre la epistemología de la lógica, donde se ha prestado atención principalmente a la epistemología del buen razonamiento. Si bien este enfoque es comprensible, ya que se presupone desde hace mucho tiempo que el propósito principal de la lógica es determinar las reglas para el buen razonamiento, en última instancia limita nuestra comprensión de la epistemología de la lógica. 

Nuestro objetivo es doble. En primer lugar, advertimos contra la equiparación de la epistemología de la lógica con la epistemología de lo que a menudo se considera su objeto principal: el buen razonamiento. Si bien la lógica, correctamente entendida, es el estudio de las leyes del buen razonamiento, esto no significa que la epistemología de la lógica sea equivalente a la epistemología del buen razonamiento. Para demostrarlo, distinguimos cinco niveles de justificación “lógica”, cada uno de los cuales requiere un mayor grado de comprensión que el anterior, desde la capacidad de realizar inferencias lógicas fiables en un extremo del espectro hasta estar justificado al respaldar una lógica en el otro. Además, demostramos que las condiciones para poseer justificación en cada nivel no son suficientes para el siguiente. Por lo tanto, comprender la epistemología de cada nivel es una tarea discreta. Esto resalta la importancia de separar dos proyectos distintos: 

(i) proporcionar una epistemología para el buen razonamiento (supuestamente lógico), y 

(ii) una epistemología para la teorización lógica. 

En segundo lugar, señalamos que, para responder a preguntas importantes sobre la naturaleza de la lógica, existen razones convincentes para no restringirnos a la epistemología del buen razonamiento, sino más bien para prestar atención a formas más teóricas de justificación lógica. Esto constituye la base de nuestra decisión en centrarnos en la epistemología de la lógica entendida en este sentido más teórico: lo que llamaremos lógica artificialis. 

4.5.2  La lógica como ciencia e instrumento para el buen razonamiento 

La propuesta de que la lógica es el estudio del buen razonamiento tiene su base en el nacimiento del estudio sistemático de las reglas lógicas en la Antigua Grecia. Durante este período, la lógica abarcó una gama más amplia de temas que la lógica formal en la actualidad, incluyendo la dialéctica, la retórica y la evaluación de definiciones. Sin embargo, como es el caso ahora, la lógica se le dio la doble tarea de actuar como un instrumento para un buen razonamiento y como un área independiente de la filosofía que estudia estos principios: La lógica se originó como una ciencia para discriminar entre lo que es verdadero y lo que es falso, y para mostrar qué razonamiento realmente se adhiere al camino de la prueba argumentativa válida. Entre las diversas ramas de la filosofía, la lógica tiene dos prerrogativas: tiene tanto el honor de ser la primera como la distinción de servir como un instrumento eficaz en todo el cuerpo de conocimiento. 

Para aclarar estos roles, los filósofos en la  Edad Media introdujeron una distinción entre (i) lógica naturalis, las normas de razonamiento que los humanos realmente siguen, y (ii) lógica artificialis, las reglas establecidas por el campo de la lógica^[7]. Aunque la lógica artificialis constituía una ciencia  por derecho propio, con su propio objeto de estudio distintivo, se esperaba que las leyes que producía informaran nuestros procesos de razonamiento reales (lógica naturalis). En otras palabras, la lógica era tanto una ciencia como un instrumento. La pregunta, entonces, era hasta qué punto la lógica artificialis de la época, la silogística, cumplía con éxito esta función instrumental. 

Tanto Descartes como Bacon criticaron famosamente la lógica silogística por no ser un organon eficaz. Mientras que para Descartes, las formas eran, en el mejor de los casos, herramientas pedagógicas para quienes aún perfeccionaban sus habilidades intelectuales, no útiles para quienes ya tenían la mente clara desde el punto de vista lógico, para Bacon, las formas eran inútiles para proporcionar a los filósofos naturales los medios para hacer nuevos descubrimientos; de ahí la necesidad de un nuevo Organon^[8]. 

De manera similar, Locke criticó las formas por aportar poco a nuestra comprensión de si un argumento en particular es (in)válido. Más bien, son meras codificaciones de aquellos argumentos que ya consideramos razonables al apreciar las relaciones entre las ideas que contienen. Por lo tanto, si no se consideran razonables las instancias de las formas silogísticas desde el principio, las formas en sí mismas tendrán poca fuerza elucidatoria. Por lo tanto, si bien son correctas como codificaciones de estas inferencias aceptables existentes (el rol de la lógica como ciencia), las formas no cumplen su función instrumental. La doble función de la lógica también se evidencia en la obra de los defensores de la lógica artificialis, quienes defendían la ciencia basándose en que podía guiar eficazmente el razonamiento. Que las lógicas artificiales son necesarias para regular nuestros estándares inferenciales existentes y evitar errores innecesarios. Pues cuando el buen sentido natural emprende el análisis de un razonamiento sin la ayuda de la lógica, a veces se encuentra con cierta dificultad en cuanto a la validez de las inferencias, al descubrir, por ejemplo, que el razonamiento implica algún modo silogístico que, sin duda, es sólido, pero que no es de uso común. Así, incluso para el más ferviente defensor de la lógica formal durante este período, la lógica artificialis se reconocía como importante no solo porque constituía el estudio de argumentos correctos, sino porque servía como un instrumento eficaz para la lógica naturalis. 

Este contexto histórico es instructivo en dos aspectos. En primer lugar, nos ayuda a apreciar por qué la filosofía contemporánea concede tanta importancia al valor instrumental de la lógica para informar el razonamiento, incluso utilizando este propósito instrumental para definir el objeto de la lógica. Por ejemplo, los autores contemporáneos a menudo proponen el estudio de (una subclase de) buen razonamiento como la aplicación canónica de la lógica^[9]. Si bien los términos lógica artificialis y naturalis han salido de nuestro léxico, reemplazados por lógica formal y lógica del razonamiento, respectivamente, todavía existe la expectativa de que los frutos de la primera informen al segundo. Por lo tanto, incluso si las lógicas entendidas como cálculos matemáticos ahora se utilizan para muchos propósitos, incluido el modelado de la composición de significado^[10] y los ingresos nacionales, es común escuchar que la aplicación filosóficamente primaria de nuestras lógicas (los productos de la lógica artificialis) es el razonamiento, lo que nos permite identificar el razonamiento que es lógicamente bueno o, para abreviar, "lógico". 

En segundo lugar, reconocer este doble papel de la lógica artificialis como ciencia propia y como instrumento de razonamiento explica en cierta medida cómo se han producido equívocos de la “epistemología de la lógica”, aplicándose el adjetivo “lógico” por igual a aquellos razonamientos en lenguaje natural que las lógicas formales supuestamente sancionan. Por ejemplo, la inferencia de «Iré a Morelia este fin de semana» sobre la base de «Iré a Zamora o a Morelia este fin de semana» y «No volveré a ir a Zamora» se considera lógica porque está sancionada por la regla (supuestamente válida) del silogismo disyuntivo expresada por las lógicas formales. Este equívoco se hace patente cuando se habla de “inferencias lógicas”, que pueden utilizarse para referirse por igual a las reglas de implicación dentro de una lógica y a inferencias particulares realizadas dentro del lenguaje natural sancionadas por estas reglas. Así, el adjetivo (y honorífico) “lógico” ha llegado a representar ambiguamente los principios de la lógica y las instancias de razonamiento a las que estos principios se aplican. Esta ambigüedad puede tener consecuencias desafortunadas para la epistemología de la lógica.

4.5.3 Equiparar la epistemología de la lógica con la del razonamiento lógico

La epistemología de la lógica se pregunta:

• ¿Cómo justificamos nuestras creencias lógicas (por ejemplo, la ley de no-contradicción es verdadera)?
• ¿Qué tipo de conocimiento es el conocimiento lógico: a priori, empírico, conceptual, convencional o práctico?
• ¿Cómo explicamos el desacuerdo lógico entre sistemas (clásico, intuicionista, paraconsistente)?

La intuición racional es la facultad mediante la cual la mente capta de manera directa y evidente una verdad racional, sin necesidad de razonamiento discursivo. Axiomas lógicos o matemáticos: se consideran conocidos de forma inmediata por intuición racional. Epistemología del a priori: cómo es posible el conocimiento independiente de la experiencia. Filosofía analítica y ética: cuando se apela a intuiciones morales o conceptuales para fundamentar juicios racionales.

Una consecuencia de equiparar la lógica con el estudio del buen razonamiento es que las discusiones sobre la epistemología de la lógica se deslizan fácilmente hacia la epistemología del buen razonamiento. Especificar la epistemología de la lógica se convierte simplemente en especificar la del buen razonamiento: bajo qué condiciones un individuo razona de manera confiable, lógicamente hablando, o bajo qué condiciones un individuo está justificado para hacer inferencias (supuestamente lógicas). Esto ha llevado a una diferenciación insuficiente entre los requisitos necesarios para estar justificado al hacer una inferencia particular (supuestamente lógica) y los necesarios para estar justificado al proponer una lógica. La epistemología de la lógica artificialis se ha equiparado con la de la lógica naturalis o se ha ignorado como el costo de enfocarse en esta última. Un ejemplo del primer problema se ilustra en el caso de BonJour sobre la indispensabilidad de la intuición racional para la justificación epistémica. En lo que respecta a la justificación lógica, BonJour aborda la necesidad de la intuición racional para justificar de golpe las inferencias (lógicas) y nuestras creencias sobre las leyes lógicas^[11]. La intuición racional es necesaria para explicar nuestro éxito al hacer inferencias a partir de conjuntos de premisas hasta una conclusión, ya que ni la justificación empírica ni la analiticidad pueden explicar la justificación inferencial. Sin embargo, BonJour plantea exactamente el mismo punto sobre la justificación de ciertas leyes lógicas, como la ley de no contradicción. Nuestra justificación para estas leyes no puede provenir plausiblemente de fuentes empíricas ni de la analiticidad; solo la intuición racional será suficiente. Por lo tanto, no se hace ninguna diferenciación entre los requisitos epistémicos para razonar (lógicamente) y estar justificado al creer en las leyes lógicas. Ambos se adquieren directamente a través de la intuición. De hecho, BonJour se mueve libremente entre hablar sobre la necesidad de la intuición racional para justificar inferencias y leyes lógicas: “Cuando considero cuidadosa y reflexivamente la proposición (o inferencia) en cuestión, puedo simplemente ver, captar o aprehender que la proposición es necesaria, que debe ser verdadera en cualquier mundo o situación posible (o alternativamente, que la conclusión de la inferencia debe ser verdadera si las premisas son verdaderas)”. Sin embargo, no hay razón para asumir que las condiciones bajo las cuales estamos justificados para hacer inferencias de cierto tipo deben ser las mismas que determinan cuándo estamos justificados para creer en los principios que las sancionan. Por supuesto, pueden resultar ser las mismas, pero no separar ambos asuntos nos impide abordar adecuadamente la cuestión. En otras ocasiones, interpretar la epistemología de la lógica como la epistemología del razonamiento (exitoso) se ejemplifica como una omisión total de cómo justificamos nuestras mejores teorías lógicas, como en el intento de Schechter de proporcionar una explicación naturalista de la justificación del “pensador ordinario” de la lógica en términos de selección natural^[12]. Para Schechter, la epistemología de la lógica “tiene dos tareas explicativas principales: explicar cómo nuestras creencias lógicas son fiables y cómo somos epistémicamente responsables de creer como lo hacemos”. Sin embargo, aunque Schechter habla explícitamente de creencias lógicas en lugar de inferencias, no le preocupa cómo llegamos a determinar las leyes lógicas correctas (es decir, cuestiones de lógica artificialis). Más bien, le preocupa cómo los individuos llegan a deducir de forma fiable y, en consecuencia, a creer en afirmaciones cotidianas del lenguaje natural, como ”Toda mosca es una mosca”, que la lógica correcta (sea cual sea esta última) considera lógicamente verdaderas. En otras palabras, Schechter se ocupa exclusivamente de la fiabilidad de la lógica naturalis. Aquí, la epistemología de las principales tareas de la lógica se concibe de forma que se centre exclusivamente en la fiabilidad de la lógica naturalis, omitiendo cualquier consideración de cómo llegamos a estar justificados al creer en la lógica correcta que sanciona estas prácticas inferenciales. 

Un ejemplo más complejo e instructivo es la explicación naturalista alternativa de la lógica de Maddy, que es simultáneamente un proyecto metafísico que proporciona una explicación de lo que fundamenta los hechos lógicos y una teoría de cómo llegamos a creer de forma fiable en las verdades lógicas resultantes^[13]. En ambos casos, en consonancia con los principios naturalistas, Maddy pretende trabajar desde "dentro de la ciencia", utilizando sus métodos y las mejores teorías actuales. La respuesta de Maddy a la pregunta metafísica es que los hechos lógicos se fundamentan en las características estructurales del mundo. Específicamente, nuestro mundo exhibe una estructura KF (abreviatura de estructura Kant-Frege), lo que significa que "consiste en un dominio de objetos que tienen propiedades y se encuentran en relaciones, quizás algunas propiedades universales, más compuestos de estas que involucran conjunciones, disyunciones y negaciones, y [que] algunas interconexiones entre estas situaciones son dependencias robustas consecuentes del terreno". Lo que resulta de estas estructuras KF es la verdad de una "lógica rudimentaria", con similitudes con la lógica fuerte de Kleene con lagunas de valores de verdad. La pregunta epistemológica se responde entonces proponiendo que los individuos son adecuadamente sensibles a estos hechos lógicos en virtud de su aparato cognitivo que les permite "detectar y representar" estas características estructurales del mundo. El panorama general es audaz y atractivo. Proporciona una explicación de la lógica que mantiene su objetividad sin apelar a un tercer reino platónico. Sin embargo, existe una ambigüedad en la obra de Maddy sobre el tema de esta justificación “lógica”, que impacta la epistemología resultante. ¿Esta sensibilidad a los hechos lógicos nos proporciona las leyes de la lógica que constituyen nuestras mejores teorías lógicas, o simplemente permite a los individuos adoptar prácticas inferenciales confiables que les brindan creencias que resultan ser (lógicamente) verdaderas? En otras palabras, ¿le preocupa a Maddy proporcionar una epistemología de la lógica artificialis o una explicación de la confiabilidad de la lógica naturalis? A veces, Maddy tiene claro que se trata de esto último: “las verdades lógicas que tengo en mente son los ejemplos más simples e incontrovertibles”, como «Si todos los robles son árboles y este es un roble, entonces este debe ser un árbol». Por lo tanto, más que leyes lógicas, a Maddy le preocupa cómo los individuos llegan a formar creencias confiables (lógicamente correctas), como Schechter. Sin embargo, al mismo tiempo, Maddy también parece interesada en explicar cómo, dado que la lógica rudimentaria es cierta en nuestro mundo, llegamos a respaldar la lógica clásica. Una pregunta que no tiene nada que ver con la fiabilidad de la lógica naturalis, sino más bien con lo que justifica nuestra aprobación de nuestra mejor teoría lógica (que se presume es la lógica clásica). La propuesta de Maddy es que la lógica clásica es una idealización de la lógica rudimentaria, a la que se llega al suponer que cada predicado tiene un límite definido, que todos los nombres se refieren a ella y que el condicional se comporta de manera veritativo-funcional en lugar de representar causalidad. Claramente, ahora hemos pasado a la cuestión epistemológica distinta de qué justifica nuestra aprobación de una lógica particular; una epistemología de la lógica artificialis. Sin embargo, como epistemología de la lógica artificialis, es insuficiente. No se nos proporcionan detalles de cómo descubrimos y finalmente llegamos a estar justificados en creer en esta teoría (idealizada) de los hechos lógicos. ¿Qué es lo que justifica nuestra aprobación de la lógica clásica, en lugar de, digamos, una lógica constructivista?

La lógica constructivista parte de la idea de que solo existen las entidades matemáticas que pueden construirse efectivamente. En lugar de aceptar que una proposición es verdadera o falsa independientemente de que lo sepamos, sostiene que: “Una proposición es verdadera solo si podemos demostrarla constructivamente.” La verdad equivale a demostrabilidad y la negación de una proposición significa que “suponerla conduce a una contradicción”. El sistema formal más conocido de lógica constructivista es la lógica intuicionista desarrollada por Heyting, quien formalizó las ideas de Brouwer. Su cálculo proposicional y de predicados se parece al clásico, pero con reglas modificadas para evitar el uso del tercero excluido. Es la base lógica de la teoría de tipos y de la correspondencia de Curry–Howard, que vincula demostraciones con programas computacionales: “Demostrar es construir un programa; la verdad es su ejecución exitosa.”

La respuesta no puede ser simplemente que la lógica clásica es una representación fiel, aunque idealizada, de los hechos lógicos entregados por las estructuras de nuestro mundo KF. Esto simplemente nos dice qué hace que la lógica clásica (idealizaciones aparte) sea verdadera, no cómo llegamos a estar justificados en creerla. El hecho de que la ley de Avogadro refleje con precisión hechos sobre la naturaleza de los gases no es lo que justifica nuestro compromiso con la ley. Esto podría explicar qué la hace verdadera, pero no cómo llegamos a estar justificados en creer en la ley en primer lugar. En un momento, Maddy parece explicar nuestra justificación para respaldar la lógica clásica sobre la base de que es una idealización de la lógica rudimentaria, que no solo es "verdadera del mundo" sino que también "está incrustada en nuestros modos más primitivos de cognición y representación". Sin embargo, dejando de lado que se supone que la lógica clásica es una idealización de los hechos lógicos, un proceso que requiere una teorización compleja, el hecho de que ciertos principios estén arraigados en nuestros modos de cognición y representación no basta para explicar cómo llegamos a creer justificadamente en una teoría que expresa estos principios. Después de todo, aunque las reglas gramaticales de mi lengua materna puedan estar arraigadas en mi área de Broca, esto no significa que estas reglas me resulten claras. De hecho, es improbable que lo sean. De lo contrario, no necesitaríamos la lingüística descriptiva para descubrir estas reglas; simplemente podríamos preguntar directamente a los hablantes nativos cuáles son las reglas gramaticales. Por lo tanto, incluso si admitimos que el hecho de que estos principios de lógica rudimentaria estén arraigados en nuestros modos de cognición explica (parcialmente) cómo llegamos a hacer inferencias (lógicas) fiables sobre el mundo, no explica cómo llegamos a creer justificadamente en cuáles son estos principios. En general, ser sensible a un conjunto de hechos o reglas que determinan la práctica competente y garantizar su cumplimiento no garantiza el acceso consciente a estos hechos o reglas constitutivas. En particular, si la sensibilidad a los hechos lógicos fuera suficiente para justificar su creencia, tendría sentido afirmar que los matemáticos expertos estaban justificados al creer en los principios de la lógica clásica de primer (o segundo) orden antes del siglo XX porque exhibían la capacidad de razonar de acuerdo con ellos en sus demostraciones. Sin embargo, no fue así. Para ello, se requirió el ingenio de Frege, Russell y Whitehead. Siempre que existe un conjunto de principios relacionados con el desempeño competente de los individuos en una tarea, la epistemología de los principios correctos que dictan dicha práctica es distinta de las condiciones epistémicas de la propia práctica competente. Esto se aplica al uso del lenguaje, a la aritmética y a la lógica. Un hablante de inglés puede ser perfectamente consciente de que la frase «The black huge dog» suena mal mientras que «The huge black dog» suena bien, sin saber por qué. De manera similar, la competencia en inferencia no implica una conciencia reflexiva de las leyes (lógicas) que constituyen esta competencia. Estos breves ejemplos resaltan los peligros de distinguir inadecuadamente entre una epistemología de buen razonamiento lógico (lógica naturalis competente) y teorización lógica (lógica artificialis). Esto puede llevarnos a omitir por completo la consideración de esta última o a presumir que una respuesta a esta última se sigue directamente de la primera. Ahora avanzamos en nuestro punto, mostrando que hay (al menos) cinco niveles distintos de justificación "lógica", cada uno aumentando en sofisticación y comprensión con respecto al anterior; algunos relacionados con ser un razonador confiable, otros con obtener justificación para los principios lógicos correctos. Dado que las condiciones para poseer cada nivel son distintas, esto muestra además la necesidad de distinguir una epistemología de la lógica artificialis de los requisitos epistémicos para ser un razonador (lógico) confiable.

4.6 Cinco “niveles” de justificación lógica

Nivel 1: Competencia lógica. 

Realizar inferencias (lógicas) de forma fiable. En el nivel más rudimentario de la justificación lógica se encuentra la capacidad de inferir de forma fiable de acuerdo con los estándares considerados lógicos. El individuo que posee esta justificación puede razonar desde «Tendré que pagar una multa si no pago el aparcamiento» y «No quiero que me multen» hasta la conclusión de que mejor paga el aparcamiento. Lo que no se requiere para este nivel de justificación es una creencia proposicional consciente de que estas inferencias relevantes son buenas (y mucho menos válidas). Tampoco se exige que el individuo sea sensible a cualquier distinción entre inferencias lógicas y no lógicas, suponiendo que exista una. Esta forma de justificación (lógica) es similar a la competencia lingüística que esperamos de los hablantes nativos. Su justificación consiste en ser capaz de participar de forma competente en una práctica sancionada por un conjunto de reglas tácitas. Debido a la naturaleza puramente práctica de esta forma de justificación, sin ninguna creencia consciente asociada, algunos podrían dudar en llamarla simplemente justificación. De hecho, dado que no se exige que el agente tenga acceso a las razones por las que las inferencias relevantes son aceptables, es más apropiado llamar a este nivel de justificación lógica una instancia de garantía, en lugar de justificación en sentido técnico. Al igual que con la competencia lingüística, se dice que nuestro agente posee garantía para estas actividades inferenciales en virtud de su fiabilidad al realizar dichas inferencias de acuerdo con las leyes de implicación correctas.

Los requisitos exactos para esta forma rudimentaria de garantía son un tema candente en la epistemología del razonamiento. Después de todo, no cualquier transición mental de un estado cognitivo a otro suele considerarse una inferencia. Una creencia nuestra permanente puede simplemente hacer que forme una nueva creencia, por asociación libre o condicionamiento programado, y normalmente desearíamos distinguir estos casos de aquellos en los que se infiere una nueva creencia a partir de otras. Un medio común para diferenciar los meros movimientos mentales de las inferencias es exigir que el movimiento en este último caso esté causado por un reconocimiento asociado de que las creencias establecidas respaldan la nueva creencia, lo que Boghossian llama la condición de toma: para que alguna R constituya una inferencia en alguna circunstancia doxástica C, entonces la propia R debe explicarse en parte por la toma de algunos elementos de C para justificar su R^[14]. Determinar si se requiere cumplir la condición de toma o algo similar para que cuente como hacer una inferencia (lógica) es innecesario para nuestros propósitos. No nos interesa proporcionar una epistemología completa del razonamiento. Todo lo que requerimos es que, en primer lugar, ser capaz de hacer una inferencia lógica de manera confiable no implica que uno esté justificado en creer en los principios que determinan esta confiabilidad y, en segundo lugar, que cumplir la condición de toma no requiera una actitud consciente hacia aquellos argumentos que representan las inferencias que se están haciendo. El primer requisito lo cumplen claramente la mayoría de los razonadores fiables, y el segundo quienes carecen del deseo o la capacidad de reflexionar conscientemente sobre su práctica inferencial (incluidos los niños). 

Nivel 2: Buena práctica consciente. 

Creencia justificada de que algunas proposiciones se derivan de otras. Esto nos lleva al segundo nivel de justificación lógica, la Buena Práctica Consciente, que requiere que un agente tenga actitudes conscientes hacia el conjunto relevante de proposiciones. Este nivel de justificación lo alcanza un agente, en primer lugar, al reflexionar conscientemente sobre sus actividades inferenciales, de modo que no solo asume algunos estados doxásticos preexistentes para respaldar uno nuevo, sino que considera válido el argumento asociado que representa la inferencia. En segundo lugar, aprecia que el argumento asociado no es simplemente válido, sino que las proposiciones que expresan las creencias preexistentes (las premisas) garantizan la proposición que expresa la nueva creencia (la conclusión). En otras palabras, puede diferenciar con fiabilidad entre argumentos en los que las premisas simplemente respaldan la conclusión y aquellos en los que las premisas la garantizan.

Sin embargo, si bien existe sensibilidad para distinguir entre argumentos deductivamente y no deductivamente buenos, no la hay para diferenciar entre inferencias lógicas y no lógicas, ni para determinar si un argumento es bueno por razones lógicas. Por lo tanto, nuestro individuo con Buenas Prácticas Conscientes no tiene forma de diferenciar la implicación de «Llegaré tarde al trabajo si mi coche se avería» y «mi coche se ha averiado» de «Llegaré tarde al trabajo», que a menudo se considera una implicación lógica, y las implicancias léxicas no lógicas estándar como «Juan fue asesinado», por lo que «Juan está muerto». En ambos casos, para nuestro individuo, la conclusión parece simplemente derivarse de la(s) premisa(s). De hecho, si bien existe evidencia de la ciencia cognitiva que indica que los razonadores cotidianos pueden diferenciar entre inferencias no deductivas y deductivas^[15], no hay ninguna que sugiera que posean una apreciación similar para la distinción entre inferencias deductivas lógicas y no lógicas. Esto último solo surge en niveles más teóricos de comprensión, cuando se construyen sistemas formales para explicar la bondad de estas inferencias. Relacionado con esto, en este nivel, aún no se aprecia por qué exactamente estos argumentos son buenos; simplemente que lo son. Explicar por qué un argumento es bueno requiere especificar las consideraciones relevantes que diferencian los buenos argumentos de los malos. 

Nivel 3: Buena justificación del esquema. 

Creencia justificada de que algunas proposiciones se siguen de otras, basada en características estructurales. Aquí tenemos no solo la creencia justificada de que un argumento es bueno, sino también cierta sensibilidad a las razones del porqué; razones comúnmente asociadas con la logicidad. Específicamente, que hay ciertas características estructurales del argumento que explican su bondad. Por ejemplo, que la inferencia a "Iré a Marsella este fin de semana" sobre la base de "Iré a Herne Bay o a Marsella este fin de semana" y "No volveré a Herne Bay" es buena porque ejemplifica la forma "O P o Q, pero no P, y por lo tanto Q". Incluso puede existir cierta conciencia de que estas características estructurales son compartidas por múltiples argumentos, que son aceptables conjuntamente en virtud de poseerlas. Reconocer este hecho es el punto de partida de la lógica formal: que un argumento es bueno en virtud de su forma (en cierto sentido). Este nivel de justificación lógica es similar al tipo de reflexión gramatical intuitiva común entre los usuarios de lenguas cuando intentan dar sentido a sus intuiciones lingüísticas, impulsados ​​por la pregunta de un niño o un caso complejo. Por ejemplo, al usar verbos modales en una pregunta, el verbo siempre precede al sujeto (¿Puedo tomar prestado esto? en lugar de ¿Puedo tomar prestado esto?). Esta reflexión presupone que, aunque las reglas gramaticales no nos resulten transparentes, existen reglas pertinentes que determinan si una oración en la lengua tiene sentido o no. De igual manera, si bien no es necesario que tengamos a mano las reglas que dictan los estándares inferenciales aceptables, sí existe, no obstante, un conjunto de principios que rigen la corrección de nuestras actividades inferenciales. Si bien la justificación de un buen esquema se distingue del nivel anterior en términos de su sensibilidad hacia algunos de los factores que hacen que un argumento sea bueno, aún faltan elementos importantes que la diferencian del nivel de comprensión teórica deseado en la lógica contemporánea. En primer lugar, el reconocimiento de que algunos argumentos son buenos debido a sus características estructurales no es suficiente para diferenciar las implicaciones lógicas de las no lógicas. Después de todo, las implicaciones no lógicas pueden ejemplificar una estructura léxica que explica su validez. Esta diferenciación entre consideraciones lógicas y no lógicas solo ocurre a un nivel más teórico, cuando se postulan conectores lógicos dentro de una lógica para explicar por qué los conjuntos de argumentos son buenos. En segundo lugar, aún no se aprecia por qué los argumentos de estas formas son buenos. Más bien, todo lo que tenemos son generalizaciones sobre argumentos en forma de esquemas, a las que se llega mediante la abstracción de argumentos específicos considerados aceptables. Sin embargo, las generalizaciones no necesariamente constituyen explicaciones en sí mismas. La generalización «Todos los cisnes son blancos» no nos dice por qué los cisnes son de ese color, solo que lo son. De manera similar, identificar que los argumentos de una forma dada son buenos no necesariamente nos dice por qué ejemplificar esta forma los hace buenos; simplemente que lo son. Puedo apreciar que todo argumento de la forma “O P o Q, pero no P, y por lo tanto Q” es bueno, sin tener idea de por qué. Específicamente, podría no ser capaz de explicar por qué los argumentos de esta forma son buenos, pero no puede decirse lo mismo de los argumentos de la forma “P si Q, P, y por lo tanto Q”. Por supuesto, esto no significa que comprender las características estructurales de los argumentos sea inútil. Hay una distinción importante que debe hacerse entre heurísticas predictivamente útiles y modelos genuinamente explicativos. Ser consciente de estas características estructurales mediante la abstracción puede tener éxito regulan nuestras actividades inferenciales y actitudes hacia los argumentos hasta cierto punto, y por lo tanto tienen valor predictivo, sin explicar por qué son buenos. Por razones relacionadas, aún no se reconoce la validez de estos argumentos. La validez es un concepto técnico que postulan nuestras teorías lógicas para explicar por qué.

Un argumento es bueno, ya sea en términos de teoría de modelos, teoría de pruebas u otros. El uso efectivo del concepto requiere ir más allá del mero reconocimiento de que los argumentos son buenos debido a sus características estructurales; requiere que seamos capaces de explicar qué diferencia las formas que son buenas de las que no lo son. Esto nos lleva a una última diferencia entre la justificación de un buen esquema y niveles teóricos más profundos. Los principios intuitivos que se extraen sobre las formas "buenas" de argumentación en este nivel todavía se formulan dentro de un lenguaje casi natural reglamentado, no en los lenguajes artificiales definidos con precisión de la lógica moderna. Por lo tanto, comprender los esquemas que determinan la bondad intuitiva de los argumentos presupone una comprensión del lenguaje objeto existente y, por lo tanto, de los argumentos en lenguaje natural que instancian estas formas. Esto significa que usar estos esquemas para demostrar que un argumento dado es bueno sufrirá las preocupaciones históricamente planteadas contra la lógica silogística. A menos que haya fallos de memoria o que el argumento en particular sea difícil de analizar, estar informado del principio esquematizado "bueno" no revelará nada que no se haya podido apreciar ya con solo observar el argumento específico. Si uno no ve ya que "Iré a Marsella este fin de semana" se sigue de "Iré a Herne Bay o a Marsella este fin de semana" y "No volveré a Herne Bay", difícilmente se convencerá si se le dice que es una instancia de "O P o Q, pero no P, y por lo tanto Q". Después de todo, para apreciar que ejemplificar este esquema basta para que el argumento sea bueno, se requiere reconocer la bondad de los argumentos específicos que (supuestamente) instancian el esquema en primer lugar. La esquematización es simplemente una generalización universal sobre las instancias del argumento; o ya acepté que el argumento era bueno, o tendré mis dudas sobre el supuesto "buen esquema". La posibilidad de explicar por qué las oraciones del lenguaje objeto implican a otras, sin presuponer la comprensión de los argumentos, deberá esperar hasta que se construya un lenguaje formal con su propia semántica. Por lo tanto, si bien el agente que posee una buena justificación de esquema posee un grado de reflexión sobre sus actividades inferenciales (logica naturalis) y, por lo tanto, un nivel de dominio regulado de dichas inferencias que no se encuentra en niveles anteriores, no alcanza la justificación que buscamos en la lógica contemporánea. 

Nivel 4: Justificación de leyes lógicas. 

Creencia justificada de que algunas reglas lógicas son válidas. Ahora pasamos al nivel de justificación teórica que se obtiene al tomar un curso introductorio de lógica o matemáticas discretas. Aquí, el agente comprende la presuposición básica de la lógica formal —que existen estructuras subyacentes que determinan la validez de un argumento— y aprecia los lenguajes formales pertinentes (ya sean proposicionales, de primer orden o superiores).

La distinción entre vocabulario lógico y no lógico, y el concepto de VALIDEZ. Además, habrán aprendido algunas reglas lógicas, como el modus ponens, el silogismo disyuntivo y la reductio vitae, que desempeñan un papel importante en nuestras prácticas inferenciales. Si se les presiona, incluso podrían demostrar la validez de un argumento utilizando las herramientas que se les proporcionan, ya sean tablas de verdad, teoría de modelos o deducción natural. En este sentido, se puede decir que son capaces de proporcionar una explicación rudimentaria de la validez de un argumento específico en lenguaje natural: cuando se formaliza adecuadamente, se demuestra la conclusión a partir de sus premisas utilizando únicamente las reglas aceptables de la lógica, y así sucesivamente. Sin embargo, aún falta comprender por qué estas reglas formales son las que dictan la validez y no otras, por qué la validez se define de esta manera y no de otra, y por qué se utiliza este lenguaje formal específico y no otros. En otras palabras, lo que falta es una apreciación de lo que justifica los postulados teóricos que se les enseñan en primer lugar. 

Nivel 5: Justificación de la elección de teoría. 

Creencia justificada de que cierta lógica L es la lógica correcta de validez. Esto nos lleva al nivel más profundo de la justificación lógica, donde el agente está justificado al creer que una lógica particular es verdadera. Aquí, la justificación que se posee va más allá de la del nivel anterior en virtud de la conciencia de lo que justifica la elección de la lógica: por qué, por ejemplo, deberíamos adoptar una lógica que valide el silogismo disyuntivo, por qué deberíamos usar un lenguaje de primer orden en lugar de uno de orden superior, etc. Ser consciente de lo que justifica una elección de lógica requiere que el agente tenga cierta sensibilidad a lo que constituye evidencia adecuada para dicha lógica. Del mismo modo, un científico que es consciente de lo que justifica la elección entre teorías en competencia debe ser sensible a lo que constituye evidencia adecuada para dichas teorías. Esto no significa, por supuesto, que el individuo tenga una comprensión reflexiva detallada de lo que constituye evidencia para una lógica; simplemente significa que es sensible a estas razones. Poseer una comprensión reflexiva completa de la metodología de estas decisiones es algo que solo esperamos en el ámbito de la filosofía de la lógica. Cabe destacar que, salvo a través del testimonio, muchos filósofos carecen de una justificación de este tipo. Es decir, ser capaces de explicar por qué la lógica clásica es mejor que la intuicionista o una lógica relevante, por ejemplo, o por qué deberíamos definir la validez en términos de teoría de modelos en lugar de teoría de pruebas. De hecho, la característica definitoria de la justificación de la Teoría de la Elección —que el agente tiene acceso a las razones por las que es racional avalar una lógica particular sobre otras— garantiza que dentro de este nivel habrá infinitas gradaciones de justificación. Se podrían conocer los argumentos a favor de la lógica clásica, pero ignorar las debilidades destacadas por los programas de investigación no clásicos. Además, se podrían conocer los desafíos que plantea la lógica intuicionista, pero no los de la lógica subestructural, y así sucesivamente. En este sentido, poseer una justificación de la Teoría de la Elección dentro de la lógica no difiere de la que se obtiene dentro de las ciencias; El grado de este nivel de justificación dependerá de la pericia y experiencia en el campo. Es importante destacar que alcanzar este nivel de justificación requiere más que estar informado sobre la lógica convencional actual. Es necesario realizar investigación lógica. Solo así se puede comprender por qué ciertas opciones teóricas son mejores que otras y por qué algunas lógicas son preferibles a otras. Alcanzar este nivel de comprensión y justificación constituye un objetivo de la lógica contemporánea. Por lo tanto, comprender cómo los lógicos alcanzan este nivel de comprensión puede considerarse uno de los objetivos de una epistemología de la lógica artificialis.

4.7 La epistemología de la lógica artificial

Claramente, entonces, se puede poseer competencia lógica sin justificación de la elección teórica. La mayoría de las personas serán razonadores fiables sin llegar a creer justificadamente que el modus ponens es válido, y mucho menos que la lógica clásica es correcta. La competencia lógica (de razonamiento) no es peculiar en este sentido. Es normal ser competente en una práctica sin tener justificación para creer en los principios que determinan dicha competencia. Se puede ser bastante hábil en aritmética sin saber absolutamente nada sobre los axiomas de la aritmética de Peano. En consecuencia, comprender las condiciones bajo las cuales alguien se convierte en un profesional competente es distinto de comprender cómo un individuo obtiene acceso epistémico a esos principios que dictan la competencia. Específicamente, una epistemología de la inferencia (lógica) fiable no nos proporcionará directamente una perspectiva de cómo llegamos a creer justificadamente en una lógica (lógica artificialis). 

La mera sensibilidad a los hechos lógicos (si los hay) no basta para explicar cómo llegamos a construir y probar las teorías (lógicas) que ahora aceptamos, ni cómo demostramos que son mejores que las de la competencia. Así pues, incluso si, en última instancia, el valor de la lógica artificialis reside en su capacidad para dilucidar las reglas que regulan adecuadamente la lógica naturalis, determinar la epistemología de la lógica artificialis no equivale a determinar las condiciones para un razonamiento (lógico) fiable. Concedido, entonces, que proporcionar una epistemología del razonamiento (lógico) fiable no basta para una epistemología de la teorización lógica. Pero ¿por qué preocuparse por esto último? ¿Por qué esforzarse por una epistemología de la lógica artificialis? No solo nos consideramos razonadores fiables. Construimos lógicas para demostrar por qué ciertas afirmaciones siguen a otras, y al hacerlo, consideramos que sancionamos muchas de las inferencias en las que se basan los matemáticos y científicos. Sin embargo, presumiblemente, no creemos que nuestra elección de lógica sea arbitraria; algunas teorías son mejores que otras. Los lógicos clásicos rara vez admiten que su elección de lógica se basa en el gusto personal. 

¿Qué justifica su conclusión? ¿Por qué pensar que estamos racionalmente justificados para respaldar una lógica específica y que alguna lógica L1 es mejor que otra L2? Solo una epistemología adecuada de la lógica artificialis puede proporcionar una respuesta. Además, estas preguntas están íntimamente ligadas a otros temas importantes dentro de la filosofía de la lógica, como hasta qué punto la epistemología de la lógica es similar a la de las ciencias reconocidas  y si, a diferencia de los desacuerdos en otras áreas de investigación, los desacuerdos sobre la lógica son inherentemente irracionales^[16]. De nuevo, solo una epistemología de la lógica artificialis puede abordar estas cuestiones. Una epistemología informativa de la lógica artificialis no debería limitarse a comprender el pasado. Sí, debería ayudarnos a comprender por qué fue racional pasar de la lógica silogística a la clásica, por ejemplo. Pero también podría ayudarnos a comprender cómo podemos mejorar nuestras teorías en el futuro. Al comprender con mayor precisión los criterios para una lógica exitosa, deberíamos ser capaces de apreciar mejor las oportunidades para mejorar nuestras teorías actuales. Al igual que en las ciencias, deberíamos creer que un profesional de la lógica más reflexivo metodológicamente es un profesional más eficaz. Estas consideraciones muestran que poseer una epistemología de la lógica artificialis ofrece beneficios significativos, lo cual no podría lograrse únicamente mediante una epistemología del buen razonamiento (lógico). Sin embargo, por el momento, estas son solo promesas audaces, un manifiesto electoral. Cumplirlas requiere que utilicemos el método filosófico correcto para investigar la lógica artificialis. La falta de una metodología apropiada es una razón más por la que aún no poseemos una epistemología de la lógica plenamente desarrollada, a diferencia de lo que ocurre en las ciencias. 

4.8 El enfoque basado en la práctica

Argumentamos que sería un error asimilar la epistemología de la lógica con la del buen razonamiento. Comprender plenamente la epistemología de la lógica requiere ir más allá de las cuestiones de qué constituye nuestra justificación para hacer inferencias (lógicas) específicas, a qué justifica nuestra elección de lógica y afirmaciones sobre estas lógicas. Nuestra siguiente pregunta, entonces, es: ¿Cómo abordamos esta epistemología de la lógica artificialis? Aquí, nos ocupa la metodología filosófica; ¿qué método deberían usar los filósofos para descubrir la epistemología de algún dominio? Al intentar comprender la epistemología de un dominio, ya sea matemático, científico o conocimiento perceptivo cotidiano, puede existir la tentación de dejarse llevar por lo que esperamos que sea el conocimiento de este tipo o qué propiedades debería poseer el conocimiento dentro de este dominio. Además, podemos ser impulsados ​​por el deseo de resolver enigmas epistémicos específicos con respecto a estos tipos de conocimiento, provocados por preocupaciones escépticas generales o nuestros propios compromisos filosóficos. En estos casos, el objetivo es proporcionar una epistemología del dominio que respete las propiedades que deseamos asignarle, evitando al mismo tiempo posibles consecuencias negativas. Este enfoque ha sido históricamente común en la filosofía de la ciencia. El rechazo de Popper (1959) al verificacionismo y la defensa del falsacionismo no se basaron en conclusiones extraídas de estudios de caso detallados sobre la elección de teorías científicas, sino en la percepción de amenazas al conocimiento científico. En primer lugar, existían teorías que se presentaban como científicas, pero que no cumplían con los estándares requeridos para ser propiamente científicas. Dado que otorgar a estas teorías pseudocientíficas el mismo estatus que a las ciencias podría tener consecuencias sociales negativas, era importante que se discriminaran claramente. Este era un requisito que el verificacionismo no podía cumplir, dado que es demasiado fácil encontrar evidencia favorable para cualquier teoría, científicamente correcta o no. En segundo lugar, solo el falsacionismo (supuestamente) podía evitar el uso de inferencias inductivas dentro de la actividad científica y, por lo tanto, las conclusiones escépticas derivadas del problema de Hume. Una historia similar puede contarse para algunas epistemologías de las matemáticas. La explicación racionalista de Katz de la justificación matemática en términos de la intuición no está motivada por una consideración detallada de las formas de evidencia que los matemáticos proporcionan para sus afirmaciones, sino por el deseo de explicar cómo es posible el conocimiento sobre las matemáticas manteniendo un compromiso con el realismo sobre los objetos matemáticos abstractos. El compromiso con los objetos matemáticos abstractos en sí mismo ha sido motivado por una insatisfacción con las alternativas antirrealistas. Estas propuestas ejemplifican un enfoque descendente de la epistemología de un dominio. Se comienza con ciertos criterios de éxito para lo que la epistemología de el dominio debería ser similar. Esto puede incluir evitar un desafío escéptico particular, respetar las expectativas del autor respecto a la metafísica del área, cumplir con supuestos epistemológicos específicos establecidos sobre la racionalidad o ajustarse a los precedentes históricos relativos al dominio. A partir de estas motivaciones y compromisos de fondo, se intenta inferir una epistemología del dominio que respete estas restricciones. Por lo tanto, respetar las restricciones se convierte en una de las condiciones de éxito, si no la principal, para una explicación de la epistemología del dominio. Otorgar a estos criterios filosóficos una primacía metodológica y evidencial es lo que define el enfoque descendente. Sin embargo, un enfoque descendente no es nuestra única opción. En lugar de partir de supuestos establecidos sobre el área específica de conocimiento, podemos empezar con supuestos ejemplos de buenas prácticas epistémicas dentro del dominio relevante. A partir de estos ejemplos, podemos construir gradualmente una explicación de la epistemología del dominio, contrastando estas propuestas con casos cada vez más novedosos hasta encontrar una propuesta coherente con los casos disponibles. En otras palabras, un enfoque ascendente. Dado que este enfoque estudia la epistemología de un dominio mediante el análisis de las actividades de sus practicantes, también se conoce comúnmente como enfoque basado en la práctica. Si bien este enfoque está consolidado en las filosofías de la ciencia y las matemáticas, no ocurre lo mismo con la filosofía de la lógica. Como veremos, en la epistemología de la lógica sigue siendo común encontrar argumentos a favor de las propuestas basados ​​en su capacidad para evitar consecuencias escépticas, respetando al mismo tiempo las presunciones filosóficas preferidas por los autores. Sin embargo, este enfoque en el cumplimiento de criterios filosóficos predeterminados da como resultado explicaciones de la epistemología de la lógica que tienden a simplificar excesivamente los procesos implicados en la justificación de la lógica, a la vez que problematizan las prácticas reales de los lógicos. En consecuencia, el uso de un enfoque descendente es otra causa común de nuestra falta de progreso en la comprensión de la epistemología de la lógica. El objetivo de esta sección es destacar los beneficios de un enfoque basado en la práctica para la epistemología de la lógica. Si deseamos una explicación detallada de la epistemología de la lógica, lo mejor es analizar lo que realmente hacen los lógicos. Nuestra justificación para esta afirmación adopta dos formas. Primero, mostramos las ventajas que este enfoque ha proporcionado a nuestra comprensión de la epistemología de las ciencias y las matemáticas. Por analogía, dado que la lógica artificialis es un área de investigación al igual que las ciencias, sería sorprendente que este enfoque no ofreciera beneficios similares a nuestra comprensión de la epistemología de la lógica. Luego, argumentamos más directamente a favor del enfoque en lo que respecta a la epistemología de la lógica, mostrando que los enfoques descendentes han tenido consecuencias negativas en la filosofía de Lógica, centrándose en la defensa de Quine del holismo evidencial. Estos argumentos se utilizan como punto de partida para nuestra defensa más general de un enfoque basado en la práctica en las secciones siguientes, donde utilizamos este enfoque para ofrecer una epistemología informativa de la lógica artificialis. En este sentido, como ocurre con la mayoría de los métodos, la prueba del pudín estará al alcance de la mano. Dado que nuestra motivación inicial para un enfoque basado en la práctica de la epistemología de la lógica proviene de sus éxitos previos en las filosofías de la ciencia y las matemáticas, tiene sentido comenzar por ahí.

4.8.1 Motivación para el enfoque basado en la práctica 

El enfoque basado en la práctica se define, en primer lugar, por su insatisfacción con los enfoques de arriba hacia abajo y, en segundo lugar, su propuesta de cómo rectificar estas deficiencias. Surgió por primera vez en la década de 1960 en respuesta a las deficiencias percibidas en los enfoques filosóficos tradicionales hacia las ciencias^[17], que fueron criticados por producir explicaciones que eran: 

(i) demasiado idealizadas, al estar basadas en reflexiones a priori de cómo queremos que se vean las ciencias, o cómo deberían verse dadas nuestras preconcepciones, en lugar de reflejar la realidad de la investigación científica; 

(ii) demasiado simplistas, al no reflejar la pluralidad de objetivos y métodos dentro de la ciencia; (iii) demasiado centradas en el presente, cayendo en la trampa de una tendencia a producir historias antiguas  al presumir que la historia de la ciencia es una historia de progreso suave e imparable hasta el estado actual de las cosas; y 

(iv) demasiado centrado en el producto final, centrándose en las propiedades de las teorías y descuidando los procesos que llevaron al descubrimiento de estos resultados. 

Un ejemplo temprano de estas preocupaciones se encuentra en las críticas de Kuhn al falsacionismo de Popper, denunciado tanto por idealizar la metodología científica al presentar una imagen ingenua del progreso científico como una cadena continua de teorías cada vez más informativas que perpetuamente se refutan, como por estar demasiado centrado en el presente al presumir que los objetivos y las normas para la evaluación de las teorías científicas pasadas eran los mismos que los de la ciencia contemporánea. Además, Kuhn criticó las explicaciones anteriores de la metodología científica por prestar muy poca atención a la rica variedad de actividades que constituyen el método científico real, como el diseño y la prueba de equipos experimentales y su uso para medir constantes, en lugar de simplemente probar hipótesis. A principios del siglo XXI, comenzó una investigación práctica similar en la filosofía de las matemáticas, con enfoques tradicionales criticado por poseer una imagen demasiado idealizada de las matemáticas^[18]. La más prominente de estas preocupaciones fue la afirmación de larga data de que el conocimiento matemático está compuesto completamente de teoremas evidenciados por demostraciones formales. Contrario a esta visión, se argumentó que si uno mira la práctica matemática, la comprensión progresa de muchas maneras, incluyendo a través de demostraciones informales cuyas cualidades epistémicas positivas son irreducibles a las de las demostraciones formales^[19]. Además, similar a cómo los enfoques de arriba hacia abajo fueron criticados por pasar por alto elementos significativos del método científico, los filósofos de las matemáticas basados ​​en la práctica criticaron la filosofía tradicional de las matemáticas por descuidar características importantes de la empresa, incluyendo la evaluación de definiciones^[20] y el uso de diagramas^[21]. Por lo tanto, podemos ver dos motivaciones distintas para el enfoque. En primer lugar, su capacidad para proporcionar explicaciones más precisas sobre cómo se desarrolla la epistemología en el área de investigación, garantizando que nuestras propuestas filosóficas no conduzcan a que ciertas actividades en el campo se consideren epistémicamente inapropiadas. Esto, por supuesto, es lo que finalmente ocurrió con el falsacionismo de Popper, que negó a las afirmaciones probabilísticas y existenciales la condición de propiamente científicas. En segundo lugar, el enfoque puede proporcionar una comprensión más completa de la epistemología del campo al sacar a la luz características de su metodología que los enfoques descendentes pasan por alto. Después de todo, no podemos esperar que una teoría que parte de los primeros principios aprecie todos los procedimientos importantes que constituyen la metodología de un campo de investigación, como tampoco podemos esperar comprender los métodos de un maestro carpintero o un juez de un tribunal superior a partir de los primeros principios. Debemos observar lo que hacen. Es aquí donde el enfoque ha tenido éxitos significativos, a menudo poco reconocidos. Por ejemplo, el reconocimiento del papel de la construcción de modelos en las ciencias es un ejemplo paradigmático de cómo nuestra comprensión de la metodología científica ha mejorado significativamente al observar las prácticas de los científicos. Ahora no solo comprendemos bien los diversos propósitos y tipos de modelos científicos, sino que también contamos con descripciones detalladas de las diversas virtudes que los subcampos de la ciencia valoran en sus modelos^[22]. Nada de esto habría sido posible sin analizar en detalle las actividades de los científicos. Ambos beneficios de este enfoque son resultado de los intentos de rectificar las fallas percibidas de los enfoques tradicionales de arriba hacia abajo. En primer lugar, reorientando nuestros objetivos al ofrecer una explicación filosófica de la epistemología de un campo. En lugar de intentar construir grandes teorías unificadas sobre la naturaleza esencial de las ciencias o las matemáticas que se ajusten a nuestras preconcepciones sobre sus propósitos, objeto de estudio o epistemología, deberíamos aspirar a producir una comprensión de estos esfuerzos humanos que: 

(i) refleje la realidad de la investigación dentro de ellos; 

(ii) reconoce la pluralidad de objetivos y métodos que los atraviesan; 

(iii) sitúa los resultados en su contexto histórico adecuado; 

(iv) reconoce el desarrollo de las normas metodológicas del campo; y 

(v) presta la misma atención a los procesos de descubrimiento que a las propiedades de los productos finales. 

En segundo lugar, seleccionando los métodos apropiados para alcanzar estos objetivos. Específicamente, cuatro normas metodológicas son importantes para diferenciar el enfoque basado en la práctica de sus hermanos descendentes. Primero, la guía más confiable que tenemos para la epistemología de un campo son las actividades de sus profesionales. Por lo tanto, se debería dedicar más tiempo a observar cómo los científicos y matemáticos logran sus objetivos de investigación que a reflexionar sobre la naturaleza de la ciencia o qué constituye un objeto matemático. Esto no significa que la investigación no pueda estar motivada por presunciones o enigmas filosóficos. Pero, para ser probadas de manera confiable, las propuestas deben, en última instancia, enfrentarse al tribunal de la práctica real en el área de investigación. De forma análoga, si bien es perfectamente aceptable que las hipótesis científicas estén motivadas por diversas consideraciones, estas deben, en última instancia, resistir una rigurosa comprobación empírica. Es comprensible que gran parte de este trabajo se plasme en estudios de caso, ya sean estudios a fondo de las actividades de investigadores o equipos de investigación concretos, o estudios más amplios de las normas dentro de subcampos específicos. Sin embargo, también puede adoptar la forma de estudios historiográficos que examinen el desarrollo de técnicas o conceptos dentro de un campo. En segundo lugar, cuando existe un conflicto entre las prácticas destacadas en el campo y los supuestos filosóficos de fondo, se da prioridad a las prácticas dentro del campo. Esto se debe a que la forma en que los expertos justifican sus teorías es una guía más fiable de los objetivos, métodos y epistemología del área de investigación que nuestras presuposiciones filosóficas; por lo tanto, a las primeras se les debe dar (en la mayoría de los casos) mayor credibilidad. 

En tercer lugar, debemos ser cautelosos al hacer generalizaciones sin excepciones que vayan más allá de subcampos, programas de investigación o períodos de tiempo concretos, a menos que estén justificadas por los datos. Este es un corolario del uso de estudios de caso de la práctica real como datos primarios. Como con cualquier investigación empírica, se debe ser reticente, primero, a extrapolar demasiado más allá de la muestra hasta que se hayan encontrado resultados similares en otros lugares y, segundo, a presumir que los mismos hallazgos se mantendrán al modificar variables importantes, como el período de tiempo y el subcampo. Por supuesto, puede resultar que lo que descubramos para un período de tiempo o investigación Este programa es válido para otros, pero esta conclusión debe fundamentarse también analizando estos casos. Es importante destacar que nada impide que el filósofo que utiliza un enfoque basado en la práctica proponga generalizaciones audaces sobre la epistemología de un campo. De hecho, para que nuestras propuestas tengan algún poder predictivo, deben ir más allá de los casos considerados hasta ahora. Sin embargo, estas generalizaciones deben considerarse provisionales y requerir una mayor comprobación con nuevos casos adecuados. 

Finalmente, debemos estar abiertos a explorar características de los métodos del campo más allá de las que tradicionalmente los filósofos consideran serias. Esto no significa que todas las actividades que los profesionales realizan en su investigación sean de interés filosófico, pero no debemos limitarnos solo a las cuestiones filosóficas tradicionales (por interesantes que sean). Es esta característica del enfoque la que le ha permitido motivar preguntas de investigación novedosas y fructíferas sobre las ciencias que antes se descuidaban, incluyendo estudios sobre la construcción de modelos, el uso de pruebas asistidas por computadora^[23] y la relación entre las simulaciones y la experimentación^[24]. ¿Qué nos dicen, sin embargo, estos éxitos previos del enfoque sobre sus perspectivas dentro de la filosofía de la lógica, y en particular de la epistemología de la lógica? En primer lugar, nos proporcionan evidencia prima facie de que los mismos beneficios se aplicarán a la filosofía de la lógica, especialmente en lo que respecta a la epistemología de la lógica artificialis. Al fin y al cabo, la lógica artificialis es un campo de investigación con sus propios objetivos y métodos, como las ciencias. Además, sus actividades son realizadas por profesionales experimentados con experiencia demostrable. Esto ya respalda la conclusión de que el enfoque será un método más fiable para fundamentar nuestra epistemología de la lógica que los enfoques descendentes. Sin embargo, también podemos ser más directos en nuestro apoyo al enfoque. En primer lugar, destacando ejemplos en los que los enfoques descendentes han conducido a problemas similares en la epistemología de la lógica y en las filosofías de la ciencia y las matemáticas, y en segundo lugar, demostrando cómo el enfoque basado en la práctica puede ayudar a evitar estos problemas. Como era de esperar, este último objetivo se logra mejor mostrando lo que el enfoque puede lograr. Comenzamos con el caso para plantear preocupaciones similares contra los enfoques de arriba hacia abajo dentro de la filosofía de la lógica. 

4.8.2 Enfoques de arriba hacia abajo en la filosofía de la lógica

Los enfoques descendentes son comunes en la filosofía de la lógica. Kneale rechaza la posibilidad de lógicas específicas de dominio, ya que entonces la «lógica» se convertiría simplemente en «un nombre para cualquier conjunto de reglas según las cuales podemos argumentar en algún contexto». Las leyes lógicas son, por definición, completamente generales. Beall y Restall^[25], por otro lado, requieren que cualquier lógica genuina tenga una relación de consecuencia transitiva y reflexiva, a pesar de que existen programas de investigación bien desarrollados que proponen lógicas que rechazan la transitividad^[26] y la reflexividad^[27]. En cada caso, se consideran inviables prácticas o productos lógicos particulares por contravenir las expectativas filosóficas sobre la lógica, independientemente de si estas prácticas se toman en serio en el campo o no. Sin embargo, no es simplemente que se utilicen enfoques descendentes en la filosofía de la lógica. Hay buenas razones para pensar que las preocupaciones planteadas contra los enfoques descendentes en la filosofía de la ciencia también son pertinentes en la filosofía de la lógica, impactando nuestra comprensión de los objetivos, la epistemología y la metodología más amplia de la lógica. Tomemos, por ejemplo, la tendencia de los enfoques descendentes a llegar a generalizaciones apresuradas, lo que resulta en una imagen sincrónicamente homogénea injustificada del campo. 

Como vimos existe una presunción prominente en la literatura de que existe algún propósito canónico para la lógica, entendida como el "análisis del razonamiento^[28]" o la "codificación de la consecuencia lógica en el lenguaje natural^[29]". Sin embargo, no está claro qué justifica esta presunción para la lógica contemporánea. Históricamente, la logica artificialis estaba, de hecho, íntimamente conectada con la logica naturalis. Sin embargo, esto en sí mismo no es suficiente para determinar el propósito principal de la lógica formal ahora, ni de hecho que exista tal propósito. A falta de una simple presunción filosófica, la única justificación que encontramos son las apelaciones a la historia de la lógica. Cook, por ejemplo, intenta justificar su afirmación basándose en las opiniones de figuras fundadoras, como Aristóteles y Tarski^[30]. Sin embargo, Aristóteles también sugirió que la ciencia debería aspirar a proporcionar explicaciones teleológicas, y pocos científicos se toman en serio esta actividad en la actualidad. En general, apelar a las opiniones de las figuras fundadoras de un área de investigación para establecer su esencia es incurrir en la falacia embrionaria —la presunción de que una actividad tiene los mismos objetivos y propósitos que cuando se desarrolló inicialmente— y, de igual manera, nos obligaría a admitir que el propósito principal de la astronomía es proporcionar datos planetarios para el arte superior de la astrología. Así como las teorías y técnicas de un campo cambian con el tiempo, también pueden cambiar sus objetivos. El desarrollo de la lógica simbólica, y posteriormente de la teoría de modelos y demostraciones, abrió nuevas vías de investigación y usos de la lógica que ni Aristóteles ni (ni siquiera) Tarski pudieron prever. Centrarse en los usos de la lógica que primaron en su historia es ignorar los cambios ocurridos en las prioridades de investigación y el progreso teórico. Es como sugerir que el objetivo principal de la física moderna es explicar el comportamiento de los cuerpos en términos mecanicistas, porque así es como Newton y Descartes concibieron esta tarea. Un resultado desafortunado de especificar un propósito particular de la lógica como filosóficamente primario, basándose en precedentes, es que otros objetivos y usos de la lógica tienden a descartarse por ser indignos de estudio filosófico. Eklund, por ejemplo, afirma que cualquier forma de pluralismo lógico que no se centre en el propósito canónico o (filosóficamente) primario de la lógica carecería de interés^[31]. La implicación es que no es particularmente interesante filosóficamente que hayamos sido capaces de construir diversos sistemas lógicos diferencialmente adecuados para modelar una gama de fenómenos o alcanzar objetivos variables. Sin embargo, esto no solo minimiza las importantes innovaciones tecnológicas necesarias para producir estos resultados, sino que también es profundamente anacrónico. No había nada inevitable en el desarrollo de la lógica lineal ni en su fructífera aplicación para comprender la gramaticalidad de los idiomas.

También puede llevarnos a perder oportunidades de abordar cuestiones importantes sobre la lógica, como las supuestas similitudes entre su metodología y la de las ciencias. Los modelos científicos suelen transferirse con éxito de una ciencia a otra para modelar diversos fenómenos^[32]; los modelos epidemiológicos, por ejemplo, son aplicables no solo a enfermedades infecciosas, sino también a otros comportamientos infecciosos, como la desobediencia civil. Sin embargo, lo mismo ocurre con las estructuras matemáticas producidas por la lógica. Los sistemas formales, que inicialmente se propusieron para resolver un problema, se han aplicado posteriormente con éxito a otros. Los marcos de Kripke se utilizan ahora no solo para proporcionar semántica a las lógicas modales aléticas, sino también para modelar implicaciones deónticas y fenómenos doxásticos. La teoría de tipos pasó de ser un medio para evitar resultados paradójicos desagradables a utilizarse para modelar el razonamiento jurídico^[33]. Łukasiewicz introdujo la lógica multivaluada para comprender las modalidades. Sin embargo, ahora se utilizan lógicas trivaluadas para modelar los estados de los sistemas friccionales y resolver la paradoja de Painlevé en la dinámica de cuerpos rígidos^[34]. Si bien ahora podemos dar por sentadas estas aplicaciones de la lógica, no era en absoluto inevitable que la lógica evolucionara hasta convertirse en una disciplina con una variedad tan rica de sistemas y aplicaciones tan extensas. Centrarnos en un propósito particular de la lógica como el único "filosóficamente" interesante nos conducirá inevitablemente a una comprensión más pobre de la lógica, pasando por alto muchos de los avances tecnológicos y el consiguiente progreso "científico" que ha alcanzado. Logros que, en gran medida, se demuestran por la aplicabilidad cada vez mayor de estos sistemas y la capacidad de los lógicos para diseñar sistemas con el propósito de cumplir objetivos teóricos específicos. Es evidente, entonces, que un enfoque descendente puede llevar a una comprensión de la lógica como área de conocimiento más pobre de lo necesario. En comparación, un enfoque basado en la práctica, que presta mayor atención a las actividades de los investigadores en el campo, puede permitirnos apreciar estos logros y comprender las normas metodológicas del campo, incluyendo su similitud con las de las ciencias reconocidas. Particularmente relevante para nosotros es otra debilidad de los enfoques descendentes, común entre las propuestas de la epistemología de la lógica: la producción de explicaciones sobreidealizadas sobre cómo llegamos a estar justificados al creer en leyes o teorías lógicas, con la consecuencia de distorsionar nuestra comprensión de cómo se justifica la lógica. En la siguiente sección, mostramos cómo las explicaciones fundacionalistas de la lógica, que proponen que tenemos acceso inmediato a las leyes de la lógica, distorsionan los medios a través de los cuales se justifica la lógica. Aquí, sin embargo, nos centramos en una epistemología no fundacionalista de la lógica, que también está motivada por consideraciones descendentes y que incurre en los mismos problemas: el holismo evidencial de Quine.

4.9 El holismo evidencial de Quine 

A diferencia de las epistemologías fundacionalistas de la lógica, las epistemologías no fundacionalistas proponen que las leyes correctas de la lógica deben inferirse y justificarse con base en otras evidencias o compromisos que poseemos. Una de las epistemologías no fundacionalistas de la lógica más prominentes históricamente es el holismo evidencial de Quine, que afirma que nuestros compromisos lógicos se justifican como parte de nuestra red más amplia de creencias y se evalúan a la luz de la misma evidencia que las teorías dentro de las ciencias naturales. La propuesta de Quine tiene tres motivaciones principales. Primero, una profunda insatisfacción con las epistemologías fundacionalistas de la lógica existentes. Antes de la propuesta de Quine, había una suposición general de que uno obtenía acceso directo a las verdades de la lógica ya sea a través de la intuición o la analiticidad epistémica. Debido a sus propias propensiones naturalistas, Quine no tomó en serio la viabilidad de una facultad mental cuasiperceptual como la intuición; deberíamos confiar solo en aquellas fuentes epistémicas para las que tenemos respaldo científico. Sin embargo, a diferencia de otros empiristas, Quine también se mostró notoriamente impasible ante la sugerencia de que podríamos explicar nuestra justificación de las leyes lógicas en términos de analiticidad, dado que no existe una distinción de principios entre las oraciones en las que podemos justificarnos en creer solo mediante la competencia semántica (oraciones analíticas) y aquellas en las que no (oraciones sintácticas). Cualquiera que sea la forma de nuestra epistemología de la lógica, entonces, no puede depender ni de la intuición ni de la analiticidad. Esto nos lleva al argumento positivo de Quine para su propio holismo evidencial, que comprende dos factores. Primero, su compromiso con la tesis de Duhem-Quine: que una hipótesis individual no puede ser refutada (o verificada) concluyentemente de forma aislada. Dado que se requieren hipótesis auxiliares para deducir las consecuencias comprobables de una hipótesis objetivo, ante datos recalcitrantes, siempre podemos optar por atribuir la culpa a las hipótesis auxiliares en lugar de a la propia hipótesis objetivo. Por lo tanto, no está claro qué hipótesis debería rechazarse en tales situaciones. Con base en esto, Quine concluye que son las teorías completas (incluida nuestra lógica aceptada), y no las hipótesis individuales, las que se (des)confirman mediante la evidencia. Una vez que aceptamos que no tenemos acceso inmediato a las leyes lógicas correctas, dado que dichas leyes no pueden comprobarse de forma aislada, deben justificarse como parte de nuestra «red de creencias» general. Una consecuencia de la tesis de Duhem-Quine es que siempre es posible rescatar una creencia o proposición particular dentro de la red o teoría general ante datos recalcitrantes, realizando las modificaciones adecuadas en otras partes del sistema^[35]. Las leyes de la lógica no son diferentes. Una vez que se admiten estas leyes en la red comprobable, no hay ninguna razón de principio que impida su revisión ante datos problemáticos. Es cierto que las revisiones de las leyes lógicas deberían ser el último recurso, dada su centralidad en nuestra red de creencias y, por lo tanto, las amplias repercusiones que dicha revisión podría tener en nuestros compromisos generales. Sin embargo, todavía no hay garantía de que rechazar el silogismo disyuntivo o la ley del tercio excluido, por ejemplo, no sea nuestra mejor opción ante una contraevidencia extensa y drástica: la lógica, en principio, no está menos abierta a la revisión que la mecánica cuántica o la teoría de la relatividad... Si rara vez se proponen revisiones que corten tan profundamente como para tocar la lógica, hay una razón bastante clara para ello: el principio de mínima mutilación. La máxima basta para explicar el aire de necesidad que se asocia a la verdad lógica y matemática.

Esta máxima, que es la virtud teórica de realizar los cambios mínimos necesarios en nuestro sistema de creencias actual para adaptarnos a los datos recalcitrantes, sin perder simultáneamente los beneficios existentes del sistema, nos lleva a la segunda motivación positiva de Quine para su holismo evidencial: su compromiso con el empirismo, íntimamente ligado a su naturalismo: “Es un hallazgo de la propia ciencia natural, por falible que sea, que nuestra información sobre el mundo solo proviene de los impactos en nuestros receptores sensoriales”. Por lo tanto, para justificar cualquier afirmación, ya sea sobre el mundo físico, las matemáticas o la lógica, debemos recurrir exclusivamente a las fuentes de evidencia que se consideran naturalísticamente aceptables. No existe una división sustancial entre la evidencia que motiva nuestra elección de la lógica y la que justifica las teorías científicas. Las revisiones de nuestra teoría lógica, entonces, no se basan en argumentos de verdad analítica o fuentes a priori, sino en las mismas consideraciones que motivan otras revisiones dentro de nuestra red de creencias. Cualquier justificación (o revisión) de nuestra lógica se realiza como parte de la evaluación de nuestra red general de creencias, con la evidencia pertinente que no difiere en tipo de la utilizada para evaluar las teorías científicas. Es importante destacar que la propuesta de Quine se justifica no a través de una consideración detallada de cómo los lógicos sustentan sus teorías, sino más bien a través de tres factores filosóficos. Primero, una insatisfacción con las epistemologías fundacionalistas existentes de la lógica. Asumiendo que el escepticismo con respecto a la lógica es insatisfactorio, el fracaso de estas propuestas fundacionalistas implica la necesidad de una nueva epistemología no fundacionalista de la lógica: el holismo evidencial, respaldado por un compromiso con (i) la tesis de Duhem-Quine y (ii) el naturalismo. 

La justificación de Quine para su epistemología de la lógica es, por lo tanto, completamente descendente. Desafortunadamente, la propuesta resultante está en desacuerdo con la investigación lógica en varios aspectos, cada uno de los cuales problematiza la forma en que los lógicos realmente justifican las lógicas. En primer lugar, el holismo de Quine nos exige considerar todos los datos científicamente respetables como una posible motivación para revisar nuestra lógica. En principio, al menos, todas estas fuentes de datos reciben el mismo trato en cuanto a su posible importancia para la lógica. No debería haber distinción entre datos pertinentes a la lógica y datos pertinentes a otros campos. Sin embargo, esto minimiza la importancia que ciertos tipos de evidencia desempeñan dentro de la lógica. Por ejemplo, las paradojas lógico-semánticas no son simplemente una forma de datos recalcitrantes que deban tratarse junto con los resultados de las ciencias naturales. Ningún programa de investigación destacado en lógica se (re)evalúa sobre la base de su capacidad para dar sentido a los hallazgos de las ciencias biológicas. En cambio, la mayoría de los argumentos contemporáneos a favor de las lógicas no clásicas se basan en su capacidad para resolver problemas abiertos resaltados por las paradojas lógico-semánticas, algo que la lógica clásica (supuestamente) no puede. Las lógicas paracompletas se justifican con base en las paradojas semánticas respecto a la verdad^[36], las lógicas paraconsistentes con base en las paradojas de la teoría de conjuntos^[37]  y la lógica supervaluacionista con base en el sorites. Por lo tanto, si bien es cierto, como veremos en las siguientes secciones, que ciertos compromisos teóricos de las matemáticas y la lingüística se consideran relevantes para la empresa lógica, nuestras mejores teorías de la astrofísica y la microbiología no lo son. Sin embargo, en virtud de que los lógicos no permiten activamente que los hallazgos de estos campos informen nuestra lógica, el holismo evidencial de Quine considera la práctica actual de los lógicos totalmente inapropiada. 

En segundo lugar, debido a la máxima de mínima mutilación, el holismo de Quine propone que solo deberíamos esperar que se consideren revisiones de la lógica en las situaciones más drásticas, cuando todos los demás intentos de "salvar los datos" han fracasado. Esto se debe a que nuestros compromisos lógicos ocupan una posición privilegiada en el centro de la red de creencias, y por lo tanto, cualquier alteración de estos compromisos puede tener repercusiones de gran alcance. Sin embargo, como lo demuestran las lógicas no clásicas concebidas ante las paradojas lógico-semánticas, revisar la propia lógica no se considera simplemente la última opción drástica cuando todas las demás vías están cerradas. Más bien, es una opción viable incluso cuando existen otras vías. Lo sabemos porque existen soluciones clásicas para cada paradoja, que nos permiten adaptar los datos recalcitrantes realizando modificaciones en otras partes de la red. Por lo tanto, si bien siempre es posible salvar los datos sin revisar la propia lógica, estas no son las únicas opciones razonables que consideran los lógicos contemporáneos. En lo que respecta al holismo de Quine, los lógicos no clásicos contemporáneos cometen un error metodológico al intentar reemplazar la lógica establecida con éxito cuando existen otras revisiones. Sin embargo, una cosa es afirmar que los lógicos no clásicos están equivocados en sus argumentos revisionistas. mentos, y otro para afirmar que actúan de forma metodológicamente inapropiada. Rara vez los lógicos de mentalidad clásica responden a sus colegas no clásicos acusándolos de métodos inapropiados simplemente por promocionar soluciones no clásicas mientras que las clásicas sí lo son. Más bien, se reconoce que deben evaluarse los beneficios generales de las soluciones competidoras. De nuevo, el holismo de Quine problematiza innecesariamente una característica importante de cómo los lógicos justifican sus teorías.

4.10 Razones para el optimismo 

Aquí tenemos un caso claro en el que un enfoque descendente de la epistemología de la lógica ofrece una explicación sobreidealizada que problematiza cómo los lógicos justifican sus teorías. Afortunadamente, hay razones para el optimismo, ya que hemos visto cómo problemas similares planteados por enfoques descendentes dentro de las filosofías de la ciencia y las matemáticas se han resuelto al adoptar un enfoque orientado a la práctica. Hay buenas razones para pensar, entonces, que en principio se puede lograr lo mismo para la epistemología de la lógica. Al basar nuestra explicación de la epistemología de la lógica en los medios a través de los cuales los lógicos realmente justifican sus teorías, podemos esperar rectificar esas preocupaciones planteadas contra la propuesta de Quine. Sin embargo, una cosa es ser optimista y otra es cumplir estas promesas. Demostrar que el enfoque basado en la práctica puede cumplir es nuestro objetivo en la sección final. Pero antes de llegar allí, debemos considerar primero nuestra última deficiencia que debemos evitar: suponer que la epistemología de la lógica es inherentemente diferente de la de otras áreas, especialmente las ciencias reconocidas.

4.10.1 Fundacionalismo y la excepcionalidad de la lógica 

Hasta ahora, hemos argumentado que para comprender la epistemología de la lógica, necesitamos ir más allá de simplemente investigar las condiciones para un buen razonamiento (lógico) y considerar cómo justificamos nuestra aprobación de lógicas particulares. Además, que la mejor manera de obtener esta comprensión no se basa en el análisis conceptual o suposiciones establecidas sobre la naturaleza de la lógica, sino observando lo que los lógicos realmente hacen, utilizando un enfoque basado en la práctica. Esta sección aborda una tercera percepción común con respecto a la lógica que puede obstaculizar nuestra comprensión de su epistemología: la idea de que la lógica se distingue de las ciencias reconocidas en términos de su epistemología. La tradición sostiene que la lógica es excepcional^[38]. A diferencia de las leyes de otras áreas de investigación, las de la lógica se aplican por igual a todos los dominios. En esta medida, la lógica no se ocupa de la identidad particular de ningún objeto o propiedad. De hecho, la lógica no se ocupa del contenido de las proposiciones en absoluto, sino solo de su estructura formal. Por esta razón, las leyes lógicas no responden a las peculiaridades de los acontecimientos del mundo real como las de las ciencias. En consecuencia, si se conocen, sus leyes deben conocerse de una manera completamente diferente. Nos centramos aquí en las propiedades epistémicas que supuestamente hacen especial a la lógica y la diferencian de las ciencias; en particular, el carácter fundacional de la justificación lógica. Mientras que en las ciencias y las matemáticas solemos presuponer la validez de inferencias lógicas específicas para establecer conclusiones a partir de datos o axiomas dados, respectivamente, en la lógica parece que no podemos hacer esto sin plantear la cuestión. En consecuencia, la justificación de la lógica debe ser no inferencial y, por lo tanto, epistémicamente autosuficiente. En esta sección, tenemos dos objetivos. Primero, destacar las motivaciones para pensar que la epistemología de la lógica es distinta de la de las ciencias, en virtud de ser fundacional. En segundo lugar, demostrar que las dos visiones fundacionalistas más prominentes de la epistemología de la lógica, el racionalismo lógico y el semanticismo, son inadecuadas porque son incoherentes con la forma en que los lógicos justifican su lógica. Esto motiva nuestro análisis de las epistemologías no fundacionalistas de la lógica en la siguiente sección, y nuestra consecuente afirmación de que los mecanismos de elección de teorías en lógica no difieren mucho de los de las ciencias.

4.10.2 El estatus fundacional de la lógica 

En general, decir que una creencia es epistémicamente fundacional simplemente significa, en primer lugar, que nuestra justificación para esa creencia es autosuficiente y, por lo tanto, no depende para su justificación de ninguna otra creencia, y en segundo lugar, que nuestra justificación para algunas otras creencias depende (al menos parcialmente) de que tengamos justificación para estas creencias fundacionales. Por lo tanto, decir que (algunas de) nuestras creencias con respecto a la lógica son epistémicamente fundacionales significa que nuestra justificación para estas creencias es autosuficiente y que sirven para justificar (parcialmente) otras creencias que poseemos. Históricamente, ha habido dos razones para verse tentado a respaldar el fundacionalismo sobre la lógica. En primer lugar, permite abordar las preocupaciones escépticas no solo sobre las leyes lógicas en sí mismas, sino también sobre otros supuestos elementos de conocimiento que dependen evidentemente de la lógica, como los de las matemáticas. Si cada una de nuestras creencias requiere justificación, entonces, para evitar una regresión infinita, algunas de estas creencias deben tener justificaciones autosostenidas, y las relacionadas con la lógica son las candidatas más adecuadas. Esta justificación del fundacionalismo lógico es más evidente en los logicistas, como Frege, quienes buscan fundamentar (o explicar) los hechos matemáticos en términos de hechos lógicos. Si bien se nos dice que muchas verdades aritméticas carecen de evidencia y, por lo tanto, requieren prueba, las leyes lógicas primitivas son en sí mismas evidentes y, por lo tanto, no requieren argumentos adicionales^[39]. Por lo tanto, estas leyes lógicas primitivas pueden (supuestamente) soportar el peso fundacional de las matemáticas. En segundo lugar, el fundacionalismo es una respuesta natural a las preocupaciones sobre el inevitable arranque que ocurre si usamos creencias no lógicas para justificar leyes lógicas. Cualquier epistemología de la lógica que proponga que estamos justificados al creer en una ley lógica L en virtud de apelar a otros compromisos C enfrentará problemas, dice el fundacionalista, pues siempre necesitaremos apelar a reglas lógicas para demostrar que C es (in)consistente con L. En otras palabras, cualquier proceso justificativo no fundacionalista para leyes lógicas requiere hacer inferencias deductivas. Sin embargo, por supuesto, cualquier regla lógica en la que se base para hacer tales inferencias necesitará o no ser sancionada por el conjunto de leyes lógicas en consideración. Si lo son, entonces el defensor de las leyes simplemente está incurriendo en una petición de principio al confiar en la regla para el respaldo probatorio de las leyes. Por el contrario, si las leyes no sancionan la validez de la deducción, entonces, asumiendo que no hay una justificación no lógica alternativa para la deducción, las leyes socavan su propia justificación; la deducción resulta no estar justificada después de todo. En cualquier caso, la justificación de al menos algunas leyes lógicas debe ser no inferencial. Esta preocupación por las epistemologías no fundacionalistas de la lógica, conocida como el problema de la centralidad o el problema de la lógica de fondo^[40], es la principal motivación de las epistemologías fundacionalistas contemporáneas de la lógica^[41]. Presenta similitudes con las preocupaciones tradicionales planteadas contra los argumentos circulares que motivan las respuestas fundacionalistas al infame desafío pirrónico. Pero, en este caso, los casos problemáticos no son explícitamente circulares a las premisas, sino a las reglas, en el sentido de que cualquier argumento no fundacionalista para una lógica presupone la validez de una regla de inferencia al razonar hasta la conclusión del argumento justificativo, en lugar de incluir explícitamente la ley lógica concluyente como premisa.18 Una vez que se admite que nuestra justificación para (un subconjunto de) las leyes lógicas es fundacionalista, es probable que se deduzcan dos propiedades adicionales de la lógica: en primer lugar, que existe alguna propiedad consciente identificable asociada a esta justificación fundacional. Dado que el fundacionalismo requiere que uno esté justificado en creer estas leyes lógicas sin ningún apoyo evidencial de creencias adicionales, para tener acceso consciente a la buena reputación epistémica de estas leyes, debe haber alguna propiedad identificable de los estados de creencia relevantes asociados con su estado autosostenible, como la autoevidencia. Por supuesto, esto no requiere que exista tal propiedad identificable asociada, ya que es una posibilidad que, si bien tenemos una justificación autosostenible para leyes lógicas particulares, nunca podamos reconocer cuándo, de hecho, la tenemos. Sin embargo, este sería un resultado insatisfactorio para cualquier fundacionalismo con respecto a la lógica, dada la necesidad de responder a la pregunta de por qué deberíamos respaldar un conjunto de leyes lógicas L1 en lugar de otro, L2. 

En segundo lugar, en virtud de que la justificación es no inferencial, estas leyes lógicas deben estar justificadas por fuentes a priori. Esto se debe a dos factores. En primer lugar, la posibilidad de inferir evidencia para estas leyes específicas a partir de evidencia empírica está excluida por su estado fundacional; la evidencia de estas leyes privilegiadas no es inferencial. En segundo lugar, si bien esto no excluye la posibilidad de si no existe evidencia perceptual no inferencial que respalde estas leyes fundamentales, no existen estados de cosas observables viables que demuestren directamente que las leyes lógicas sean verdaderas. No vemos perceptualmente que el modus tollens o la contraposición son válidos, por ejemplo. Por lo tanto, si nuestra justificación de las leyes lógicas es autosuficiente, también es a priori.

4.10.3 Epistemologías fundacionalistas de la lógica 

Dos propuestas han dominado la literatura fundacionalista: el racionalismo lógico y el semanticismo. Si bien ambas coinciden en que la justificación de (algunas) leyes lógicas debe ser no inferencial y a priori, difieren en la fuente de esta evidencia a priori. Para los racionalistas, uno se justifica en creer en las leyes lógicas a través de una facultad intelectual cuasiperceptual, comúnmente conocida como intuición o intuición mental, en la que uno ve de manera no perceptual que una ley es verdadera. Tales intuiciones ahora se entienden comúnmente como fenomenológicamente similares a los estados perceptuales y, por lo tanto, capaces de representar estados de cosas^[42], proporcionándonos evidencia de la verdad o falsedad de sus contenidos, incluidas las leyes lógicas: Cuando tienes una intuición de que A, te parece que A . . . [entendido como un] tipo genuino de episodio consciente. Por ejemplo, cuando se considera por primera vez una de las leyes de De Morgan, a menudo no parece ni verdadera ni falsa; sin embargo, tras un momento de reflexión, algo sucede: ahora simplemente parece verdadera. Por lo tanto, simplemente vemos de manera no perceptual que la ley relevante es verdadera. En este sentido, nuestra justificación de las leyes lógicas es similar a la de otras verdades (putativas) necesarias, como las verdades conceptuales. Por el contrario, los semánticos niegan la necesidad de postular una nueva facultad cognitiva para dar cabida a la justificación lógica. En cambio, la justificación de las leyes lógicas se entiende en términos de competencia lingüística; en virtud de comprender el significado de los términos constituyentes de una ley lógica, automáticamente estamos justificados para asentir a su verdad: si uno sabe cuál es la función de las palabras “o”, “o” y “no”, entonces puede ver que cualquier proposición de la forma ·”O p es verdadera o p no es verdadera” es válida^[43].  Es decir, las leyes lógicas son epistémicamente analíticas.

La adhesión a una u otra de estas visiones fundacionalistas ha tendido a depender de los propios compromisos filosóficos, incluyendo las propias visiones metafísicas sobre la lógica y la viabilidad de fuentes de evidencia no naturalistas. En otras palabras, se basa en consideraciones de arriba hacia abajo. Por ejemplo, los semanticistas, como los positivistas lógicos, se vieron motivados a aceptar la analiticidad de la lógica basándose en su escepticismo sobre la existencia de una facultad cognitiva especial que proporciona una comprensión directa de las verdades de la lógica y, además, en el deseo de aceptar la supuesta verdad necesaria de las leyes lógicas sin tener que recurrir a la dudosa noción de la necesidad metafísica^[44]. Al adoptar la analiticidad metafísica y epistemológica conjunta de las leyes lógicas, los semantistas esperaban explicar simultáneamente la aparente verdad necesaria de las leyes de la lógica en términos de convenciones lingüísticas, en lugar de las formas en que el mundo debe ser, a la vez que explicaban nuestra justificación para adoptar estas leyes en virtud de la comprensión adecuada de su contenido semántico (similar a otras verdades analíticas monótonas, como “Todas las zorras son zorras”). En comparación, los racionalistas desean defender la objetividad de la lógica, que, según creen, el semantista ha desechado al relegar la lógica al estatus de convenciones. Esto a menudo intentan lograrlo rechazando el naturalismo y admitiendo tanto hechos abstractos no espaciotemporales como una facultad especial, la intuición racional, para acceder a ellos^[45]. Por lo tanto, ni los racionalistas ni los semantistas se motivan generalmente por las formas de evidencia a las que los lógicos apelan para justificar su lógica. Más bien, partiendo del supuesto de que nuestra justificación de (algunas) leyes lógicas debe ser no inferencial y a priori, se presupone que una postura como el racionalismo o el semanticismo debe ser correcta si queremos evitar la desafortunada conclusión escéptica de que carecemos de conocimiento sobre lógica^[46]. Además, la respuesta a cuál de estas propuestas se debe favorecer no se basa en cuál nos proporciona una respuesta más realista a la justificación lógica, sino, en primer lugar, cuál es más adecuada para evitar conclusiones escépticas indeseadas y, en segundo lugar, cuál es compatible con otros compromisos que sus defensores adoptan, como el naturalismo o el realismo sobre los hechos lógicos. Dado nuestro argumento a favor del enfoque basado en la práctica en la sección anterior, la pregunta pertinente para nosotros aquí no es si alguna de estas propuestas cumple con sus objetivos de arriba hacia abajo. Ese es un método ineficaz para determinar la precisión de una epistemología de la lógica. Más bien, nos preocupa cuán plausibles son ambas propuestas, dado nuestro conocimiento sobre cómo se evalúan las lógicas. En particular, el grado en que las posiciones problematizan los debates reales que los lógicos mantienen sobre las leyes lógicas correctas y las formas de evidencia que utilizan. Cualesquiera que sean las otras virtudes que posea una epistemología de la logica artificialis, si no puede tener sentido de la amplia gama de formas en que los lógicos justifican sus teorías, este es un problema para la teoría epistemológica, no para los profesionales.

4.10.4 Desafíos a la visión fundacional 

Para evaluar adecuadamente estas epistemologías fundacionalistas a la luz de la práctica lógica, primero debemos comprender cómo esperaríamos que fuera la epistemología de la lógica si cualquiera de las propuestas fuera cierta. Según el racionalismo, obtenemos la justificación de las leyes lógicas (fundamentales) directamente de las intuiciones sobre la ley. Simplemente vemos que es cierta. Por lo tanto, si el racionalismo fuera cierto, esperaríamos que los argumentos sobre la lógica correcta estuvieran llenos de apelaciones a las intuiciones, especialmente cuando se trata de las leyes fundamentales en las que se basa el resto de la lógica. De manera similar, cuando hay desacuerdo sobre la verdad de afirmaciones importantes, deberíamos encontrar que las partes apelan directamente a sus intuiciones sobre la verdad de las afirmaciones relevantes. De hecho, para el racionalista, no hay nada más a lo que el lógico pueda apelar. Si la otra parte discrepa con nosotros, todo lo que podemos hacer es sugerir que nuestro interlocutor no tiene las intuiciones adecuadas y buscar con más atención. El semanticista se encuentra en una posición similar. Según ella, obtenemos justificación para nuestras leyes lógicas directamente al comprender su significado. Una vez que comprendemos sus partes constituyentes, estamos inmediatamente justificados para creer en su verdad. Por lo tanto, si existiera algún desacuerdo sobre la verdad de una ley, se esperaría que cada parte apelara al significado de la ley pertinente para fundamentar sus propias afirmaciones sobre su verdad o falsedad. Si nuestro interlocutor no asiente a las mismas leyes que nosotros, nos comprometemos a decir que esto se debe simplemente a que, de alguna manera, ha malinterpretado su contenido. Todo lo que podemos hacer en este caso, con la esperanza de rescatar la situación, es señalar el significado de la ley de forma aún más explícita. Ahora que comprendemos mejor cómo esperaríamos que fueran los debates lógicos si el racionalismo o el semanticismo fueran ciertos, unas cuantas advertencias. En primer lugar, quienes defienden ninguna de las dos posturas tienen claro el objeto exacto de estas creencias fundamentales: si son reglas de inferencia, esquemas argumentativos u otra cosa. Esto plantea una complicación a la hora de evaluarlas. Por ejemplo, si nos centráramos en cómo los lógicos justifican la validez de las reglas de inferencia o los esquemas argumentativos, siempre es posible que el fundacionalista responda que nuestras críticas no son acertadas, ya que nunca se preocuparon por la justificación de estos compromisos particulares, sino por algo más. Este es un problema inevitable a menos que el fundacionalista esté dispuesto a especificar la forma exacta que adoptan estas creencias fundacionales.

En segundo lugar, el fundacionalista no se compromete a que toda ley lógica (comoquiera que se conciba) sea fundacional y, por lo tanto, justificada no inferencialmente. Más bien, todo lo que se requiere es que un subconjunto privilegiado de las leyes esté justificado fundacionalmente, y que las demás leyes que componen la lógica estén justificadas derivativamente. Esto genera otra complicación, ya que, a menos que el fundacionalista especifique qué leyes sirven como fundamentos, nunca podemos estar seguros de tener evidencia en contra de su propuesta; siempre pueden justificar los casos problemáticos proponiendo que la ley específica en consideración no es fundacional y, por lo tanto, el hecho de que los lógicos no la traten como tal no plantea ningún problema para su explicación. Afortunadamente, ambas complicaciones tienen una solución razonable. Si bien una lógica implica más que el esquema argumental o las reglas de inferencia que valida, una parte importante de lo que constituye desacuerdos entre las lógicas y los lógicos que las defienden es la divergencia sobre los respectivos conjuntos de esquemas o reglas de inferencia válidos. Además, si el fundacionalismo fuera cierto, incluso si la supuesta (in)validez de estos esquemas argumentativos o reglas de inferencia no constituyera las creencias lógicas fundacionales para las que tenemos justificación no inferencial, esperaríamos que los desacuerdos sobre el esquema argumentativo o las reglas eventualmente se "fundamentaran" en un desacuerdo sobre uno de los compromisos lógicos fundacionales. Después de todo, este es precisamente el punto del fundacionalismo: las creencias fundacionales respaldan las no fundacionales. Por lo tanto, si hay desacuerdo sobre si una regla de inferencia o esquema argumentativo no fundacional es (in)válido, ese desacuerdo debe ser causado en última instancia por un desacuerdo sobre las creencias fundacionales que lo justifican o por el razonamiento de las creencias fundacionales a las no fundacionales. Por lo tanto, podemos proceder con seguridad y considerar las formas en que los lógicos justifican sus lógicas, que contienen conjuntos de esquemas argumentativos válidos y reglas de inferencia, sabiendo que si estas lógicas se justificaran en última instancia sobre la base de compromisos lógicos fundacionales, esto se manifestaría en forma de apelaciones a intuiciones relativas a estos compromisos o definiciones cuando surgieran desacuerdos. Otra complicación, de difícil solución, es la posibilidad de que el fundacionalista rechace la asociación entre el carácter fundacional de una ley y su posesión de alguna propiedad identificable, como la autoevidencia. Hacerlo, en efecto, divorciaría los procesos justificatorios conscientes ejemplificados por la práctica de los lógicos al elegir una teoría de la realidad de por qué estamos realmente justificados al mantener ciertos compromisos lógicos. Esto garantizaría automáticamente que nada de lo encontrado en los debates lógicos reales pudiera contradecir la propuesta fundacionalista, ya que no deberíamos esperar que el fundacionalismo tenga consecuencias identificables en lo que respecta a las razones a las que los lógicos tienen acceso y utilizan para argumentar a favor de una lógica.

Ante esta respuesta, lo mejor que podemos hacer es seguir adelante, reconociendo que cuanto menor sea la relación del fundacionalismo con las razones a las que tenemos acceso, menos relevante será para quienes deseamos comprender por qué los humanos están justificados al respaldar una lógica en lugar de otra. Quizás las razones que esgrimen los lógicos para respaldar sus lógicas preferidas sean epifenoménicas, pero en ese caso, no está claro por qué no deberíamos decir lo mismo de los científicos y matemáticos. Siempre es posible plantear la hipótesis de un mecanismo justificativo y sugerir que, en realidad, contrariamente a lo que parece indicar la labor de los investigadores en este campo, es este otro mecanismo (no aparente) el que justifica las teorías pertinentes. Pero, en este caso, considero que la propuesta no es más evaluable que la existencia de una partícula indetectable. Procedamos, pues, asumiendo que, si el fundacionalismo fuera cierto, veríamos sus efectos en cómo los lógicos argumentan sus lógicas. Nos centramos aquí en dos preocupaciones que son especialmente problemáticas para el fundacionalismo sobre la lógica: primero, que los lógicos hacen pocas (o ninguna) apelaciones a la autoevidencia de una ley lógica, confiando en cambio en juicios sobre argumentos específicos para apoyar sus teorías; segundo, que las paradojas lógico-semánticas juegan un papel importante en la evaluación de las lógicas.

4.10.5 Apela a inferencias específicas, no a leyes lógicas

En primer lugar, si el fundacionalismo sobre la lógica fuera cierto, esperaríamos que los desacuerdos sobre la lógica correcta se manifestaran como apelaciones directas a leyes contrapuestas. Que, contrariamente a lo que sugieren los defensores de la lógica L2, alguna ley o compromiso L dentro de L1 es evidente. Si los defensores de L2 no pueden apreciar este hecho, es su propia deficiencia; o bien tienen intuiciones erróneas sobre L o no comprenden completamente su contenido. Sin embargo, rara vez, o nunca, los lógicos apelan directamente a la evidencia de leyes particulares o compromisos teóricos. En cambio, apelan a la aceptabilidad de argumentos o inferencias específicos. La (supuesta) aceptabilidad de esta inferencia específica se utiliza entonces como dato para criticar a las lógicas contrapuestas por su incapacidad para sancionar esta inferencia con las leyes que contienen. Consideremos algunos ejemplos breves de este fenómeno. Primero, tomemos el análisis de Williamson de las soluciones multivaluadas del sorites. En lugar de apelar directamente a la corrección de las reglas de inferencia clásicamente válidas que las lógicas no clásicas invalidan, para socavar estas últimas, Williamson produce ejemplos de inferencias específicas que consideramos aceptables pero que las lógicas no clásicas consideran inválidas. Por ejemplo, Williamson  critica la lógica gappy de tres valores de Halldén por considerar inválida la inferencia de "Jack no es un filósofo" a "Jack no es un filósofo calvo" cuando Jack es un caso límite de calvicie, aunque la inferencia es perfectamente correcta independientemente del estado relativo de calvicie de Jack. Por lo tanto, la lógica es criticada por su incapacidad para sancionar inferencias específicas que consideramos aceptables. Otro ejemplo proviene de la crítica de Burgess^[47] a las lógicas relevantes para invalidar el silogismo disyuntivo. Nuevamente, para fundamentar su preocupación, Burgess no se limita a apelar a la autoevidencia del silogismo disyuntivo. Más bien, señala que las demostraciones matemáticas informales hacen un uso destacado de inferencias (supuestamente) sancionadas por la regla. El argumento de Burgess difiere del de Williamson únicamente en que, en lugar de citar ejemplos específicos de demostraciones informales que (supuestamente) requieren el silogismo disyuntivo para fundamentar su validez, da por sentado que existen inferencias dentro de las demostraciones informales que ejemplifican el esquema del lenguaje natural: 

A o B 

no B

___

 A 

Además, en virtud de que tales inferencias ocurren regularmente dentro de la práctica epistémica confiable de las matemáticas, deben ser buenas inferencias. Tennant utiliza un argumento similar para criticar el dialeteísmo, la visión de que algunas contradicciones son verdaderas, cuyos defensores adoptan una lógica paraconsistente excesiva (como la PL^[48]). Tennant critica tales lógicas no sobre la base de que invaliden ciertas reglas de inferencia que son evidentemente verdaderas, sino sobre la base de que, hasta donde sabemos, necesitamos estas reglas para justificar movimientos inferenciales importantes dentro de las pruebas matemáticas. Si el dialeteísta cree que está equivocado, debería mostrarnos cómo estas pruebas informales pueden ser regimentadas dentro de su lógica. Por lo tanto, cuando se les desafía, los lógicos rara vez intentan establecer la verdad de una ley lógica basándose en su evidencia. Lo mismo puede decirse de quienes rechazan una ley. Esto se ve más claramente en el caso de los desafíos directos a las leyes clásicamente válidas establecidas con contraejemplos concretos, como el famoso contraejemplo putativo de McGee al modus ponens y el contraejemplo putativo de Yalcin al modus tollens con condicionales que contienen un operador de probabilidad. En ninguno de los casos se utilizan intuiciones sobre la ley misma para socavarla. Más bien, se buscan instancias que la refuten. Sin embargo, la evidencia más sólida que tenemos contra el fundacionalismo no es simplemente la ausencia de apelaciones a la autoevidencia, sino la evidencia que tenemos de que la elección de teoría en lógica funciona a través de un proceso inferencial y constructivo. Es todo menos directo. Si bien las leyes lógicas impactan nuestras conclusiones sobre la validez de los argumentos en lenguaje natural, dichas leyes no se expresan en un lenguaje natural. Las lógicas se formulan en un lenguaje artificial, conectadas a argumentos del lenguaje natural mediante reglas de traducción (o representación^[49]). Si el fundacionalismo fuera cierto, esperaríamos que los lógicos apelaran a la autoevidencia de estas leyes lógicas en el lenguaje artificial y luego argumentaran, sobre la base del establecimiento de estas leyes, que los argumentos particulares del lenguaje natural son válidos dadas algunas reglas de traducción adecuadas. En otras palabras, si bien tenemos una visión directa de la verdad de ciertas leyes lógicas, luego inferimos la validez de argumentos específicos. Sin embargo, lo opuesto es lo que encontramos en los debates lógicos. Es la aceptabilidad de inferencias específicas lo que se utiliza para fundamentar las afirmaciones sobre la corrección de las leyes, no al revés. Si algo se da por sentado (o es evidente por sí mismo) en los debates lógicos, es la aceptabilidad de argumentos o inferencias específicos, no las leyes en sí mismas. De hecho, no solo se apela a argumentos del lenguaje natural «obviamente» aceptables, sino que dichas apelaciones a menudo tienen fuerza probatoria porque existe un acuerdo general entre las partes involucradas sobre la (in)aceptabilidad de los argumentos pertinentes. En cambio, en lo que las partes tienden a discrepar es en cómo estos argumentos aceptables deberían formalizarse en leyes lógicas. El desacuerdo depende, entonces, no de la autoevidencia de una ley lógica específica, sino de cómo sancionar la validez de estos argumentos específicos dentro de una lógica. El debate relevantista sobre la validez del silogismo disyuntivo lo demuestra claramente. Aunque Anderson rechazan el silogismo disyuntivo, coinciden con el lógico clásico en que muchos argumentos de la forma esquemática del lenguaje natural (D) son válidos, particularmente en matemáticas^[50]. En otras palabras, ambas partes están de acuerdo en estos casos, pero discrepan sobre cómo deben formalizarse los argumentos para explicar su validez. Esto queda demostrado.

Por lógicos relevantes que asumen la tarea de demostrar cómo la validez de estos argumentos puede conciliarse con un nuevo sustituto relevante del silogismo disyuntivo, utilizando una disyunción intensional llamada fisión. Por lo tanto, el lógico clásico no se equivocó respecto a los argumentos del lenguaje natural; de hecho, son válidos. Simplemente los confundió con ejemplos del silogismo disyuntivo clásicamente válido. En realidad, son ejemplos de la propia versión del silogismo del lógico relevante utilizando una disyunción intensional. El punto central del desacuerdo se centra entonces en si alguna de estas leyes lógicas formaliza fielmente los argumentos pertinentes del lenguaje natural^[51]. Un punto similar se puede hacer con el rechazo del dialeteísta del modus ponens clásico usando el condicional material. Lo hacen no basándose en encontrar la ley evidentemente falsa, sino porque las paradojas autorreferenciales (supuestamente) nos dan razón para creer que algunas proposiciones son tanto verdaderas como falsas^[52]; en otras palabras, que existen excesos de valores de verdad. Si uno mantiene fija la semántica estándar para la disyunción y la negación, y entiende la consecuencia lógica como preservación de la verdad, admitir excesos de valores de verdad proporciona directamente un contramodelo a {A → B, A} ⊨ B; simplemente permita que A sea un exceso mientras que B es simplemente falso. Sin embargo, al rechazar el modus ponens clásico, el dialeteísta no afirma con ello que los usos de un condicional desprendible en las matemáticas y las ciencias sean generalmente inválidos. Están de acuerdo con el lógico clásico sobre la validez de vastas franjas de argumentos de la forma de lenguaje cuasi-natural “Si A entonces B, A, por lo tanto B” (y otras expresiones del condicional indicativo); simplemente discrepan sobre la ley lógica que explica la validez de estos argumentos de lenguaje natural. Nuevamente, esto se demuestra por el dialeteo asumiendo la carga teórica de encontrar un nuevo condicional capaz de sancionar estas inferencias aceptables dentro de las ciencias mientras que es compatible con su compromiso con la existencia de excedentes.26 Incluso cuando no hay acuerdo sobre la (in)aceptabilidad de la inferencia específica, todavía hay un reconocimiento de que, debido a que la supuesta (in)aceptabilidad de una inferencia es pertinente para evaluar una lógica, cualquier evidencia de este tipo no puede ser rechazada de plano sino que debe abordarse de alguna manera. Esto se muestra por las respuestas al contraejemplo de McGee al modus ponens.^[53] En lugar de simplemente rechazar el caso problemático apelando a la autoevidencia del modus ponens, encontramos intentos de: (i) explicar el supuesto contraejemplo mostrando que en realidad no es una instancia de la ley, o que confunde razones para creer racionalmente con la verdad, o (ii) acomodarlo proporcionando una nueva versión no afectada del modus ponens^[54]. Estos casos ejemplifican un proceso mediado en el que nuestros juicios sobre inferencias específicas informan nuestra teoría de la lógica, y hacemos todo lo posible para acomodar estos juicios como datos con nuestras leyes postuladas. Esto, por supuesto, requiere que se hagan inferencias de los argumentos específicos a las supuestas leyes lógicas. Todo lo cual es contrario a lo que propone el fundacionalismo. La imagen de la metodología de la lógica que obtenemos de estos casos no es una de comprensión directa de las leyes lógicas, sino un proceso constructivo donde se proponen leyes para sancionar argumentos e inferencias admitidos como aceptables. Además, las propuestas competidoras son criticadas sobre la base de no cumplir con éxito estos desiderata. Antes de pasar al desafío planteado por las paradojas lógico-semánticas, cabe destacar dos puntos más sobre las apelaciones a la autoevidencia dentro de la lógica. En primer lugar, si bien hemos enfatizado la rareza de las apelaciones a la evidencia de las leyes lógicas, no afirmamos que nunca ocurran. Siempre hay casos atípicos. Sin embargo, en los raros casos en que se apela a la evidencia de las leyes, estas rara vez tienen validez, lo que sugiere que la comunidad las considera evidencialmente vacías. Por ejemplo, uno de los pocos casos en que se hace tal apelación, el intento de Slater^[55] de refutar el dialeteísmo afirmando que, por definición, las contradicciones nunca podrían ser conjuntamente verdaderas, fracasó por completo. El debate sobre las virtudes (y vicios) del dialeteísmo continuó a pesar de todo. Esto demuestra que los lógicos generalmente no se conforman con justificar la lógica basándose en apelaciones a la evidencia de las leyes o definiciones. En segundo lugar, cuando se apela a las leyes lógicas, no suelen hacerse en el contexto de aportar nueva evidencia para una lógica. Más bien, son apelaciones post hoc, que resumen aspectos de nuestra teoría lógica actualmente aceptada, que ya ha sido respaldada independientemente. En otras palabras, sirven como recordatorios para no revisar ciegamente ese aspecto particular de la teoría, dado que cuenta con un respaldo independiente significativo. Las apelaciones, por lo tanto, carecen de peso probatorio. Un ejemplo de esto proviene nuevamente del análisis de Williamson  sobre la vaguedad, donde critica algunas semánticas no clásicas por no respetar la funcionalidad veritativa, lo que llevaría a la pérdida de muchas de las ventajas obtenidas por la lógica clásica. En este sentido, tales apelaciones a leyes establecidas no parecen exclusivas de la lógica; es común en las ciencias apelar a una ley o teoría bien establecida como reductio a alguna propuesta novedosa. Sin embargo, en este caso, no es la apelación a la ley o teoría en sí la que proporciona el respaldo probatorio, sino el hecho de que ya cuenta con un respaldo independiente sólido.

4.11 Metafísica 

Es hora de cambiar la forma en que pensamos sobre la metafísica. Tradicionalmente, la metafísica se presenta como un área de la filosofía cuyo objetivo es descubrir hechos altamente generales, básicos o fundamentales sobre el mundo. Esta concepción de la metafísica aparece en casi cualquier texto introductorio sobre el tema. Jonathan Lowe, por ejemplo, sostiene que la preocupación central de la metafísica es la estructura fundamental de la realidad en su conjunto^[56].

Peter van Inwagen está de acuerdo: cuando me introdujeron en la metafísica como estudiante, me ofrecieron la siguiente definición —la metafísica es el estudio de la realidad última—. Esta sigue siendo, según él, la mejor definición de metafísica que ha encontrado^[57].

Esta forma de pensar la metafísica se originó mucho antes de que las investigaciones filosóficas y las ciencias naturales se separaran; de hecho, mucho antes de que la ciencia natural, tal como la conocemos ahora, comenzara a desarrollarse y practicarse sistemáticamente. En ese contexto, tal vez era natural concebir la metafísica como una investigación básica sobre la estructura de la realidad, como parte de un amor por la sabiduría general.

Pero hoy, esta forma tradicional de entender la metafísica parece haberse vuelto obsoleta y, en muchos sentidos, innegablemente problemática. Porque si la metafísica realmente se concibe a sí misma como el descubrimiento de hechos sobre la realidad, queda atrapada en una rivalidad con las ciencias, una rivalidad que parece destinada a perder. Stephen Hawking expresó con claridad este escepticismo al escribir^[58]: “La gente siempre se ha hecho multitud de preguntas: ¿cómo podemos comprender el mundo en el que nos encontramos? ¿Cómo se comporta el universo? ¿Cuál es la naturaleza de la realidad? ¿De dónde vino todo esto? Tradicionalmente, estas han sido preguntas para la filosofía, pero la filosofía está muerta. La filosofía no se ha mantenido al día con los desarrollos modernos de la ciencia, particularmente la física. Los científicos se han convertido en los portadores de la antorcha del descubrimiento en nuestra búsqueda del conocimiento.”

Este es un desafío familiar para la filosofía, que ha existido desde que, en el siglo XVII, las ciencias naturales comenzaron a separarse de lo que alguna vez se llamó filosofía natural. A medida que la física, la química, la biología y otras ciencias se volvieron explícitas respecto de sus propios objetivos, métodos y criterios de éxito, persistió una pregunta: ¿qué queda entonces para la filosofía? Una respuesta común ante la amenaza de una rivalidad con las ciencias ha sido afirmar que el trabajo de la metafísica es más general que el de las disciplinas científicas. Como señala Robin LePoidevin, “una forma de distinguir la metafísica de la ciencia es señalar el nivel de generalidad en la discusión metafísica^[59]”. Es decir, la metafísica es general en el sentido de que se ocupa de todo tipo de temas: podemos indagar sobre la estructura metafísica del mundo físico, de los números, de las propiedades o de la libertad.

Podemos formular preguntas metafísicas sobre el mundo social, la raza, el género o las estructuras institucionales; también sobre la metafísica de los objetos geográficos, el arte o los artefactos. Incluso podemos interrogar la metafísica de lo modal, preguntándonos por la existencia de hechos modales o de mundos posibles; o adentrarnos en la metaética y examinar las propiedades, normas y reglas morales desde una perspectiva metafísica. Es esta afirmación de generalidad la que otorga a la metafísica gran parte de su interés, así como su aparente diferencia frente al trabajo de las ciencias naturales. Como sostiene Karen Bennett, al menos uno de los proyectos centrales de la metafísica puede entenderse como “investigar la naturaleza de ciertos fenómenos particularmente desconcertantes que parecen, de alguna manera, recalcitrantes a la investigación puramente empírica: la conciencia, la libertad, el tiempo, las leyes de la naturaleza y lo modal^[60]”.

Pero incluso si entendemos la tarea de la metafísica de esta manera general, esto todavía no la libera de una aparente rivalidad con las ciencias, allí donde las ciencias —ya sean físicas o sociales— tratan los mismos temas relevantes. Cuando surgen conflictos entre las afirmaciones de la metafísica y las de las ciencias, parece razonable conceder prioridad a las segundas. A medida que las ciencias naturales han ido convergiendo gradualmente en sus resultados y proporcionando la base para impresionantes logros tecnológicos y médicos, sus credenciales para hablarnos del mundo se han vuelto bastante sólidas. Por el contrario, las “teorías” de los filósofos, lejos de converger, han proliferado con el paso del tiempo, generando propuestas cada vez más radicales y contraintuitivas. Algunos ejemplos notables son la idea de que no existen objetos inanimados compuestos^[61], que no existen personas^[62], o que hay una multiplicidad de mundos posibles, aislados espacial y causalmente unos de otros^[63].

En resumen, en metafísica —a diferencia de las ciencias empíricas— no tenemos nada parecido a una convergencia hacia la verdad que asegure que estamos progresando en el descubrimiento de los “hechos” relevantes sobre el mundo. En cambio, nos avergüenza una proliferación cada vez mayor de puntos de vista. Si concebimos la filosofía como una disciplina cuyo objetivo es decirnos “cómo es el mundo”, entonces parece quedar atrapada en una rivalidad con las ciencias. Y esa es, sin duda, una rivalidad destinada a perder.

La proliferación de puntos de vista metafísicos también ha llevado a algunos, tanto dentro como fuera de la filosofía, a un escepticismo desesperado. Parece que nunca llegaremos a conocer las respuestas a las preguntas metafísicas y, si es así, tal vez sería mejor darnos por vencidos y dirigir nuestros esfuerzos hacia un terreno más útil. De hecho, la mera proliferación de posturas filosóficas y los repetidos fracasos en alcanzar la convergencia podrían, por sí solos, alimentar una profunda duda sobre el valor del pensamiento metafísico. Aquí hay una forma de intentar cuantificar este fenómeno: la primera gran encuesta filosófica se realizó en el año 2000.  Fue una encuesta realizada a 3,226 filósofos, la gran mayoría de ellos profesores de filosofía, quienes expresaron su opinión sobre 30 preguntas filosóficas centrales: cuestiones acerca del libre albedrío, la existencia de Dios, la objetividad del valor estético o qué cuenta como conocimiento. Generalmente, se ofrecían dos opciones de respuesta. Bryan Frances llevó a cabo un análisis estadístico de los resultados^[64]. Como resultado, Bryan Frances argumentó que la gran mayoría de quienes creen poseer conocimiento sobre estos temas controvertidos, en realidad, no lo tienen. El desconcierto radical en filosofía podría incluso conducirnos a un letargo escéptico, haciéndonos pensar que, por muy indescubribles que sean estos hechos, quizá sea mejor abandonar la búsqueda y dirigir nuestra atención hacia otro ámbito.

Se ha vuelto cada vez más común que los propios filósofos expresen dudas acerca de que las respuestas a las preguntas metafísicas puedan conocerse. Robert Nozick argumenta que debemos ser escépticos respecto a la posibilidad de tener algún conocimiento sobre lo que es metafísicamente necesario o posible^[65]. Karen Bennett defiende una posición epistémica, según la cual, en muchas disputas metafísicas sobre lo que existe, hay poca justificación para creer en cualquiera de los lados^[66]. Edouard Machery expresa un escepticismo similar respecto a numerosas preguntas filosóficas tradicionales, argumentando que muchas de ellas requieren una forma de conocimiento modal que no podemos poseer. Decir, en general, qué se requiere para el conocimiento, o para que un acto sea moralmente permisible, o para que un agente sea libre, implica saber qué sería el caso en todos los mundos posibles. Pero —argumenta— no podemos obtener ese tipo de conocimiento modal^[67]: “Si bien puede haber tales hechos —escribe—, no podemos conocer muchas de las posibilidades y necesidades metafísicas de interés filosófico; por lo tanto, estos problemas no pueden resolverse. Sugiero que haríamos mejor en suspender el juicio y abandonar la esperanza de resolver cuestiones filosóficas modalmente incómodas”. Tal escepticismo no parece fuera de lugar, dados los formidables misterios epistemológicos acerca de cómo podríamos llegar a conocer los hechos que la metafísica supuestamente pretende descubrir. 

La mayoría de los metafísicos convencionales coinciden en que ningún hecho empírico podría resolver quién tiene razón respecto a las cuestiones centrales de la metafísica. Sin embargo, niegan casi unánimemente que sus preguntas puedan responderse simplemente mediante un “análisis de conceptos”. Insisten en que se trata de preguntas sobre el mundo, no sobre nuestro lenguaje o nuestros conceptos. Esto nos deja con la pregunta: ¿cuál es la epistemología de la metafísica? ¿Cómo podemos esperar obtener conocimiento en metafísica?

Incluso aquellos que conservan la esperanza de que podamos llegar a saber qué puntos de vista son correctos, suelen reconocer las dificultades epistemológicas que surgen al intentar determinar cuál de ellos lo es realmente. Theodore Sider escribe: “una actitud sensata es que la metafísica, como gran parte de la filosofía, es simplemente difícil^[68]. Su epistemología también es ardua.” Y Ross Cameron añade: “la ontología no solo no es fácil: es muy, muy difícil^[69]”. Si bien podemos admirar la honestidad de estas afirmaciones, decir que algo es “difícil” no demuestra que el conocimiento de ese tipo sea posible, ni explica cómo podríamos esperar adquirirlo.

Compárese:

P: ¿Cómo se puede construir una estructura de madera en mar abierto?

Q: “Es muy, muy difícil.”

Casi todos los metafísicos serios que han abordado el problema epistemológico, y que han tenido como objetivo mostrar cómo podemos adquirir conocimiento en metafísica, han apelado simplemente a la idea de que nuestras formas de obtener conocimiento en este ámbito son paralelas a las de las ciencias empíricas. De este modo, la metafísica no enfrentaría un problema epistemológico especial. Como señala, “podemos comprender que los métodos empleados por los metafísicos son similares, módulo el cambio en el tema, a los métodos empleados por los científicos^[70]”.

En términos generales, la idea, popularizada por el argumento de David Lewis sobre los muchos mundos posibles, es que la teoría metafísica se confirma de la misma manera que las teorías científicas^[71]: “apelando a sus virtudes teóricas, como la explicación, la predicción y la repetibilidad”. Paul desarrolló una versión de este enfoque argumentando que “usamos desiderata teóricos como guías hacia la verdad en la ciencia”. Por lo tanto, se observan con frecuencia teorías metafísicas que se defienden apelando a su mayor simplicidad, unidad o poder explicativo en comparación con sus rivales, o bien porque sirven como parte de una inferencia a la mejor explicación^[72]. Los metafísicos a menudo toman estas virtudes como razones para pensar que sus teorías son verdaderas. Una vez más, Paul ofrece una versión de este punto de vista al concebir la metafísica como una disciplina dedicada al “modelado”, y argumenta que “una vez que se desarrollan los modelos metafísicos, al igual que en la ciencia, las teorías se comparan con respecto a la elegancia, la simplicidad y las virtudes explicativas de sus modelos, y se eligen sobre sus competidoras por inferencia a la mejor explicación”.

Por ejemplo, la discriminación que excluye de los puestos de trabajo a personas con antecedentes penales parece responder a un paradigma que solo empobrece y radicaliza el enojo de quienes la padecen. Melissa Burch aporta una luz teórica metafísica que sugiere que nuestra mejor esperanza para crear entornos laborales seguros no reside en la falsa promesa de la verificación de antecedentes, sino en la construcción de economías y comunidades que fomenten una seguridad real; por un lado, dispuestas a ceder algo de su privacidad de datos, y por otro, con gobiernos que puedan ser sancionados ejemplarmente si traicionan la confianza pública al aliarse con las bandas del crimen^[73].

En un sentido cauto, una primera preocupación es que las teorías metafísicas en competencia son, como reconocen sus propios defensores, típicamente empíricamente equivalentes. Como insisten los metafísicos, por ejemplo, no se puede establecer si existen universales platónicos o aristotélicos, o simplemente tropos de propiedad, señalando alguna diferencia empírica entre estas teorías. Tampoco se puede refutar a los eliminativistas acerca de los objetos ordinarios citando algún experimento u observación; decir “pero veo una mesa allí” no tiene fuerza probatoria, pues ellos responderán que lo que ves son partículas dispuestas según una cierta estructura en la tabla periódica. Por el contrario, en la ciencia incluso la equivalencia empírica aproximada es muy rara. Si en la metafísica solo se trata de virtudes teóricas distintas de la adecuación empírica al comparar teorías rivales, no está claro por qué deberíamos pensar que tales diferencias —en la simplicidad de la teoría, en su ontología o en su poder explicativo— sean realmente aptas para rastrear la verdad, en lugar de reflejar únicamente la utilidad de la teoría para criaturas limitadas como nosotros^[74]. Una preocupación relacionada, como ha argumentado extensamente Karen Bennett, es que, por lo general, las teorías metafísicas en competencia implican simplemente intercambiar una virtud teórica por otra, dejándonos a la deriva frente al objetivo de determinar qué teoría metafísica elegir. Paul reconoce que existe una diferencia de grado entre la indeterminación en la teorización científica y la metafísica, pero insiste en que esta diferencia no socava la capacidad de las virtudes teóricas para acercarnos a la verdad: si tales desiderata teóricos conducen a la verdad en la ciencia, también conducen a la verdad en la metafísica.

Pero incluso si uno está dispuesto a aceptar que las virtudes teóricas conducen a la verdad en las ciencias, y a vivir con una relativa indeterminación e incertidumbre en la metafísica, pueden surgir preocupaciones más profundas. Hay motivos para pensar que puede existir una diferencia no solo de grado, sino de tipo, entre las teorías metafísicas y las científicas, una diferencia que nos impide suponer que cualquier enfoque aplicable a las teorías científicas pueda trasladarse sin más a la metafísica. Michael Huemer examina cuatro explicaciones distintas del valor evidencial de la parsimonia en la teorización empírica y argumenta que ninguna de ellas se aplica a los casos filosóficos, lo que sugiere que, en contextos filosóficos típicos, la simplicidad ontológica carece de valor probatorio^[75]. 

Scott Shalkowski argumenta que la inferencia a la mejor explicación puede demostrarse empíricamente como un modo confiable de razonamiento cuando se trata de entidades observables, es decir, cuando existe la posibilidad de un acceso independiente que permita confirmar sus resultados. Sin embargo, esta fiabilidad se pierde cuando las conclusiones se refieren a hechos no observables^[76]. Shalkowski concluye que, aunque la inferencia a la mejor explicación funciona en los casos empíricos ordinarios que originalmente la motivan, hay pocas esperanzas de que pueda emplearse con éxito para resolver cuestiones metafísicas.

Juha Saatsi argumenta que existen diferencias de tipo en el uso de la inferencia a la mejor explicación dentro de la ciencia —ya se trate de afirmaciones sobre entidades observables o no observables— en comparación con su aplicación en la metafísica^[77]. Estas diferencias sugieren que la confiabilidad del método en la ciencia no puede trasladarse a la metafísica, dada la ausencia de retroalimentación empírica que oriente y evalúe nuestras prácticas explicativas en este ámbito. Por el contrario, en la ciencia sí es posible sostener la fiabilidad epistémica de las inferencias a la mejor explicación, tanto en el caso de los observables como en el de los no observables, precisamente porque existe un marco empírico que permite su corroboración o ajuste.

Pretendemos señalar que confiar en el paralelismo entre las apelaciones metafísicas y científicas a las virtudes teóricas plantea cuestiones mucho más amplias acerca de si dichos paralelismos realmente se mantienen y, además, si —incluso asumiendo que las virtudes teóricas distintas de la adecuación empírica conducen a la verdad en las ciencias— tenemos razones suficientes para pensar que ese mismo principio se traslada a la metafísica. Las respuestas habituales ofrecidas por los metafísicos resultan insuficientes para abordar lo que podría describirse como el problema del misterio epistemológico: la dificultad de justificar cómo nuestras teorías metafísicas podrían corresponder a la verdad en ausencia de mecanismos de contraste empírico.

4.11.1 El error es parte de la ecuación en la búsqueda del conocimiento

Somos agentes porque hacemos afirmaciones de conocimiento. Algunas de nuestras afirmaciones de conocimiento tienen éxito, otras fracasan. Las afirmaciones de conocimiento exitosas equivalen a conocimiento. En el contexto de la ciencia, donde las explicaciones de la estructura y el alcance del conocimiento se han formulado durante siglos, las teorías de la verdad y la justificación nos han permitido comprender cómo los sujetos pueden estar en contacto epistémico con cómo son las cosas en el entorno, a menudo llamado “mundo externo”. Por lo tanto, estas teorías nos guían hacia los bloques de construcción de la arquitectura del buen caso de hipótesis exitosas, o simplemente conocimiento.

Si bien las teorías de la verdad, la justificación y el conocimiento son considerados los máximos logros epistémicos, los fenómenos epistémicos negativos, como la ignorancia, el engaño, los errores, las confusiones, la incoherencia y el pensamiento falso, son mucho menos estudiados. Sin embargo, si se examinan más de cerca, resultan estar inextricablemente ligados a nuestra condición de sujetos capaces de hacer afirmaciones de conocimiento. Por lo tanto, necesitamos una teoría del pensamiento falso que esté anclada en una explicación de cómo tanto el pensamiento verdadero como el falso, el conocimiento y sus contrapartes abigarradas, pueden implementarse en la realidad real de las prácticas socialmente orquestadas y encarnadas a través de las cuales nosotros, animales con mentalidad específica, producimos conocimiento objetivo y compatible bajo condiciones falibles. En pocas palabras, tenemos que comprender la naturaleza de estar equivocados. Como señaló Aristóteles al comienzo de su Metafísica, los seres humanos están constitutivamente interesados en el conocimiento. Lo que siguió a esta declaración fue su propio relato de las diferentes formas de conocimiento. La forma más importante de conocimiento es lo que él, al igual que su maestro Platón, llamó “ciencia”, que no debe confundirse con la idea popular, aunque equivocada, de que los métodos científicos definitivos de las ciencias naturales son la única guía última para la verdad y la realidad.

“Conocimiento” o “ciencia”, como bien pensaban Platón y Aristóteles, son títulos para nuestro máximo logro epistémico. Son el resultado de afirmaciones de conocimiento, hechas y compartidas por humanos, que trascienden sus meras opiniones sobre cómo son las cosas al estar en contacto con éxito con una realidad que en gran medida no es de su propia creación.

Platón y Aristóteles se dieron cuenta muy pronto de que en las afirmaciones de conocimiento exitosas el pensamiento y el ser parecen fundirse. Lo que conecta el pensamiento y el ser en el logro del conocimiento es una forma particular de justificación o rendición de cuentas. Para resumir la historia, el conocimiento o la ciencia equivalen a una creencia verdadera no justificada accidentalmente, donde una creencia es un “tomar algo como verdadero”, y la justificación no accidental es lo que relaciona al sujeto cognoscente con los hechos, las verdades, que desea conocer.

En ese sentido, el conocimiento es simple, lo que no significa que conceptualmente no sea analizable. Unifica a un sujeto con una realidad en gran medida independiente de la mente a la que el sujeto dirige su intención en su afán de saber cómo son las cosas. A la luz de esta línea de pensamiento, entonces, el paradigma del conocimiento a lo largo de los siglos se convirtió en conocimiento proposicional de la forma “S sabe que p”. Aquí p se refiere a una proposición verdadera, o a un hecho, mientras que “sabe” se refiere a que el sujeto no se justifique accidentalmente tomando algo como verdadero.

Sin embargo, por simple y familiar que suene todo esto (al menos para los epistemólogos contemporáneos, que se centran en el análisis de los elementos del conocimiento provisional), el sujeto S que hace una afirmación de conocimiento, que puede ir bien (y equivaler a conocimiento) o fracasar (y equivaler a alguna forma de no saber), generalmente se deja fuera de la ecuación. Si el conocimiento es una creencia verdadera justificada no accidentalmente, entonces, ¿quién es el sujeto de una afirmación de conocimiento, y cómo se relaciona el caso de éxito del conocimiento con su portador falible?

Este es el punto ciego de la epistemología contemporánea al introducir un elemento en gran medida oxidado de la tradición filosófica. Si bien el conocimiento y la verdad son simples en el sentido de que estamos familiarizados con su análisis básico, sus contrapartes, la ignorancia, la falsedad y sus similares, son en su mayoría ignorados. Esto es aún más llamativo en una situación sociopolítica en la que la ignorancia, el negacionismo de los hechos, las noticias falsas, los sistemas digitales de manipulación, las redes sociales, la ideología, la propaganda, la ciencia ficción, las teorías conspirativas, los falsos juicios y todo tipo de ilusiones y engaños rondan la esfera pública.

Sin duda, recientemente ha habido muchos escritores filosóficos y sociólogos prominentes sobre los vicios epistémicos, el negacionismo, la ideología, la propaganda, la agnotología, la manipulación y la era de la posverdad en la política. Y, por supuesto, la psicología, la economía del comportamiento, la neurociencia y la filosofía han estudiado las ilusiones, los delirios, las alucinaciones, los prejuicios, el ruido y otros defectos fundamentales en el pensamiento, el juicio y la actuación. Sin embargo, lo que todavía falta es una visión conceptual de la conexión entre los modos multicolores de estar equivocado (la ontología de la confusión, los errores, la falsedad) y la teoría del pensamiento subjetivo encarnado, sin la cual no podemos comprender completamente el tema de las afirmaciones de conocimiento falible.

El propio Platón puso en el centro del escenario el problema de la falsedad y el error, tanto en su pensamiento sobre el conocimiento en el Teeteto como en su ontología en el Sofista, preguntándose cómo es posible estar equivocados. Para él, el problema de la falsedad y el no-ser están conectados, porque se dio cuenta de que nuestra capacidad para el pensamiento falso está ligada al hecho de que no necesariamente obtenemos la realidad o tenemos razón. Si bien el conocimiento presupone la inteligibilidad de equivocarse. Hacerlo bien, por lo tanto, no puede ser una fusión de pensamiento y ser que simplemente tiene lugar. De lo contrario, no podríamos pensar en el caso exitoso del conocimiento como un logro. Sería un mero evento mental sobre cuyo éxito no tenemos control y, por lo tanto, incompatible con la idea de un logos o un método que une el pensamiento y el ser juntos, haciéndonos responsables de nuestras creencias fuertemente arraigadas.

El estado mental del conocimiento es inmune a la revisión racional: no es falible. Sin embargo, esto no implica que quienes poseen conocimiento siempre sean capaces de hacer afirmaciones de conocimiento exitosas mediante la inspección de sus razones para sostener una creencia acertada. Hacerlo bien deja espacio para una posible duda (de segundo orden) sobre el estado mental de uno, incluso en los casos en que constituye conocimiento. Equivocarse, en cambio, es compatible con una actitud dogmática: se puede estar equivocado y estar completamente seguro de que no solo se aproxima a un grado mayor de verdad, sino que se asegura la propia pretensión de conocimiento por medio del mejor método disponible en un momento dado de la vida epistemológica de uno.

Desde los orígenes de la epistemología y la ontología, la verdad, el conocimiento y el ser se han comprendido mejor. Ha habido un progreso significativo en la teoría de la verdad proposicional, lo que ha dado lugar a impresionantes hazañas formales y técnicas que trascienden el ámbito de la producción de conocimiento académico. La inteligencia artificial no es más que, en última instancia, una articulación de nuestra visión de la arquitectura biológica de nuestro primitivo pero potente conocimiento de la razón, adquisición de conocimientos exitosos y controles lógicos de supervisión de errores de sesgo cognitivo.

Sorprendentemente, sin embargo, lo que falta es una explicación filosófica igualmente sofisticada de la falsedad, la ignorancia y otras deficiencias epistémicas. La teoría del pensamiento falso es parte integral de la teoría de la subjetividad, es decir, de una respuesta sistemática a la pregunta de quién es el sujeto en la formulación de una afirmación de conocimiento que conecta a alguien con los hechos que desea saber.

Así como la teoría del conocimiento (epistemología) va de la mano con una explicación asociada a las teorías de la verdad, la teoría de la ignorancia (agnotología) está inextricablemente ligada a una teoría de la falsedad o del error. La mera falsedad no es más que la contraparte de la verdad, es decir, la no verdad. Si pensamos en la verdad y la falsedad como propiedades de las proposiciones (lo cual es solo una parte de la verdad sobre la verdad y la falsedad), es sencillo (aunque no muy informativo) definir la falsedad simplemente como no-verdad. Dependiendo de la teoría más específica de la verdad de cada uno, la no-verdad equivaldría, por ejemplo, a la no correspondencia entre la sentencia y el hecho, entre la mente y la realidad; una forma de incoherencia; de disidencia irresoluble o simplemente una negación frente a una proposición reglamentada estipulada como verdadera. Sin embargo, esto no aclara qué significa que alguien esté equivocado. Pasa por alto el núcleo positivo de los fenómenos epistémicos negativos, como llamamos a los modos de estar equivocados.

El núcleo positivo de los fenómenos epistemológicos negativos es en sí mismo una forma de ser. El factor subjetivo ineliminable en el ámbito de las pretensiones de conocimiento confiere una solidez a los errores. Dado que los sujetos desean conocer y hacer afirmaciones de conocimiento, se encuentran en estados particulares cuando fracasan en su intento de obtener detalles en su entorno en gran medida independiente de la mente. Pero estos fracasos ciertamente no son irreales, y mucho menos intranscendentes. Acertar o equivocarse son a menudo cuestiones de supervivencia, lo cual es una de las razones por las que valoramos el conocimiento como el buen caso.

La teoría del falso pensamiento, del error y de la subjetividad está insertada en un marco teórico más amplio del que deriva los métodos desplegados, desde hace algunos años, se ha llamado marco de ontología de los campos de sentido (FOS^[78]). El principio básico de FOS es que existir es aparecer en un campo de sentido, Descartes lo expresó: primero pienso y luego existo. Nunca tratamos objetos aislados, sino siempre solo con objetos que forman parte de un contexto, sistema o dominio más amplio. Existir, entonces, es estar en un dominio o múltiples dominios, sobresalir entre otros objetos. Los objetos materiales existen como parte del universo, mientras que los números existen como partes de estructuras matemáticas que son, por su por su propia naturaleza, inmateriales. Otros objetos, como los objetos ficticios o imaginarios, existen en dominios o campos de sentido que dependen para su existencia de los actos mentales. En síntesis, el FOS parte de la idea de que existen una pluralidad de campos de sentido, que equivalen a una forma de pluralismo ontológico cuyos esbozos son el enfoque del sentido en la constitución de la realidad. Si la “realidad” es nuestro nombre preliminar para el dominio al que se dirige nuestro pensamiento cuando hacemos afirmaciones de concomiendo (un dominio que contiene ipso facto afirmaciones de conocimiento), uno puede leer el principio básico de FOS como apoyo a la afirmación de que al conocer y no saber, no producimos ni damos sentido a una realidad sin sentido. En todo caso, cuando entramos en la escena existencial y epistémica, encontramos un sentido que ya está ahí. En resumen, captamos el sentido, una idea encapsulada en la metáfora de un con concepto (significa aferrarse juntos).  

4.11.2 La realidad enmascarada inadvertida del pensador 

La última figura importante en la historia de la lógica y la epistemología que puso el dedo en la dimensión háptica del conocimiento como una especie de tacto entre nuestra base biológica  axiomática y una realidad, fue dada por Gottlob Frege^[79], a quien debemos la concepción moderna del sentido como un modo de presentación de los objetos.  En la estela de Frege, se pensaba que era una forma de captar un sentido. Sin embargo, nunca aclaró el sentido en el que el pensamiento podía ser la actividad de un pensador, ya que temía que traer al tema al sujeto socavaría la objetividad del conocimiento. Se equivocó en eso. En contraposición al propio realismo de Frege sobre el sentido y su explicación de la objetividad del pensamiento, argumentamos que nuestra única manera de comprender la falsedad es por medio de una teoría del error. Al equivocarnos, reconocemos la firma del sujeto en el espacio lógico. El falso pensamiento y la subjetividad son, por lo tanto, parte de nuestro camino hacia la realidad.

Una vez más, podemos motivar el interés en el fenómeno de estar equivocados remontándonos a un momento en la articulación original de Platón de la puesta en escena misma de la epistemología y la ontología. En un famoso símil en el Teeteto, se compara una afirmación de conocimiento con el intento de alguien de apoderarse del tipo correcto de pájaro en un aviario. Porque es posible no tener el propio conocimiento de esa cosa, sino tener algún otro conocimiento de atrapar algún otro conocimiento, entre los que vuelan por ahí, uno falla y se apodera de uno en lugar del otro. Es entonces cuando uno piensa que once son doce, habiendo conseguido el conocimiento de doce, es como uno podría apoderarse de una paloma en lugar de un gorrión.

En nuestra analogía, el tipo correcto de pájaro sería un pensamiento verdadero, mientras que el tipo incorrecto de pájaro sería un pensamiento falso. La posición del sujeto es una en la que estamos suplicando por agarrar un objeto en movimiento en un entorno del que nosotros mismos formamos parte, en forma de animales mentales. Una suposición de objetividad, que dice que ser alguien, ser sujeto, ser agente, es estar equivocado sobre algo. Conseguir que algo llegue con éxito a la visión epistémica solo puede realizarse bajo condiciones de estar equivocados en algún lugar de nuestro sistema de creencias. Ser un pensador falible significa estar sujeto a una ignorancia constituida y a menudo de amplio alcance en cuanto a cuáles de nuestras creencias son realmente verdaderas y cuáles falsas. Ser sujeto es estar equivocado acerca de algunas cosas sin estar en posición de establecer de una vez por todas cuáles de nuestras creencias son no accidentalmente verdaderas y por lo tanto constituyen conocimiento. Por esta razón, incluso nuestros estados mentales factivos (epistémicos exitosos) están incrustados en el despliegue de la realidad mental que están integrados en nuestra red de creencias y por lo tanto, de una forma u otra, ligadas a falsas creencias sin que el sujeto esté nunca en condiciones de aislar los casos buenos de los malos.

Esta tesis raya en lo obvio simulamos toda nuestra red de creencias, como dice el refrán de los pájaros. Sin embargo, defenderemos una afirmación más fuerte según la cual nunca hay un episodio completamente aislado de un sujeto individualizado que simplemente capta P y no la cree accidentalmente, de modo que sabe que P sobre la base de su comprensión completamente clara de P. Si observamos la implementación real de la afirmación de conocimiento en la vida del sujeto, pronto veremos que su justificación general para la afirmación de conocimiento en algún momento se queda corta con respecto al conocimiento. Esto no significa que no sepa lo que sabe, sino que su estado mental realmente implementado está incrustado en la estructura de campo difusa, temporal, no proposicional, y sin sentido a la que ella, como sujeto tal, pertenece.

Por lo tanto, lo que somos como sujetos se caracteriza mejor en vista de los límites de nuestro conocimiento objetivo individual y compartido actual. Nuestros estados mentales generales son fundamentalmente confusos, consistiendo en pensamientos verdaderos y falsos. Esto no significa que no podamos acertar: el falibilismo no es una forma de escepticismo según el cual el conocimiento es imposible debido a algún factor subjetivo u otro. Más bien, el falibilismo es un elemento indispensable en cualquier concepción realista de la adquisición de conocimiento. Pertenece al ámbito de la heurística, cuya teoría sería irresponsablemente incompleta si olvidáramos proporcionar una comprensión reflexiva de nosotros mismos como sujetos de reclamación de conocimiento.

La teoría falibilista de la subjetividad del conocimiento resulta justamente de la idea de que el conocimiento es nuestro concepto del caso de éxito de las afirmaciones de conocimiento. Saber algo es acertar por las razones correctas (es decir, no accidentales). Si un sujeto realmente acierta en realidad, no tiene sentido pensar en este estado mental en particular como potencialmente incorrecto. Dicho esto, el conocimiento del sujeto no contaría como un logro si no hubiera sido posible que el sujeto se equivocara. Esto trae el concepto de una afirmación de conocimiento falible que conceptualmente precede a la del conocimiento como el caso de éxito paradigmáticamente epistémico. El portador de la falibilidad, en este contexto, no es el conocimiento ni la pretensión de este, sino el sujeto cuya actividad de adquisición de conocimiento se despliega como parte de su vida mental. Tan pronto como pensamos en el conocimiento y en las afirmaciones de conocimiento como partes de la vida mental más amplia de los sujetos, tenemos a la vista la realidad de estar equivocados. Esto no le hace el juego al escéptico, en el sentido de un conjunto de argumentos y paradojas diseñadas para demostrar que el conocimiento es imposible debido a alguna deficiencia u otra en la naturaleza de la justificación, no puede ser motivado sobre la base de la idea misma de falibilidad solamente.

La afirmación específica sobre la falibilidad que corre como un hilo a través de noción de que la subjetividad es parte de animales de mente especifica. En el caso de los animales capaces de afirmaciones explícitas de conocimiento, estamos tratando con animales humanos. La vida mental de los animales que somos se despliega en forma de conciencia subjetiva. La conciencia dada en términos  una ontológia realista de los sentidos y del sinsentido. Esto conduce, a través de la explicación del error, a una contribución a un tema fundamental en la filosofía de la mente en la intersección de la ontología y la epistemología, es decir, la conciencia y su relación con la autoconciencia.

Argumentamos que en el realismo del sentido, es un error pensar en al cosmos como algo con sentido, pensamiento y propósito. No se debe asignar ninguna prioridad metafísica u ontológica a un mundo sin espectadores que existió durante eones antes de la evolución de los sujetos que conocen y actúan con la capacidad de hacer explícita su propia creación de sentido en un “exilio del cosmos” que de otro modo carecería de sentido. El sinsentido ontológico es una forma de confusión de campo que se manifiesta en el paradigma de la ciencia como una ilusión que existe objetivamente. La cuestión del sinsentido se distinguirá de las discusiones sobre la mera falta de sentido a raíz de los intentos de Carnap, Wittgenstein y otros más recientes de aclarar la relación entre enunciados, sentencias, proposiciones, cláusulas y pensamientos lingüísticos y semántica significativa.

El despliegue espacio-temporal de la realidad y nuestra posición subjetiva en esta evolución no pueden reducirse a nuestra posición proposicional como conocedores de hechos atemporales y estructurales en los que están incrustados objetos bien definidos. El sinsentido queda relegado del ámbito de los supuestos errores de categoría o ilusión semántica a una categoría por derecho propio, que da cuenta de la presencia real de esos sujetos entre sus objetos. De esta manera, la distinción sujeto-objeto sigue siendo un dispositivo funcional para articular una teoría sin sucumbir a la tentación de inflar sujeto y objeto en un dualismo metafísico de dos entidades.

Ser alguien, un sujeto particular o un pensador individual, es estar equivocado acerca de indefinidamente muchas cosas, incluyendo hechos en los que un determinado objeto de conocimiento está incrustado. Saber algo o saber que algo es el caso no tiene por qué implicar una comprensión completa del objeto o del hecho en cuestión. Nuestras afirmaciones de conocimiento son y siguen siendo falibles debido a su integración en nuestra forma de vida como sujetos. Por lo tanto, el tema correcto de una teoría de la subjetividad no es la autorreferencia, mediante la cual aparentemente llegamos a comprender nuestra propia mera existencia como pensadores. Por el contrario, el hecho relevante sobre nosotros mismos que da cuenta de nuestra subjetividad es la realidad altamente heterogénea de estar equivocados.

4.12 Poetas y científicos en la búsqueda de sentido 

Somos sujetos, agenciamos información. Entre otras cosas, esto significa que experimentamos la realidad desde una perspectiva o punto de vista cambiante en virtud de estar arraigados en su despliegue temporal. Estamos, pues, en contacto con una realidad que, de un modo u otro, siempre difiere de la forma en que la representamos. Esta característica, la subjetividad, no se limita a la percepción consciente y vigilante, cuya línea de visión puede integrarse en modelos perspectivos para que podamos distinguir entre la forma de nuestra representación y la realidad que podemos captar a través de ella y en ella. Los objetos cuyas propiedades procesamos en modalidades sensoriales distintas de la vista se nos presentan igualmente desde el punto de vista humano; como dijo Immanuel Kant, los sonidos indican la ubicación y otras propiedades de una fuente distante de nosotros y los sentidos químicos (olfato y gusto) no solo nos informan de manera opaca sobre las propiedades químicas de los objetos con los que estamos en contacto. Más bien, nos gusta o nos disgusta un sabor y un olor, y nos presentan características de la realidad.

A través de la percepción, los sujetos aprenden algo tanto sobre su entorno como sobre su posición dentro de él. Cada modalidad sensorial presenta objetos que están incrustados en el estado de cosas más amplio, como si fueran de cierta manera. En la medida en que estos objetos se nos aparecen, irradian los sentidos como modos de presentación o sentidos. La noción de los sentidos como forma de situar los objetos en relación tanto con los sujetos como con otros objetos será el enfoque que adoptamos. Los objetos irradian sentido (estructuras de información) en la forma en que se nos aparecen en nuestra relación perceptual y epistémica con ellos. En este contexto, tal como lo recordó Frege (a quien debemos la noción de los sentidos como modos de representación de los objetos), no debemos reducir los sentidos como modos de presentación de los objetos a estados subjetivos que bloquean los objetos mismos de la vista. No son meramente vehículos psicológicos de conocimiento de nuestros propios estados subjetivos, sino modos de estar en contacto con cómo son realmente las cosas. A esos sentidos los llamamos sentidos objetivos.

Un enfoque en el que el papel del sentido y los sentidos como modos de captación de la realidad que son a su vez parte de ella. En este contexto, estamos a favor de un tipo de realismo sobre los sentidos según el cual los sentidos son propiedades de las cosas mismas o formas de que las cosas sean: los objetos se presentan como tales y, por lo tanto, nunca son meramente una ilusión. Dicho esto, el reino de los sentidos no se agota con los sentidos objetivos. También hay sentidos subjetivos, es decir, sentidos que involucran constitutivamente a un sujeto. Un sujeto es un conocedor falible, alguien cuyas capacidades epistémicas (desde el registro sensorial no consciente de bajo nivel hasta el nivel más alto de autoconocimiento) en un momento u otro siempre se quedan cortas para acertar. Un sujeto es alguien que se equivoca en algo, incluso en un escenario en el que hace tan bien como puede. Los pensadores falibles, es decir, los sujetos de las afirmaciones de conocimiento, están constitutivamente equivocados sobre algunas cosas, incluso en escenarios en los que aciertan en algo. Para los sujetos de conocimiento, pretensiones de aprehensión de la realidad significan estar en contacto falible con cómo son las cosas.

Un poeta:

Todos nosotros sabemos preguntar a los pintores sobre la luz del sol en su girasol, unas botas viejas, caballos...; un niño puede preguntar por la música de Mozart, preguntar al barbero sobre el cambio climático; un hombre apoyado en su novia puede preguntar sobre lo revolucionario del sabor y aroma del café. Pregúntale al hombre que sufre hambre; pregúntale a la mujer sobre la violencia. Pregúntale al pájaro azul que vuela cada noche. Pregúntale al científico sobre sus datos de la realidad, si son correctos a pesar de que los conceptos que les dan sentido son solo lenguaje. Pregúntale a las piedras y a los pastos sobre los que caminas qué son. Pregúntale a las predicciones de la mecánica cuántica por qué el mundo es así y no de otra forma. Pregúntale a un político por qué mentir es su mayor recurso. Pregunta al rostro que ves a la luz del día. Pregunta a los condenados, a los necios de la verdad supuesta absoluta, a los esclavos de los dogmas. Pregúntale a tu propia sombra que dibuja un mapa de tus átomos. Lo real es mudo, un silencio exquisito para los exploradores de la causalidad.

Partimos de observaciones de que no conocemos ni podemos conocer una realidad sin sentido para nuestra racionalidad, es decir, una realidad que no fuera de cierta manera presentable para los pensadores. Un pensador es simplemente alguien que capta la realidad en términos de cantidad, geometría, categorías, probabilidad causal y lógica. Una modalidad sensorial es una manera de estar en contacto falible con la realidad, y el nombre más general para tal contacto es pensar, es decir, comprender cómo son las cosas en términos de que son de cierta manera. A la luz de estas consideraciones elementales, asumimos que los sentidos como modos de presentación de objetos y formas de ser no están simplemente “ahí afuera”, al menos no en general. Están “aquí adentro”, es decir, donde estamos ubicados como pensadores, así como están “allá afuera”, más allá de nuestra piel. Ojos, olfato, gusto, afecto llegan a ser la superficie más externa en lo que sigue, los sentidos abarcan tanto el sentido objetivo (al que se refiere Frege) como el sentido subjetivo, es decir, modalidades sensoriales que están ligadas a la presencia de pensadores encarnados a quienes los objetos se les presentan de cierta manera. El sentido y los sentidos están entrelazados. El sentido subjetivo es el sentido procesado por los sujetos de tal manera que necesitan comprender la contribución del sujeto a su contenido para poder captar sentido. El sentido objetivo es el sentido para el cual no es así; se involucran fundamentos de lo real, instrumentos, se generan datos en diseños experimentales controlados, se evalúan bajo leyes lo contrafactual (lo sintético en lo real), y sobre todo, las matemáticas son el lenguaje para ello.

4.13 El escepticismo metodológico

Instrumental: no es una posición final, sino un medio para alcanzar conocimiento cierto.

Racionalista: confía en la razón como el camino hacia la verdad.

Crítico: exige que todo conocimiento sea justificado racionalmente.

Fundacionalista: busca una base firme para reconstruir el edificio del saber.

A diferencia del escepticismo metodológico, el dogmatismo negativo desarrolla argumentos destinados a obtener resultados específicos: una postura que niega de manera definitiva la posibilidad del conocimiento verdadero, pero sin cuestionar su propia negación; es decir, convierte esa negación en un nuevo dogma. “No podemos conocer nada con certeza” —afirmado como una verdad indiscutible. Esta actitud se compromete con la obtención de conclusiones que clausuran la pregunta, en el sentido de que ya no se puede afirmar un conjunto o categoría de pretensiones de conocimiento a las que antes accedíamos como si fueran un derecho no problemático e incondicional.

Por el contrario, el escepticismo metodológico (pienso, luego existo) se expresa a través de paradojas: argumentos construidos a partir de premisas y reglas de inferencia aparentemente aceptables que, sin embargo, conducen a conclusiones evidentemente insostenibles. Las paradojas constituyen una clase peculiar de razonamiento: aunque se ajustan a las condiciones de la racionalidad, por una variedad de razones generalmente no podemos aceptar sus conclusiones. En cambio, nos vemos obligados a disolverlas.

Una distinción que muchas veces se diluye en los discursos contemporáneos: la diferencia entre dudar como forma de apertura y negar como forma de clausura. El dogmatismo negativo que denunciamos es, en efecto, una inversión sombría del dogma clásico: ya no pretende afirmar verdades absolutas, sino negar de forma absoluta la posibilidad de verdad. Pero en ambos casos, lo que se pierde es la capacidad de escucha, la disposición a la interrogación paciente, el coraje de habitar lo incierto sin volverlo consigna. El escepticismo metodológico, en cambio, mantiene vivo el espíritu de la filosofía: no se limita a denunciar la insuficiencia del conocimiento, sino que muestra la necesidad de cuidarlo, afinarlo, y sobre todo, no convertirlo en dogma ni siquiera cuando se trata de negar. Porque en última instancia, pensar no es concluir, sino mantener abierta la posibilidad de otro comienzo.

El escepticismo metodológico ofrece una lección sobre la finitud de nuestro conocimiento. Muestra que, dado que no tenemos acceso reflexivo al conjunto que comprende la totalidad de las condiciones de posibilidad de nuestro saber, todo conocimiento depende continuamente de que se cumplan condiciones que están más allá de nuestro control racional. Logra este efecto señalando que no podemos excluir racionalmente los escenarios escépticos en la reflexión epistemológica explícita, porque el conjunto de escenarios de este tipo es infinitamente grande. Claramente, si saber algo presupone que, primero, dejemos fuera algunas variables por considerarlas arbitrariamente poco significativas, entonces este tipo de escenarios se multiplica sin límite. Y si saber algo presupone que podemos excluir todos los escenarios escépticos uno por uno, trabajando a través de ellos de manera fragmentaria, difícilmente podemos proporcionar una garantía sólida de que sabemos algo en absoluto. Este pasaje pone de relieve una verdad filosóficamente incómoda: la aspiración de certeza absoluta no sólo es ilusoria, sino que puede ser epistemológicamente contraproducente.

Sin embargo, esta dificultad de ninguna manera nos da derecho a inferir que no tenemos conocimiento empírico, suponiendo que tal derecho cancelaría inmediatamente las condiciones de posibilidad de la teoría de la epistemología, al destruir todos sus objetivos; es decir, el conocimiento de primer orden en su conjunto. El conocimiento de primer orden se refiere, en términos generales, al conocimiento directo o inmediato de un objeto, hecho o situación, sin necesidad de reflexión metacognitiva o evaluación sobre ese conocimiento.

El escepticismo metodológico formula paradojas, argumentos con conclusiones insostenibles. Pero estas conclusiones son insostenibles precisamente en virtud de las condiciones reflexivas de la epistemología. En pocas palabras, las paradojas terminan por abolir la epistemología misma y cualquier inferencia que pueda extraerse sobre la sostenibilidad del conocimiento empírico.

El problema no es, como podría parecer a primera vista, simplemente el cuestionamiento de si podemos saber algo en absoluto, ni que el escepticismo metodológico amenace nuestro conocimiento de primer orden. El problema es más bien que la abolición de nuestro conocimiento de primer orden conduce a la abolición de la epistemología misma, que inicialmente habíamos introducido como teoría reflexiva de ese mismo conocimiento.

Si eliminamos la posibilidad de conocimiento empírico desde la radicalidad escéptica, no solo perdemos acceso a lo real, sino que también dejamos sin fundamento a la epistemología como empresa teórica. Es un movimiento en el que el pensamiento se vuelve contra sí mismo y se autodevora, al negar la legitimidad de las condiciones mismas que lo hacen posible. Esta paradoja es el corazón del escepticismo metodológico, pero también su límite: no puede derribar la estructura sin demoler su propia plataforma. 

4.14 Paradoja de la humildad intelectual y la valoración de la ignorancia

Cuando el poeta y diplomático inglés Matthew Prior (1664-1721) imaginó un diálogo entre John Locke y Michel de Montaigne a finales de la década de 1710, este último llevaba muerto más de un siglo y el filósofo inglés casi quince años, creo la paradoja del “vulgo”, la ignorancia equivaldría en ese momento a algo vulgar^[80]. Los dos hombres no solo habían vivido en diferentes países, sino que también habían conocido diferentes contextos religiosos y políticos, y por tanto, presumiblemente habían construido sus filosofías a partir de diferentes fuentes. Este diálogo les dio a Prior la oportunidad de celebrar a su campeón francés en detrimento del filósofo inglés, pero la elección de Locke como interlocutor de Montaigne no fue arbitraria. La filosofía de Locke fue muy elogiada en el momento en que Prior escribió sus diálogos, tanto en Inglaterra como en Francia, pero sobre todo, los dos pensadores habían propuesto actitudes hacia el conocimiento que Prior consideraba contradictorias. Así, Locke fue presentado como un racionalista en la línea cartesiana, mientras Montaigne fue presentado como un empirista pragmático (el conocimiento es un proceso continuo de interacción con el mundo y de ajuste de nuestras creencias en función de las experiencias y los resultados prácticos) sobre el modelo inglés. Esas relaciones con el conocimiento y las formas de conocer también implicaban relaciones específicas con la ignorancia, al abordar el aprendizaje, o la ausencia de él, de los lectores a los que se dirigían esos hombres y el papel de la ignorancia en el descubrimiento, la invención y, más en general, el avance del conocimiento y la ciencia. De hecho, en el diálogo de Prior, Montaigne reprende a Locke por su desprecio por “lo vulgar” y se burla de su obsesión por el método y el autoconocimiento.

El señor francés, sin embargo, se enorgullece tanto de dirigirse a los ignorantes como de ser ignorante él mismo, afirmando la paradójica superioridad del “vulgo” sobre el erudito: “los vulgares son los únicos eruditos”. En otras palabras, los analfabetos, entendidos como hombres que no han sido educados en la escuela pero que pueden poseer conocimiento práctico, como los artesanos y los campesinos, deben ser celebrados por los descubrimientos más importantes jamás realizados, como la pólvora y la imprenta, y Locke se equivoca al pensar que debe dirigir sus escritos a los eruditos. Pero la acusación de Montaigne -o mejor dicho de Prior- es injusta, ya que el filósofo inglés reconoció y elogió el ingenio de los artesanos, como lo atestigua claramente su ensayo sobre el entendimiento humano de 1690: “era al estadista artesano, a quien los gobiernos del mundo debían su paz, defensa y libertades; y del analfabeto y despreciado por ser pobre (un hombre de vergüenza) que recibieron los perfeccionamientos de las artes útiles”. Así, a pesar de los esfuerzos de Prior por hacer pasar a Locke como un filósofo que despreció al vulgo y a Montaigne como un hombre humilde que se identificó con el vulgo, la verdad es que ambos pensadores, entre muchos otros en la Edad Moderna, celebraron a los inventores y descubridores analfabetos, como si su propia ignorancia los hiciera más propensos que los eruditos a contribuir al avance del conocimiento.

interpretaciones de la noción de ignorancia que podrían justificar tal inversión de significado en Inglaterra y Francia en tiempos de Montaigne y Locke (1580-1700). En otras palabras, la humildad intelectual examina las valoraciones de la ignorancia expresadas en el siglo XVII y muestra que, a pesar de haber sido atacada como algo vulgar, esas celebraciones estaban lejos de ser marginales, hasta el punto de que se puede decir que las primeras doctrinas modernas de la ignorancia contribuyeron a la aparición de nuevas formas de conocimiento. Por lo tanto, el concepto de humildad intelectual afirma que la noción de ignorancia debe ser reinstalada en la historia intelectual de principios del período moderno como uno de los temas conceptuales más importantes de la época. Para hacer este argumento, aquí se identificaron y desarrollaron las virtudes de la ignorancia transmitidas en los discursos filosóficos y religiosos modernos tempranos: primero, la ignorancia podría verse como conducente a la sabiduría y al autoconocimiento; en segundo lugar, podría comprenderse como un principio de conocimiento, es decir, una condición que permite el acceso directo a la verdad; y tercero, llegó a ser interpretada por varios filósofos naturales como un instrumento epistemológico que ayuda a desarrollar nuevos métodos.

¿Cómo funciona la inteligencia humana en términos de hacer y de los distintos tipos de respuestas frente al acto de pensar? ¿Qué principios matemáticos y bloques de construcción computacionales pueden explicar nuestra capacidad para dar sentido al mundo y a nuestro lugar en él? Estas son preguntas fundamentales, las mismas que originalmente nos trajeron, a nosotros y a muchos otros, a la ciencia cognitiva. Su origen se remonta a los primeros intentos de modelar el pensamiento humano como una especie de computación adaptativa, con vínculos a ideas filosóficas que datan de mucho antes, por ejemplo, las de Hume, Kant y Mill.

Eli de Gortari disertó en “La ciencia en la historia de México”, la siguiente revolución para el crisol de pensadores sería la llamada "ciencia de la racionalidad^[81]"; un nuevo vigor de tradición científica reflejado en las aulas, la literatura, la investigación y la divulgación cultural. Sin embargo, estas grandes preguntas pueden parecer imposibles de abordar con claridad en un contexto de cambio de paradigma. ¿Cómo sabríamos si hemos dejado atrás nuestra pereza cognitiva, si tenemos razón o, al menos, si estamos en el camino correcto?

Podemos empezar con una pregunta más manejable y tal vez más fascinante en cuanto a sus posibilidades de respuesta: ¿cómo es que nuestras mentes logran obtener tanto a partir de tan poco? En todos los dominios donde observamos la mente en acción, notamos un desajuste entre la información que llega a través de los sentidos y los resultados de la cognición. Construimos modelos causales ricos del mundo, hacemos generalizaciones sólidas, creamos abstracciones poderosas e incluso inventamos mundos completamente nuevos y formas de entenderlos, todo ello mientras los datos de entrada son escasos, ruidosos, incompletos y ambiguos, y en muchos sentidos, excesivamente limitados. ¿Cómo lo logramos?

Esta es la pregunta que motivó las primeras investigaciones en ciencia cognitiva. El desafío que plantea, junto con lo que podría considerarse una solución satisfactoria, puede concretarse y precisarse con algunos ejemplos conocidos. Considere, primero, la situación de un niño que aprende el significado de las palabras. Un niño típico de dos años puede aprender a usar una nueva palabra como "gato" o "agua" tras observar solo unos pocos ejemplos, y, a veces, incluso un único ejemplo es suficiente^[82]. Sabemos que comprenden el significado de estas palabras, y no solo los sonidos, porque pueden generalizarlas: son capaces de usar las palabras de manera adecuada en situaciones nuevas. Así, emplean estas palabras categóricamente para referirse a cualquier entidad que pertenezca al tipo correspondiente.

Esta es una hazaña notable, vista en términos de computación o inferencia estadística. Dentro del espacio infinito y probablemente de dimensiones infinitas de todos los objetos posibles, hay un subconjunto infinito, pero mucho más pequeño y altamente restringido, que se llama “gato”. Y otro para “cepillos para los dientes”. ¿Cómo comprende el niño los límites de estos subconjuntos al ver solo uno o unos pocos ejemplos de cada uno? ¿Y cómo podría una máquina aprender a hacer lo mismo? Los enfoques algorítmicos convencionales de la estadística y el aprendizaje automático suelen requerir decenas o cientos de ejemplos etiquetados para clasificar los objetos en categorías y no generalizan de forma tan fiable o sólida. ¿Por qué les va mucho mejor a los niños? Los adultos se enfrentan con menos frecuencia al reto de aprender conceptos de objetos completamente nuevos, pero pueden ser igual de buenos en ello: compruébelo usted mismo con los objetos generados por ordenador.

Fundamentalmente, el mismo desafío se encuentra en todos los aspectos de la cognición. Consideremos, por ejemplo, los rompecabezas y juegos que niños y adultos descubren y aprenden por sí mismos. Simplemente observando un juego de mesa, es improbable que una persona aprenda todo lo necesario para jugarlo con habilidad. Sin embargo, bastan unas pocas rondas de acción para inferir gran parte de las reglas: qué movimientos están permitidos, cuáles son sus efectos en el estado del juego, y tal vez incluso hacia qué objetivos parecen apuntar. Estas inferencias, aunque sean conjeturas y contengan cierta incertidumbre o errores, serían mucho más precisas que cualquier suposición hecha sin haber observado las jugadas. Además, basta un minuto de observación para deducir las reglas y objetivos de muchos juegos populares infantiles, como las damas o la rayuela.

Este es, esencialmente, el problema de la generalización a partir de datos dispersos. Es el mismo problema que enfrenta un niño cuando aprende a usar nuevas palabras o a participar en un juego de patio, observando lo que hacen y dicen los demás. Una vez que se reconoce este desafío, se hace evidente que aparece en todas las facetas de la cognición. Este fenómeno surge en el aprendizaje de aspectos fundamentales del lenguaje, como la sintaxis o la morfología de una lengua materna. También se manifiesta de forma cruda en el aprendizaje causal: aunque toda clase de estadística enseña que la correlación no implica causalidad, incluso los niños pequeños pueden inferir de manera sorprendentemente confiable vínculos causales a partir de un puñado de eventos. Estas muestras son demasiado pequeñas para calcular correlaciones significativas con métodos estadísticos tradicionales, pero no para la capacidad cognitiva humana.

Quizá las formas más profundas de generalización en el aprendizaje humano ocurren a lo largo del desarrollo cognitivo, en la construcción de sistemas de conocimiento a mayor escala: teorías intuitivas de la física, la psicología o la biología, o sistemas de axiomas en la estructura del juicio. La construcción de estos sistemas puede llevar años, mucho más que aprender una sola palabra nueva, una conexión causal novedosa o las reglas de un nuevo juego. Sin embargo, también a esta escala, el producto final del aprendizaje supera con creces los datos observados, aunque solo sea porque los conceptos mentales de estas teorías, como el peso y la densidad, las creencias y las preferencias, o la muerte, no son observables en absoluto^[83]. ¿Cómo desarrollan los seres humanos la capacidad de razonar? La investigación de Susan Careyny colegas: “sus datos convergen con evidencias previas que no encuentran una capacidad para representar la negación en bebés menores de 15 meses de edad y entran en conflicto con otras evidencias de diferentes paradigmas que sugieren que los bebés sí tienen esta capacidad^[84]”.

Una teoría intuitiva también puede ser transformada en un instante, modificada para acomodar la posibilidad de nuevas leyes causales con solo una pizca de evidencia sensorial, si es la astilla correcta. Pensemos en un niño que ve imanes por primera vez, o un mando a distancia, un dispositivo de pantalla táctil o una máquina antigravedad. Una sola demostración es suficiente para sugerir que el mundo podría funcionar de manera diferente a como lo había pensado anteriormente; uno o dos experimentos más, jugando con el nuevo sistema por sí mismo, confirman esa sospecha. Por supuesto, los científicos humanos aún no han inventado una máquina antigravedad, pero puedes apostar que, si lo hacen y está disponible para que cualquiera la compre y juegue con ella en casa, los niños humanos aprenderán sobre sus efectos dramáticos en poco tiempo, a partir de los mismos patrones mínimos de datos.

Tratar de resolver el problema de cómo obtenemos tanto de tan poco no es, de ninguna manera, el único punto de partida interesante para construir modelos de la mente, pero es sin duda uno de los más centrales, con muchas otras preguntas interesantes que surgen de los intentos de responderlo de manera convincente. Pone al descubierto los grandes desafíos a los que se enfrenta cualquier intento de comprender la inteligencia como la solución a un conjunto de problemas matemáticos y computacionales. Esto es oportuno, ya que las tecnologías de inteligencia artificial (IA) de hoy en día están cada vez más impulsadas por marcos de aprendizaje automático que están infinitamente hambrientos de datos y desesperadamente dependientes de ellos. Generalizar más allá de los datos observados está en el corazón de la dificultad de construir máquinas con algo que se parezca a la inteligencia humana. Y es un desafío atemporal.

Los filósofos han reflexionado sobre versiones de esta pregunta durante dos mil años, la más famosa como “el problema de la inducción”, conocido en la versión de David Hume, pero con raíces que se remontan a Platón y Aristóteles y que abarcan toda la tradición filosófica occidental^[85]. El desafío del siglo XIX inspiró a generaciones de pensadores sobre el pensamiento cuando escribió en un sistema de lógica: ¿Por qué un solo caso, en algunos casos, es suficiente para una inducción completa, mientras que en otros, miríadas de casos concurrentes, sin una sola excepción conocida o supuesta, recorren tan poco el camino hacia el establecimiento de una proposición universal? Quien pueda responder a esta pregunta sabe más de filosofía de la lógica que el más sabio de los antiguos, y ha resuelto el problema de la inducción^[86].

Mill estaba escribiendo sobre el problema de la generalización tal como lo enfrentan los científicos que observan su mundo, pero también podría haber estado hablando de nuestro problema moderno de generalización en la ciencia cognitiva: fuera de la amplia gama de formas posibles en que los estudiantes humanos podrían ir más allá de los datos proporcionados, ¿cómo sabemos, a veces a partir de un solo ejemplo, cuáles de estas generalizaciones deben sostenerse y cuáles no? Muchos han profundizado en estas preguntas y continúan impulsando debates sobre los orígenes del conocimiento en la epistemología contemporánea y la filosofía de la ciencia^[87].

¿Cómo podemos llegar a comprender las leyes del universo u otras propiedades perdurables del mundo? ¿Qué significa una ley de la naturaleza o una propiedad perdurable? ¿Cuál es nuestra verdadera base de confianza para creer que una ley o un concepto universal que ha sido válido en todas partes y siempre no será falsificado mañana o el próximo año?

En 1956, cuando la IA y la ciencia cognitiva apenas comenzaban a emerger como campos de estudio, Popper escribió que eligió estudiar los orígenes del problema de la epistemología cotidiana: el problema de los orígenes del conocimiento de sentido común, escrito a gran escala^[88]. En la época de Popper, como en la de Mill, el conocimiento científico era quizá más fácil y convincente de estudiar que el conocimiento de sentido común. Vemos la misma analogía ahora, pero a la inversa. Elegimos estudiar la comprensión de sentido común del mundo por parte de la mente humana y cómo opera a través de los saltos inductivos cotidianos, porque expone los problemas más profundos de los orígenes y el crecimiento del conocimiento en su forma más manejable y urgente. En este momento, con las herramientas matemáticas, computacionales y experimentales de las que disponemos, esta es la forma del problema clásico de la inducción más susceptible de una explicación científica rigurosa y del progreso práctico de la ingeniería.

Las respuestas que los filósofos han dado a los problemas de la inducción se remontan a Platón. Si la mente va más allá de los datos dados, alguna otra fuente de información debe compensar la diferencia. No puede haber almuerzo gratis, ni magia, ni algo a cambio de nada en una explicación computacional o de procesamiento de información de la cognición. Esta idea se formaliza en los teoremas de "no almuerzo gratis" para el aprendizaje automático; por ejemplo, algunos conocimientos previos más abstractos deben generar y delimitar las hipótesis que los aprendices consideran, o sería imposible una generalización significativa^[89]. Los neurocientíficos que hacen preguntas análogas sobre cómo la percepción interpreta las entradas sensoriales ruidosas hablan de los “modelos internos” del cerebro. La terminología varía, pero siempre describe algún tipo de modelado del mundo que llena los vacíos de la experiencia, permitiendo que nuestras mentes conviertan racionalmente los datos en creencias confiables y razonables.

Esta “respuesta” no es realmente una respuesta, por supuesto, sino más bien una invitación a hacer más preguntas y una guía sobre dónde deben enfocarse. Para una explicación de ingeniería inversa, las preguntas clave ahora se centran en explicar la naturaleza, las funciones y los orígenes de este conocimiento abstracto en términos computacionales: ¿cómo resuelven exactamente el problema de la inducción?, ¿cuál es su forma y contenido específico?, ¿y cómo surge en las mentes y cerebros humanos?

Otra manera de decirlo sería: ¿cómo guía el conocimiento abstracto la inferencia a partir de datos empobrecidos para producir generalización, predicción y decisiones confiables y valiosas? ¿Qué forma adopta ese conocimiento y qué contenido informativo tiene en varios dominios del pensamiento? ¿Cómo crece el conocimiento a lo largo de la vida, equilibrando la necesidad de una fuerte restricción con la flexibilidad de aprender continuamente sobre nuevos dominios?

Además, ¿de qué manera el conocimiento que construimos guía nuestra planificación y acción en el mundo? ¿Cómo lo ponemos en práctica? ¿Cómo se implementan realmente los algoritmos y las estructuras de datos necesarios para representar, adquirir y desplegar el conocimiento a escala humana en las mentes humanas o en el sustrato físico de los cerebros humanos?

Por último, ¿cómo se puede implementar eficazmente el aprendizaje y la inferencia con modelos de mundos complejos en mentes con recursos finitos, a menudo bastante limitados? ¿Y cómo surgen, en última instancia, nuestras nociones más profundas del conocimiento abstracto en el desarrollo cognitivo? ¿Están estas conectadas a un cerebro o a la maquinaria de una mente desde el nacimiento, o podrían las formas y contenidos fundamentales del conocimiento abstracto ser aprendidos o construidos, en su totalidad o en parte?

El papel del conocimiento abstracto en las últimas dos décadas, muchos aspectos de la cognición de alto nivel han sido iluminados por las matemáticas de la estadística bayesiana: nuestro sentido de similitud^[90], la representatividad^[91] y la aleatoriedad^[92]; coincidencias como pistas ocultas^[93]; juicios de fuerza causal o apoyo probatorio^[94]; razonamiento diagnóstico y condicional^[95]; y predicciones sobre el futuro de los acontecimientos^[96].

La afirmación de que las mentes humanas aprenden y razonan de acuerdo con los principios bayesianos no implica que puedan implementar cualquier inferencia bayesiana. Solo aquellos cálculos inductivos para los que la mente está diseñada para desempeñarse bien —aquellos en los que la biología ha tenido tiempo y razones para desarrollar mecanismos eficaces y eficientes— pueden entenderse en términos bayesianos.

Además de las habilidades cognitivas generales mencionadas, los análisis bayesianos han arrojado luz sobre muchas capacidades específicas que dependen de un procesamiento rápido, confiable e inconsciente, incluyendo la percepción, el lenguaje, la memoria y los sistemas sensoriomotores. En contraste, en tareas que requieren la manipulación consciente y explícita de probabilidades como cantidades numéricas —una invención cultural reciente que pocas personas llegan a dominar, y solo después de un entrenamiento sofisticado— los juicios tienden a estar sesgados, alejándose de las normas bayesianas.

En esencia, la regla de Bayes es simplemente una herramienta para responder a la pregunta fundamental: ¿cómo guía el conocimiento abstracto el aprendizaje y la inferencia a partir de datos incompletos? El conocimiento abstracto se codifica en un modelo generativo probabilístico, un tipo de modelo mental que describe los procesos causales del mundo que dan lugar a las observaciones del aprendiz, así como las variables latentes no observadas que sustentan la predicción y la acción efectiva.

Los modelos generativos deben ser probabilísticos para manejar la incertidumbre del aprendiz sobre los verdaderos estados de las variables latentes y los procesos causales en funcionamiento. Además, un modelo generativo es abstracto en dos sentidos: no solo describe una situación específica, sino también una clase más amplia de situaciones sobre las que el aprendizaje debería generalizar, y captura, de manera parsimoniosa, la estructura esencial del mundo que provoca las observaciones de los aprendices y hace posible la generalización.

La inferencia bayesiana proporciona un marco racional para actualizar las creencias sobre las variables latentes en modelos generativos dados los datos observados. El conocimiento previo se codifica a través de un espacio restringido de hipótesis H sobre los posibles valores de las variables latentes, es decir, las estructuras del mundo observado. Conocimiento de grano más fino viene en las probabilidades previas P(h) que especifican el grado de creencia del aprendiz en cada hipótesis h antes de (o independientemente de) las observaciones.  La regla de Bayes actualiza estas probabilidades previas a probabilidades posteriores (P(h|d) condiciónales a los datos observados d: 

La probabilidad a posteriori es proporcional al producto de la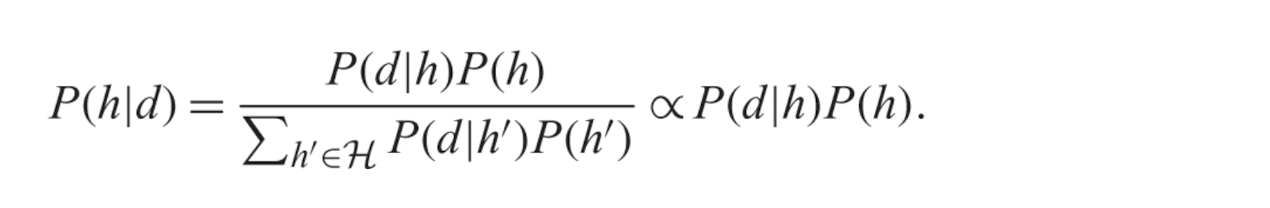 probabilidad previa y la probabilidad (P(h|d), midiendo la probabilidad de los datos bajo la hipótesis h, en relación con todas las demás hipótesis h’ en H. 

Las variables latentes son aquellas que no se pueden observar o medir directamente, pero que se infieren a partir de otras variables observables. Estas variables ocultas son fundamentales en diversos campos, como la psicología, la sociología y la economía, ya que permiten modelar conceptos abstractos o no directamente medibles.

En el contexto de la relatividad general, la causalidad se refiere al principio de que los eventos están conectados de tal manera que un evento puede influir en otro si existe una conexión causal entre ellos. Esto implica que la estructura del espacio-tiempo está organizada de manera que se preserva el orden causal de los eventos, evitando paradojas temporales y asegurando una coherencia lógica en la secuencia de acontecimientos.

La estructura causal del espacio-tiempo se define mediante la métrica, que determina las distancias y los intervalos temporales entre eventos. Esta métrica permite clasificar las separaciones entre eventos en tres categorías:

Tipo tiempo: Eventos que pueden estar conectados causalmente, donde uno puede influir en el otro.

Tipo luz: Eventos separados por la trayectoria de un rayo de luz, representando el límite de la causalidad.

Tipo espacio: Eventos que no pueden influirse mutuamente debido a la separación espacial y la limitación impuesta por la velocidad de la luz.

Esta clasificación es fundamental para entender cómo se relacionan los eventos en el espacio-tiempo y cómo se mantiene la coherencia causal en la teoría de la relatividad general.

Es importante destacar que, aunque el término "tiempo causal" no es una expresión estándar en la literatura de la relatividad general, la comprensión de la causalidad y la estructura temporal es esencial para el estudio de las interacciones y la evolución de los sistemas físicos dentro de este marco teórico.

Para ilustrar la regla de Bayes en acción, supongamos que observamos a Rogelio tosiendo (d) y consideramos tres hipótesis como posibles explicaciones: h1, Rogelio tiene un resfriado; h2, tiene una enfermedad pulmonar; o h3, sufre de acidez estomacal. Intuitivamente, solo h1 parece convincente. La regla de Bayes explica por qué. La probabilidad favorece a h1 y h2 sobre h3: solo los resfriados y las enfermedades pulmonares causan tos y, por lo tanto, elevan la probabilidad de los datos por encima de la línea de base. El prior, en cambio, favorece a h1 y h3 sobre h2: los resfriados y la acidez estomacal son mucho más comunes que las enfermedades pulmonares. La regla de Bayes, y la gama de problemas que puede resolver, sopesa las hipótesis de acuerdo con el producto entre los priors (prioridades) y las probabilidades, y por lo tanto solo produce explicaciones como h1, que puntúan alto en ambos aspectos. Esta es la técnica de la regla de Bayes para resolver.

La inferencia bayesiana se puede utilizar para explicar cómo las personas aprenden a partir de datos dispersos. En el aprendizaje de conceptos, los datos pueden corresponder a varios objetos y las hipótesis a posibles extensiones del concepto. ¿Por qué, dados tres objetos diferentes de una colección de caballos de mar, un niño generalizaría la palabra "caballo" a todos los objetos —y solo a los caballos (h1)? ¿Por qué no h2, todos los caballos excepto los Clydesdales; h3, todos los animales; o cualquier otra regla consistente con los datos? Las probabilidades favorecen los patrones más específicos, h1 y h2; sería una coincidencia muy sospechosa extraer tres ejemplos aleatorios que caigan dentro de los conjuntos más pequeños (h1 o h2) si en realidad se extrajeron del mucho más grande (h3). El prior favorece a h1 y h3, porque como categorías más coherentes y distintivas, es más probable que sean los referentes de palabras comunes en el lenguaje. Solo h1 obtiene una puntuación alta en ambos términos.

Asimismo, en el aprendizaje causal, los datos podrían ser la coocurrencia de eventos, y las hipótesis, posibles relaciones causales que vinculan esos acontecimientos. Las probabilidades favorecen los vínculos causales que hacen que la coocurrencia sea más probable, mientras que los priors favorecen los vínculos que se ajustan a nuestro conocimiento previo sobre qué tipos de eventos es probable que causen a otros. Por ejemplo, es más probable que una enfermedad cause un síntoma (por ejemplo, la tos) que al revés.

Visto en estos términos, la regla de Bayes proporciona un marco cuantitativo simple para responder preguntas sobre la inferencia inductiva. En particular, indica cómo se deben combinar los conocimientos previos con los datos para obtener un programa de investigación que permita ir hacia atrás desde los datos que las personas observan y las conclusiones a las que llegan, hasta el conocimiento que debe haber informado sus inferencias. Este proyecto de caracterizar los sesgos inductivos de las personas, expresados en forma de distribuciones previas, caracterizó gran parte de nuestro trabajo temprano sobre modelos bayesianos de cognición. A lo largo del camino, también desarrollamos sofisticados métodos experimentales para revelar distribuciones previas humanas, basados en algoritmos utilizados en estadística e informática. Por ejemplo, bajo ciertos supuestos, la información que se transmite de persona a persona, como en el juego del teléfono, converge hacia una forma que refleja los sesgos inductivos de las personas involucradas. Estos métodos permiten cuantificar el conocimiento abstracto de las personas a través de una amplia gama de problemas, dándonos los ingredientes para formular generalizaciones sobre su forma y orígenes.

4.14.1 La forma de conocimiento abstracto

El conocimiento abstracto proporciona restricciones esenciales para el aprendizaje, pero ¿en qué forma? Esto nos lleva a la siguiente pregunta, Q2: ¿qué forma adopta nuestro conocimiento del mundo abstracto a través de diferentes dominios y tareas? Para tareas cognitivas complejas, como el aprendizaje de conceptos o el razonamiento causal, es imposible simplemente enumerar todas las hipótesis lógicamente posibles junto con sus antecedentes y probabilidades. Algunas formas más sofisticadas de representación del conocimiento deben subyacer a los modelos generativos probabilísticos de contrafactuales en la cognición bayesiana.

En los enfoques asociativos o conexionistas tradicionales, los modelos estadísticos de aprendizaje se definían sobre grandes vectores numéricos. El aprendizaje se concebía como la estimación de fuerzas en una memoria asociativa, pesos en una red neuronal o parámetros de una función no lineal de alta dimensión^[97]. Los modelos cognitivos bayesianos, por el contrario, han tenido más éxito en la definición de probabilidades que las formas simbólicas más estructuradas de representaciones del conocimiento utilizadas en la informática y la inteligencia artificial, como grafos, gramáticas, lógica de predicados, esquemas racionales y programas funcionales. Se utilizan diferentes formas de representación para capturar el conocimiento de las personas en distintos dominios y tareas, así como en diferentes niveles de abstracción. Al aprender palabras y conceptos a partir de ejemplos, el conocimiento que guía las generalizaciones tanto de niños como de adultos se ha descrito adecuadamente mediante modelos probabilísticos definidos sobre representaciones estructurales en forma de árboles^[98]. El razonamiento sobre otros conceptos biológicos relacionados con los tipos naturales (por ejemplo, dado que las vacas y los rinocerontes tienen la proteína X en sus músculos, ¿qué tan probable es que los caballos o las ardillas también la tengan?) está igualmente bien descrito por los modelos bayesianos, que asumen que los objetos cercanos en el árbol probablemente compartan propiedades. Sin embargo, los árboles no constituyen una representación universal. Las diferencias entre otros tipos de categorías o propiedades se capturan mejor utilizando modelos probabilísticos con distintas formas: espacios bidimensionales (2D) o cuadrículas para razonar sobre propiedades geográficas de las ciudades; órdenes unidimensionales (1D) para razonar sobre valores o habilidades; o redes dirigidas para representar propiedades transmitidas causalmente entre especies (por ejemplo, las enfermedades^[99]).

Kemp, Charles y Tenenbaum, Joshua mostraron cómo la forma de la estructura en un dominio puede describirse utilizando un modelo bayesiano jerárquico definido sobre gramáticas de grafos. En el nivel inferior del mundo hay una matriz de objetos y sus propiedades, o similitudes entre pares de objetos. Cada celda de la matriz representa si se observa una característica determinada (columna) para un objeto específico (fila). Un nivel más arriba, un grafo describe cómo se distribuyen las propiedades entre los objetos. Intuitivamente, se espera que los objetos cercanos en el grafo compartan propiedades. En el nivel más alto, las reglas gramaticales especifican la forma de la estructura en el dominio, es decir, las reglas para hacer crecer el grafo de manera restringida a partir de un nodo semilla inicial.

Un algoritmo de búsqueda intenta encontrar la combinación de una gramática de forma y un grafo generado por esa gramática que, en conjunto, reciba la mayor probabilidad. A) Dadas las observaciones sobre las características de los objetos, el algoritmo infiere que una estructura de árbol explica mejor los datos. El mejor árbol encontrado captura categorías intuitivamente sensatas a múltiples escalas. B) El mismo algoritmo descubre que los patrones de votación de los ciudadanos se explican mejor mediante un aspecto lineal de “izquierda a derecha”. C) Las similitudes subjetivas entre los colores se explican mejor mediante un anillo circular. D) Dadas las proximidades entre ciudades del globo, el algoritmo descubre una representación cilíndrica análoga a la latitud y la longitud: el producto cruzado de un anillo y un anillo. E) Dadas las imágenes de rostros sintetizados de manera realista, que varían en dos dimensiones —raza y masculinidad—, el algoritmo recupera con éxito la estructura de la cuadrícula 2D subyacente: un producto cruzado de dos cadenas^[100].  

¿Qué es una teoría de la mente? ¿Cómo podemos formalizar las diversas teorías de la mente que estudiamos como científicos cognitivos? Argumentamos que es valioso pensar en una teoría de la mente como un tipo de lenguaje de programación: uno especializado en plantear y razonar sobre problemas que involucran otras mentes. Basándonos en ideas de la teoría y la historia de los lenguajes de programación, mostramos cómo esta perspectiva puede ayudarnos a formalizar conceptos en una teoría de la mente, articular con precisión las diferencias entre múltiples teorías de la mente y razonar sobre cómo desarrollamos nuestras teorías de la mente a lo largo del tiempo^[101].

Una característica clave de la teoría de la mente humana es la capacidad de atribuir creencias a otros agentes como explicaciones mentalistas de su comportamiento. Sin embargo, dada la amplia variedad de creencias que los agentes pueden tener sobre el mundo y el rico lenguaje que podemos usar para expresarlas, ¿qué creencias específicas tienden las personas a atribuir a los demás? Se ha investigado la hipótesis de que las personas prefieren atribuir creencias que expliquen adecuadamente el comportamiento que observan. Se desarrolla un modelo computacional que cuantifica la fuerza explicativa de una afirmación (en lenguaje natural) sobre las creencias de un agente mediante tres factores: precisión, informatividad y relevancia causal para las acciones, cada uno de los cuales puede calcularse a partir de un modelo generativo probabilístico de comportamiento impulsado por creencias. Utilizando este modelo, estudiamos el papel de cada factor en cómo las personas atribuyen selectivamente creencias a otros agentes. Investigamos esto mediante un experimento en el que los participantes observan a un agente recolectar llaves escondidas en cajas para alcanzar un objetivo y luego clasifican un conjunto de afirmaciones que describen las creencias del agente sobre el contenido de las cajas. Observamos que la precisión y la informatividad funcionan razonablemente bien para predecir estas clasificaciones cuando se combinan, pero que la relevancia causal es el único factor que mejor explica las respuestas de los participantes^[102].

La capacidad humana de pensar sobre el pensamiento ("teoría de la mente") es un objeto de estudio fundamental en muchas disciplinas. En las últimas décadas, investigadores de estas disciplinas han convergido en un paradigma computacional complejo para modelar la teoría de la mente, basado en el razonamiento probabilístico recursivo. Sin embargo, los profesionales suelen encontrar la programación en este paradigma extremadamente desafiante: primero, porque pensar sobre el pensamiento resulta confuso para los programadores, y segundo, porque los modelos son extremadamente lentos de ejecutar. El “memo”, un nuevo lenguaje de programación probabilística de dominio específico que supera estos desafíos: primero, al proporcionar sintaxis y semántica especializadas para la teoría de la mente, y segundo, al adoptar un enfoque único para la inferencia que escala bien en hardware moderno mediante programación de matrices “memo” permite a los profesionales escribir modelos significativamente más rápidos con mucho menos código, y ya ha sido adoptado por varios propósitos de investigación^[103].

El conocimiento sobre causas y efectos, de manera más general, puede representarse mediante grafos dirigidos: una estructura en la que los nodos representan variables y los bordes dirigidos entre nodos representan vínculos causales probabilísticos. En un entorno médico, por ejemplo, los nodos pueden representar que un paciente tiene un resfriado, tos, fiebre u otra afección, y la presencia o ausencia de bordes muestra que los resfriados tienden a causar tos y fiebre, pero no dolor en el pecho; la enfermedad pulmonar tiende a causar tos y dolor en el pecho, pero no fiebre; y así sucesivamente.

Tal mapa causal representa un tipo simple de teoría intuitiva, pero el aprendizaje de redes causales a partir de datos limitados depende de las limitaciones de un conocimiento más abstracto. Por ejemplo, el aprendizaje de las dependencias causales entre condiciones médicas es posible gracias a una teoría de marco de nivel superior que especifique dos clases de variables (o nodos): enfermedades (D) y síntomas (S), y la tendencia de las relaciones causales (bordes del grafo) a ir de D a S, en lugar de dentro de estas clases, o de S a D. Este marco abstracto puede representarse utilizando modelos probabilísticos definidos sobre estructuras de datos relacionales como esquemas de grafos, plantillas para grafos basadas en tipos de nodos, o gramáticas de grafos de probabilidad, similares en espíritu a las gramáticas probabilísticas para cadenas, que se han convertido en estándar para representar el conocimiento lingüístico.

En el nivel más abstracto, el concepto mismo de causalidad —en el sentido de una relación dirigida que apoya la intervención o manipulación por parte de un agente externo— puede formularse como un conjunto de leyes lógicas que expresan restricciones sobre la estructura de grafos dirigidos que relacionan acciones y eventos observables.

Cada una de estas formas de conocimiento hace que diferentes tipos de distribuciones previstas sean naturales de definir y, por lo tanto, impone diferentes restricciones a la inducción. La generalización exitosa depende de que estas restricciones sean correctas. Si bien las restricciones inductivas a menudo se matizan, es más fácil apreciar los efectos de las restricciones cualitativas que simplemente limitan las hipótesis que los estudiantes pueden considerar (es decir, establecer priores a cero para muchas hipótesis lógicas posibles).

Por ejemplo, en el aprendizaje de conceptos sobre un dominio de n objetos, hay 2ⁿ subconjuntos y, por tanto, 2ⁿ hipótesis lógicamente posibles para la extensión de un concepto novedoso. Suponiendo que los conceptos corresponden a las ramas de un árbol binario específico sobre los objetos, esto restringe el espacio a solo n-1 hipótesis.

Al aprender una red causal sobre 16 variables, hay aproximadamente 10⁴⁶ hipótesis lógicamente posibles (grafos acíclicos dirigidos), pero una teoría marco que restringe las hipótesis a grafos bipartitos de enfermedad-síntoma reduce esto a aproximadamente 10²³ hipótesis. Saber qué variables pertenecen a las clases de enfermedad y síntomas restringe aún más esto a aproximadamente 10¹⁸ redes.

Cuanto más pequeño sea el espacio de hipótesis, con mayor precisión se puede esperar que un estudiante generalice, pero solo mientras la verdadera estructura que se desea aprender permanezca dentro o cerca (en un sentido probabilístico) del espacio de hipótesis del estudiante.

No es coincidencia, entonces, que nuestras mejores explicaciones de las representaciones mentales de las personas a menudo se parezcan a versiones más simples de cómo los científicos representan los mismos dominios, como las estructuras de los árboles para las especies biológicas. Una descripción compacta que se aproxima a cómo funciona realmente el grano fino del mundo ofrece la forma más útil de restricción en el aprendizaje inductivo.

4.14.2 El origen del conocimiento abstracto 

La necesidad de conocimiento abstracto, y la necesidad de hacerlo bien, nos lleva a una pregunta: ¿cómo aprenden los estudiantes lo que necesitan saber para hacer posible el aprendizaje? ¿Cómo sabe un niño qué estructura de árbol es la forma correcta de organizar hipótesis para el aprendizaje de palabras? A un nivel más profundo, ¿cómo puede un estudiante saber que un dominio dado de entidades y conceptos debe representarse usando un árbol, en lugar de un espacio de baja dimensión u otra forma? O, en el aprendizaje causal, ¿cómo se llega a corregir las teorías marco, como el conocimiento abstracto de enfermedades y síntomas, hacia variables con vínculos causales que van de enfermedades a síntomas?

¿Qué es un árbol de probabilidad?

—Un árbol de probabilidad es un diagrama ramificado, donde:

—Cada rama representa un resultado posible de un evento.

—A cada rama se le asigna una probabilidad.

—Las probabilidades se multiplican a lo largo de las ramas para calcular la probabilidad de una secuencia completa de eventos.

Partes del árbol de probabilidad

—Nodo inicial: el punto de partida del experimento.

—Ramas: representan los posibles resultados de cada evento.

—Probabilidades: asociadas a cada rama (deben sumar 1 en cada punto de decisión).

—Nodos intermedios: puntos donde se desarrollan eventos posteriores.

—Hojas o nodos terminales: representan los resultados finales, con su probabilidad total.

En epistemología y filosofía de la ciencia

En contextos filosóficos, una restricción inductiva es una limitación al tipo de inferencias inductivas que se consideran válidas o justificables.

Por ejemplo, podríamos considerar que una teoría científica debe hacer predicciones verificables. Eso sería una restricción inductiva metodológica.

También se relaciona con el problema de la inducción no justificada (como en Hume): necesitamos restricciones para delimitar qué generalizaciones son razonables.

La adquisición de conocimiento abstracto —así como el desarrollo de nuevas restricciones inductivas— es una competencia central del desarrollo cognitivo. Por ejemplo, en las primeras etapas del aprendizaje del lenguaje, los niños tienden a asumir una clasificación plana y mutuamente excluyente de los objetos: cada objeto tiene un solo nombre, y cada nombre se refiere a un único tipo de objeto. Sin embargo, a medida que su capacidad cognitiva se expande, descubren que las categorías no son planas, sino que deben organizarse en jerarquías estructuradas, similares a árboles, donde los conceptos generales engloban subconjuntos más específicos^[104]. Con el tiempo, los niños desarrollan la capacidad de organizar categorías en niveles jerárquicos, como "animal > perro > dálmata. Este cambio implica una nueva restricción inductiva más compleja, en la que entienden que los conceptos no son planos, sino anidados y relacionados por inclusión.

4.15 Razón primera

El punto de vista que argumenta que el sujeto considera factores que empujan la realidad en diferentes direcciones no está simplemente prestando atención a una fuente de evidencia entre otras que tienen que ver con lo que debería hacer; más bien, está adquiriendo el tipo de perspectiva que le ayuda a comprender por qué debería hacerlo así.

De acuerdo con este punto de vista, las razones explican lo que debes hacer no solo en el sentido de lo que importa y debes hacer; la explicación de por qué deberías hacerlo cuenta como una "razón" para que lo hagas. En el sentido de que los hechos sobre cuáles son tus razones y la dirección en la que apuntan son anteriores y explicativos de lo que debes hacer. Algo cuenta como lo que debes hacer en virtud del hecho de que es lo que favorece la balanza de tus razones, y eso es lo que significa que sea lo que debes hacer. Con respecto a la cuestión de lo que se debe hacer, este punto de vista es que las razones tienen —o dicho más cuidadosamente, la relación de razón tiene— prioridad tanto analítica como explicativa.

Según muchos filósofos morales contemporáneos, la prioridad de las razones se extiende no solo a lo que debemos hacer, sino también a muchos o a todos los demás conceptos distintivos de la ética o de la filosofía práctica, como bueno, mejor, admirable, justo, malvado, escandaloso, imbécil, injusto, justificado, correcto y muchos otros. Del mismo modo que lo que deberíamos hacer puede considerarse una cuestión de lo que nuestras razones apoyan mejor, estos filósofos afirman que cada uno de estos otros conceptos necesita ser entendido y explicado en términos de razones. Estos filósofos dan prioridad a las razones sobre una gama mucho más amplia de importantes categorías y conceptos éticos, evaluativos o, más ampliamente, normativos.

Nos interesa la versión más fuerte de la idea de que las razones son explicativamente centrales en la ética. De acuerdo con esta versión, las razones son anteriores y explicativas no solo de lo que debemos hacer, y anteriores y explicativas de muchas propiedades y relaciones éticas o evaluativas, sino anteriores y explicativas de toda propiedad y relación normativa. De acuerdo con esta versión de la tesis, las razones no solo son útiles para formular tesis en términos neutros, y no solo preceden a una gama interesante o importante de otros conceptos, sino que son las primeras simpliciter, al menos entre los conceptos normativos. Entre las propiedades y relaciones normativas, las razones son las más fundamentales. Llamaremos a esto la tesis de las razones primeras.

La palabra "normativo" se ha utilizado muchas veces en filosofía moral para contrastar con "evaluativo", de modo que "normativo" abarca "incorrecto", "debe", "debería" y "justo", pero no "bueno" o "hábil". Así como es importante aclarar lo que comprendemos por "normativo", también es importante aclarar lo que comprendemos por "razón", para precisar la tesis de Razones primeras. Los filósofos distinguen rutinariamente entre muchos tipos diferentes de afirmaciones que se pueden hacer usando la palabra "razón". Tendremos mucho más que decir sobre cómo entenderemos qué son las razones, en el sentido relevante. Por ahora, bastará decir que es un sentido normativo de la "razón" en el que las razones están en primer lugar. No basta con defender las Primeras razones para argumentar que toda propiedad o relación normativa debe entenderse en términos de explicación y, por lo tanto, en términos de respuestas a las preguntas de "por qué", o dicho de otra manera, razones por las que algo es el caso. Semejante punto de vista hace que las llamadas razones "explicativas" sean más fundamentales que cualquier propiedad o relación normativa, pero no equivaldría por sí mismo a la afirmación de que las razones ocupan el primer lugar entre las propiedades y relaciones normativas. Propiedades y relaciones forman la base de cómo entendemos y evaluamos las interacciones humanas en contextos regulados por normas. Propiedades y relaciones: obligatoriedad, permisibilidad, prohibición, derecho, deber y responsabilidad.

La tesis de la Razón primera se encuadra en una familia de tesis prioritarias. En diferentes épocas, los filósofos morales han tenido la costumbre de proclamar que el objeto de la ética es simplemente el objeto del bien, o alternativamente que es simplemente lo que debería ser. Cada una de estas proclamaciones suele venir acompañada de un compromiso con una concepción de cuál propiedad o relación normativa es lo primero. Las razones primeras comparten con cada uno de estos puntos de vista la idea de que alguna propiedad o relación normativa es central, pero ofrece una respuesta distintiva a lo que es.

La epistemología se ocupa de cuestiones tales como en qué circunstancias es racional creer que la universidad estará abierta mañana, y por qué. ¿Y cuándo es razonable estar más seguro de que un neoliberal será elegido que de que lo hará un liberal? La epistemología también hace preguntas sobre cuánta evidencia necesitas antes de tomar una decisión, y si debes tener menos confianza en tus puntos de vista cuando descubres que hay personas igualmente inteligentes que han llegado a conclusiones diferentes sobre la base de la misma evidencia. De modo que la epistemología es, al menos en parte, una disciplina normativa.

Una generación anterior a Descartes, en voz de Montaigne, se preguntó: "¿qué sé yo?" Tampoco Descartes llegó a su empresa con una mente totalmente inocente: él mismo tuvo una intensa educación en la filosofía de la época, de maestros jesuitas. Pero en la época de Descartes las cosas estaban cambiando. El astrónomo polaco Copérnico había descubierto el modelo heliocéntrico del sistema solar. Galileo y otros estaban sentando las bases de una ciencia “mecánica” de la naturaleza. En esta imagen, las únicas sustancias en el espacio serían materiales, formadas por “átomos”, y causadas por el movimiento solo por fuerzas mecánicas que la ciencia descubriría con el tiempo. Tanto Copérnico como Galileo cayeron en desgracia con los guardianes de la ortodoxia católica, la Inquisición, ya que esta imagen científica parecía a muchas personas amenazar el lugar de los seres humanos en el cosmos. Si la ciencia nos dice todo lo que hay, ¿qué pasa con el alma humana, la libertad humana y nuestra relación con Dios?

Descartes fue muy inteligente, inventó la notación algebraica estándar; y las coordenadas cartesianas, que nos permiten dar ecuaciones algebraicas para figuras geométricas, llevan su nombre. Él mismo fue uno de los líderes de la revolución científica, haciendo avances fundamentales no solo en matemáticas, sino también en física, particularmente en óptica. Pero Descartes también era un católico piadoso. Por lo tanto, su tarea de gran importancia fue mostrar cómo el mundo científico que se desarrollaba, vasto, frío, matemático y mecánico, tenía, sin embargo, espacio para Dios y la libertad de pensamiento. De ahí la obra de su vida, que culminó en las Meditaciones (1641), en la que intentó demostrar la existencia de Dios y la distinción entre mente humana y cuerpo. Pero el subtexto es que Descartes también tenía la intención de rescatar la visión moderna del mundo de la acusación de ateísmo y materialismo. El mundo científico iba a ser menos amenazante de lo que se temía. Debía ser seguro para los seres humanos. Y la forma de hacerlo seguro era reflexionar sobre los fundamentos del conocimiento. Así que comenzamos con Descartes porque fue el primer gran filósofo que luchó con las implicaciones de la visión moderna del mundo.

Hay seis Meditaciones. En la primera, Descartes introduce el “método de la duda”. Resuelve que si ha de establecer algo en las ciencias que sea “estable y que pueda perdurar”, debe demoler todas sus opiniones ordinarias y comenzar desde los cimientos.

Porque ha descubierto que incluso sus sentidos lo engañan, y es “prudente no confiar nunca completamente en aquellos que nos han engañado ni una sola vez”. Se plantea Descartes a sí mismo la objeción de que solo los locos “que dicen que están vestidos de purpura cuando en realidad están desnudos”; los locos son evidentemente bastante coloridos en el siglo XVII, niegan la evidencia muy obvia de sus sentidos. En respuesta a esto, nos recuerda los sueños, en los que podemos representar cosas a nosotros mismos de manera tan convincente como lo hacen ahora nuestros sentidos, pero que no tienen ninguna relación con la realidad. Aun así, se opone a sí mismo, los sueños son como pinturas. Un pintor puede reorganizar las escenas, pero en última instancia representa cosas revividas de cosas “reales”, aunque solo sean colores reales. Por un razonamiento similar, dice Descartes, incluso si las cosas familiares son imaginarias, deben depender de alguna cosa más simple y universal en el fondo de lo real. Pero, ¿qué cosas? Descartes pensó que “no hay una sola de nuestras creencias anteriores sobre la que no pueda plantearse una duda”. Y en esta etapa: “supongo que no es Dios, que es supremamente bueno y la fuente de la verdad, sino más bien algún demonio malicioso del mayor poder y astucia que ha empleado todas sus energías para engañarme. Pensaré que el cielo, el aire, la tierra, los colores, las formas, los sonidos y todo lo externo son más que las ilusiones de los sueños que él ha ideado para atrapar mi juicio”.

Este es el demonio maligno de Descartes. Una vez que se plantea esta aterradora posibilidad, su única defensa es resueltamente guardarse de creer cualquier cosa. Reconoce que esto es difícil de hacer, y una especie de pereza lo devuelve a la vida normal, pero intelectualmente, su único camino es trabajar en la “oscuridad inextricable” de los problemas que ha planteado a la realidad. Con esto termina la primera Meditación de Descartes.

Referencias

[1] Noam Chomsky (2004) Chomsky on Mis-Education.  Rowman & Littlefield Publishers

[2] John-Ashbery (1977 ) Self-portrait-in-a-convex-mirror. Penguin Poets

[3] Horsten, Leon. (2011). The Tarskian Turn: Deflationism and Axiomatic Truth. 10.7551/mitpress/9780262015868.001.0001.

[4] Garner, Roberta. (2012). Plastic Fantastic: How the Biggest Fraud in Physics Shook the Scientific World by Eugenie Samuel Reich. Science & Society. 76. 117-119. 10.2307/41510530.

[5] Parker, W. S. (2013). Ensemble Modeling, Uncertainty and Robust Predictions. Wiley Interdisciplinary Reviews: Climate Change, 4(3), 213-223.

[6] Brzović, Z., Balorda, V., & Šustar, P. (2021). Explanatory Hierarchy of Causal Structures in Molecular Biology. European Journal for Philosophy of Science, 11(2), 1-21.

[7] ratt, S. L. (2021). Decolonizing “Natural Logic”. In J. Brumberg-Chaumont & C. Rosental (Eds.), Logical Skills: Social-Historical Perspectives (pp. 23-50). Cham: Springer Verlag.

[8] Paul, E. S. (2024). The rational force of clarity: Descartes’s rejection of psychologism. Res Philosophica, 101(3), 431-457.

[9] Eklund, M. (2020). “Making Sense of Logical Pluralism.” Inquiry, 62(3-4), 433-454

[10] Dalrymple, M., & Findlay, J. Y. (2019). “Lexical Functional Grammar”. En A. Kertész, E. Moravcsik & C. Rákosi (Eds.), Current Approaches to Syntax: A Comparative Handbook (pp. 123-154). Berlin: De Gruyter Mouton.

[11] Turri, J. (2010). “Contingent a priori knowledge.” Philosophy and Phenomenological Research, 83(2), 327-344.

[12] Baras, D. (2017). “Our Reliability Is in Principle Explainable.” Episteme, 14(2), 197-211.

[13] Roland, J. W. (2007). “Maddy and Mathematics: Naturalism or Not.” British Journal for the Philosophy of Science, 58, 423-450

[14] Boghossian, P. A. (2019). “Inference, Agency, and Responsibility.” En M. Balcerak-Jackson & B. Balcerak-Jackson (Eds.), Reasoning: New Essays on Theoretical and Practical Thinking (pp. 101-124). Oxford: Oxford University Press.

[15] Knauff, M., Mulack, T., Kassubek, J., Salih, H. R., & Greenlee, M. W. (2002). Spatial imagery in deductive reasoning: A functional MRI study. Brain Research: Cognitive Brain Research, 13(2), 203-212.

[16] Martin, B., & Hjortland, O. T. (2021). Logical Predictivism. Journal of Philosophical Logic, 50, 285-318.

[17] Soler, L., Zwart, S., Lynch, M., & Israel-Jost, V. (2014). Introduction. In L. Soler, S. Zwart, M. Lynch & V. Israel-Jost (Eds.), Science after the Practice Turn in the Philosophy, History, and Social Studies of Science (pp. 1–43). London: Routledge.

[18] Shapiro, S. (2000). “Mathematics and Its Philosophy.” En Mathematics and Its Philosophy: Interpreting the Likeness of Things (pp. 21-35). Oxford: Oxford University Press.

[19] Rittberg, C. J. (2019). “On the Contemporary Practice of Philosophy of Mathematics.” Acta Baltica Historiae et Philosophiae Scientiarum, 7(1)

[20] Tanswell, F. S. (2018). “Conceptual Engineering for Mathematical Concepts.” Inquiry: An Interdisciplinary Journal of Philosophy, 61(8), 881-913

[21] Grosholz, E. R. (2007). Representation and productive ambiguity in mathematics and the sciences. Oxford: Oxford University Press.

[22] Winsberg, E. (2001). “Simulations, models and theories: Complex physical systems and their representation.” Philosophy of Science, 68(Supplement), S442–S454.

[23] Avigad, J. (2022). “Varieties of mathematical understanding.” Bulletin of the American Mathematical Society, 59(1), 99-117.

[24] Hamami, Y., & Morris, R. L. (2020). “Philosophy of mathematical practice: A primer for mathematics educators.” ZDM: The International Journal on Mathematics Education, 52(6), 1113-1126.

[25] Beall, J. C., & Restall, G. (2000). “Logical Pluralism.” Australasian Journal of Philosophy, 78(4), 475–493. https://doi.org/10.1080/00048400012349751

[26] Russell, G. (2008). “One true logic?” Journal of Philosophical Logic, 37(6), 593–611. https://doi.org/10.1007/s10992-008-9093-3

[27] Steinberger, F. (2019). The Normative Status of Logic. Oxford: Oxford University Press.

[28] Cook, R. T. (2010). “Let a thousand flowers bloom: A tour of logical pluralism.” Philosophy Compass, 5(6), 492–504. https://doi.org/10.1111/j.1747-9991.2010.00303.x

[29] Priest, G., Beall, J. C., & Armour-Garb, B. (Eds.). (2004). The Law of Non-Contradiction: New Philosophical Essays. Oxford: Oxford University Press.

[30] Tarski, A. (1944). The semantic conception of truth and the foundations of semantics. Philosophy and Phenomenological Research, 4(3), 341–375. https://doi.org/10.2307/2102968

[31] Caret, C. R. (2021). Why Logical Pluralism? Synthese, 198(5), 4947-4968.

[32] Houkes, W., & Zwart, S. D. (2019). Transfer and templates in scientific modelling. Studies in History and Philosophy of Science Part A, 77, 93-100. https://doi.org/10.1016/j.shpsa.2017.11.003

[33] Lin, C.-H. (2022). Knowledge transfer, templates, and the spillovers. European Journal for Philosophy of Science, 12(1), 1-30. https://doi.org/10.1007/s13194-022-00502-8

[34] Nosonovsky, M. (2017). Logical and information aspects in surface science: Friction, capillarity, and superhydrophobicity. arXiv preprint. https://arxiv.org/abs/1712.06589

[35] Quine, W. V. O. (1995). From Stimulus to Science. Cambridge, MA: Harvard University Press.

[36] Field, H. (2009). What is the normative role of logic? Aristotelian Society Supplementary Volume, 83(1), 251-268.

[37] Priest, G. (2008). An Introduction to Non-Classical Logic: From If to Is (2nd ed.). Cambridge: Cambridge University Press.

[38] Martin, B., & Hjortland, O. T. (2021). Logical predictivism. Journal of Philosophical Logic, 50, 285-318.

[39] Frege, G. (1891). “Function and Concept”. In J. van Heijenoort (Ed.), From Frege to Gödel: A Sourcebook in Mathematical Logic 1879-1931. Cambridge, MA : Harvard University Press.

[40] Woods, J. (2020). Against reflective equilibrium for logical theorizing. Australasian Journal of Logic, 17(1), Article 4.

[41] BonJour, L. (2000). Four Theses Concerning A Priori Justification. In Proceedings of the Twentieth World Congress of Philosophy, 5, 13-20.

[42] Chudnoff, E. (2013). Intuition. New York: Oxford University Press.

[43] Ayer, A. J. (1968). The Origins of Pragmatism. London: Macmillan.

[44] Richardson, A. W. (1998). Carnap’s Construction of the World: The Aufbau and the Emergence of Logical Empiricism. Cambridge: Cambridge University Press.

[45] Katz, J. J. (2004). Sense, Reference, and Philosophy. Oxford: Oxford University Press.

[46] Boghossian, P. A. (2008). Content and Justification: Philosophical Papers. Oxford: Oxford University Press.

[47] Burgess, J. P. (2005). No Requirement of Relevance. In S. Shapiro (Ed.), The Oxford Handbook of Philosophy of Mathematics and Logic (pp. 727‑750). Oxford: Oxford University Press.

[48] Littman, G., & Simmons, K. (2004). A Critique of Dialetheism. In G. Priest, J. C. Beall, & B. Armour‑Garb (Eds.), The Law of Non‑Contradiction: New Philosophical Essays (pp. 1–226). Oxford: Oxford University Press.

[49] Rodrigues, A. (2025). What is this thing called Dialetheism? Principia, 29(2), 181–201.

[50] Anderson, S. R. (1992). A Notional Theory of Grammar. London: Routledge.

[51] Baker, M. C. (1997). Thematic Roles and Syntactic Structure. Cambridge: Cambridge University Press.

[52] Priest, G. (2008). An Introduction to Non‑Classical Logic: From If to Is. Cambridge: Cambridge University Press.

[53] Lo Guercio, N., & Rubin, M. (2024). Revisiting McGee’s counterexample to modus ponens. European Journal of Analytic Philosophy, 20(2), 389‑412.

[54] Piller, C. (1996). Vann McGee’s counterexample to modus ponens. Philosophical Studies, 82(1), 27‑54.

[55] Weber, Z. (2022). “Paraconsistent logics find structure in our inconsistent world”. Aeon Essays. Retrieved from https://aeon.co/essays/paraconsistent-logics-find-structure-in-the-noisy-world

[56] Lowe, E. J. (2002). A survey of metaphysics. Oxford: Oxford University Press.

[57] Van Inwagen, P. (2022). Being: A Study in Ontology. Oxford University Press.

[58] Hawking, S. W., & Mlodinow, L. (2010). The grand design. Bantam Books.

[59] Le Poidevin, R. (2009). Incarnation: Metaphysical issues. Philosophy Compass, 4(4), 703–714. https://doi.org/10.1111/j.1747-9991.2009.00222.x

[60] Bennett, K. (2017). Making Things Up. Oxford University Press.

[61] Van Inwagen, P. (1990). Material Beings. Ithaca, NY: Cornell University Press.

[62] Unger, P. K. (1979). Why there are no people. Midwest Studies in Philosophy, 4(1), 177–222.

[63] Lewis, D. K. (1986). On the plurality of worlds. Oxford / Blackwell

[64] Frances, B. (2015.). Worrisome Scepticism about Philosophy. Conferencia de la Dutch–Flemish Association for Analytic Philosophy (VAF), Erasmus University Rotterdam, Rotterdam, País Bajos.

[65] Nozick, R. (2001). Invariances: The structure of the objective world. Cambridge, MA: The Belknap Press of Harvard University Press.

[66] Bennett, K. (2009). Composition, colocation, and metaontology. In D. Chalmers, D. Manley, & R. Wasserman (Eds.), Metametaphysics: New essays on the foundations of ontology (pp. 38-76). Oxford, UK: Oxford University Press.

[67] Machery, E. (2017). Philosophy within its proper bounds. Oxford, UK: Oxford University Press.

[68] Sider, T. (2011). Writing the Book of the World. Oxford University Press.

[69] Cameron, R. P. (2021). Truthmaking and metametaphysics. In R. Bliss & J. T. M. Miller (Eds.), The Routledge handbook of metametaphysics (pp. 233-244). London, UK: Routledge.

[70] Paul, L. A. (2012). Building the world from its fundamental constituents. Philosophical Studies, 158(2), 221-256.

[71] Lewis, D. K. (1986). Philosophical Papers, Volume II. New York, NY: Oxford University Press.

[72] Paul, L. A. (2012). Metaphysics as modeling: The handmaiden’s tale. Philosophical Studies, 160(1), 1-29. https://doi.org/10.1007/s11098-012-9910-x

[73] Melissa Burch (2025) The Criminal Record Complex: Risk, Race, and the Struggle for Work in America. Princeton University Press

[74] Bricker, P. (2020). Modal Matters: Essays in Metaphysics. Oxford, UK: Oxford University Press.

[75] Huemer, M. (2009). A paradox for weak deontology. Utilitas, 21(4), 464-477.

[76] Shalkowski, S. A. (2010). IBE, GMR, and metaphysical projects. In B. Hale & A. Hoffman (Eds.), Modality: Metaphysics, Logic, and Epistemology (pp. 169-187). Oxford, UK: Oxford University Press.

[77] Saatsi, J. (2017). Realism and the limits of explanatory reasoning. En The Routledge Handbook of Scientific Realism (pp. 200-211). Nueva York, NY: Routledge.

[78] Markus Gabriel (2015) Field o f sense: a new realist ontology. Edinburgh University Press.

[79] Wille, Matthias. (2020). Moderne Logik: Gottlob Frege. 10.1007/978-3-476-04638-3_21.

[80] Legg, Leopold. (2010). Matthew Prior: A Study of his Public Career and Correspondence. 10.1017/CBO9780511710780.

[81] Eli de Gortari (1963) la ciencia en la historia de México. FCE.

[82] Wang, Felix & Trueswell, John. (2022). Being suspicious of suspicious coincidences: The case of learning subordinate word meanings. Cognition. 224. 105028. 10.1016/j.cognition.2022.105028.

[83] Leahy, Brian & Carey, Susan. (2019). The Acquisition of Modal Concepts. Trends in Cognitive Sciences. 24. 10.1016/j.tics.2019.11.004.

[84] Feiman, Roman & Mody, Shilpa & Carey, Susan. (2022). The development of reasoning by exclusion in infancy. Cognitive Psychology. 135. 101473. 10.1016/j.cogpsych.2022.101473.

[85] Turner, Stephen & Nichols, Lawrence. (2024). Conceptual Scheming: L. J. Henderson, Practice, and the Harvard View of Science. Critical Inquiry. 51. 30-49. 10.1086/731708.

[86] Mill, J. S. (1843). A system of logic, ratiocinative and inductive: Being a connected view of the principles of evidence, and methods of scientific investigation. J. W. Parker.

[87] Godfrey-Smith, P. (2003). Theory and reality. University of Chicago Press.

[88] Jason, Gary & Jason, Gary & Jason, G.. (1988). The Logic of Scientific Discovery. Peter Lang Publishers (American University Series)ISBN: 0-8204-0569-8

[89] McAllester, David & Akinbiyi, Takintayo. (2013). PAC-Bayesian theory. Empirical inference. 95-103. 10.1007/978-3-642-41136-6_10. ).

[90] Griffiths, Joshua & Generalization, Thomas. (2000). Generalization, Similarity, and Bayesian Inference. The Behavioral and brain sciences. 24. 10.1017/S0140525X01000061.

[91] Tenenbaum, J. B., & Griffiths, T. L. (2001). Generalization, similarity, and Bayesian inference. Behavioral and Brain Sciences, 24, 629–641.

[92] Griffiths, Thomas & Daniels, Dylan & Austerweil, Joseph & Tenenbaum, Joshua. (2018). Subjective randomness as statistical inference. Cognitive psychology. 103. 85-109. 10.1016/j.cogpsych.2018.02.003.

[93] Con, Cognitive. (2014). Proceedings of the Fourteenth Annual Conference of the Cognitive Science Society. 10.4324/9781315806792.

[94] Lu, Hongjing & Yuille, Alan & Liljeholm, Mimi & Cheng, Patricia & Holyoak, Keith. (2008). Bayesian Generic Priors for Causal Learning. Psychological review. 115. 955-84. 10.1037/a0013256.

[95] Judgment Under Uncertainty. Journal of experimental psychology. General. 136. 430-50. 10.1037/0096-3445.136.3.430.

[96] Rojewski, Alex & Schweiger, Maxwell & Sgouralis, Ioannis & Comstock, Matthew & Pressé, Steve. (2023). An accurate probabilistic step finder for time-series analysis. bioRxiv : the preprint server for biology. 10.1101/2023.09.19.558535. 

Griffiths, Tom & Ghahramani, Zoubin. (2005). Infinite Latent Feature Models and the Indian Buffet Process. Advances in Neural Information Processing Systems. 18.

[97] Rogers, Timothy & Mcclelland, James. (2008). Précis of Semantic Cognition: A Parallel Distributed Processing Approach. The Behavioral and brain sciences. 31. 689-714; discussion 714. 10.1017/S0140525X0800589X.

[98] Lewis, Molly & Frank, Michael. (2016). Understanding the effect of social context on learning: A replication of Xu and Tenenbaum (2007b). Journal of Experimental Psychology: General. 145. e72-e80. 10.1037/xge0000203.

[99] Kemp, Charles & Tenenbaum, Joshua. (2009). "Structured statistical models of inductive reasoning": Correction.. Psychological review. 116. 461. 10.1037/a0015514.

[100] Ullman, Tomer & Stuhlmüller, Andreas & Goodman, Noah & Tenenbaum, Joshua. (2018). Learning physical parameters from dynamic scenes. Cognitive psychology. 104. 57-82. 10.1016/j.cogpsych.2017.05.006.

[101] Chandra, Kartik & Ragan-Kelley, Jonathan & Tenenbaum, Joshua. (2025). Theories of Mind as Languages of Thought for Thought about Thought. 10.31234/osf.io/qhc6y_v1.

[102] Ying, Lance & Hillel, Almog & Truong, Ryan & Mansinghka, Vikash & Tenenbaum, Joshua & Zhi-Xuan, Tan. (2025). Belief Attribution as Mental Explanation: The Role of Accuracy, Informativity, and Causality. 10.48550/arXiv.2505.19376.

[103] Chandra, Kartik & Chen, Tony & Tenenbaum, Joshua & Ragan-Kelley, Jonathan. (2025). A Domain-Specific Probabilistic Programming Language for Reasoning About Reasoning (or: a memo on memo). 10.31234/osf.io/pt863_v2.

[104] Markman, Ellen. (1991). Categorization and naming in children: Problems of induction. Ellen Markman. SERBIULA (sistema Librum 2.0). 12. 10.1017/S0142716400009310.