Primer semestre: Pensamiento aritmético
Unidad Uno: Aplica conceptos básicos de lógica matemática
Unidad Uno: Aplica conceptos básicos de lógica matemática en situaciones de su contexto para desarrollar esquemas de razonamiento estructurado
1.0 Conceptualización de la lógica matemática
La lógica involucra hacer algo más simple. Olvidar los detalles es el proceso de abstracción: encontrar la esencia de una situación y concentrarnos en ella por un tiempo. Es importante destacar que no debemos olvidar los detalles críticos: eso sería simplista en lugar de esclarecedor. Y solo lo hacemos temporalmente; no pretendemos haberlo entendido todo, sino más bien un núcleo central en el que puede enraizarse toda comprensión posterior.
Todos tenemos la necesidad de las verdades del mundo. Para tener éxito, para sobrevivir, para colaborar con otros, necesitamos diferentes formas de determinar qué es la verdad y de convencer a las personas de que tenemos razón. Cualquiera puede hacer afirmaciones sobre lo que cree que es verdad, pero, a menos que las respalde de alguna manera, quizá nadie las crea, y con razón. Por eso existen distintas maneras de acceder a la verdad. La verdad científica se determina mediante el método científico, que es un marco claramente definido para decidir qué tan probable es que algo sea plausible. Por lo general, implica formular una teoría (explicación y predicción), recopilar evidencia y ponerla a prueba rigurosamente contra la experiencia.
A la verdad matemática se accede mediante las lógicas: deductiva, inductiva y abductiva. Todavía podemos usar las emociones para sentirla, comprenderla y convencernos de ella, pero solo la lógica puede verificarla. Esta distinción es importante y sutil. En cierto modo, accedemos a la verdad matemática a través de las emociones, pero no cuenta como verdadera hasta que la hemos verificado mediante la lógica. Las emociones son la energía que nos impulsa en la búsqueda de la verdad.
La palabra “lógica” a veces se usa en desacuerdos para intentar dar peso a un argumento: “lógicamente esto tiene que ser cierto”, “lógicamente eso no puede ser correcto”, o “simplemente no estás siendo lógico”. La palabra “matemáticamente” también se utiliza de este modo. Desafortunadamente, estos usos a menudo no tienen sentido: son más bien un recurso desesperado para apuntalar un argumento débil. Si bien el abuso de estas palabras las devalúa y entristece, soy optimista: elijo encontrar algo alentador en ello. Me anima pensar que, en algún nivel, la gente reconoce que la lógica y las matemáticas son irrefutables y que, por lo tanto, deberían ser capaces de concluir una discusión. Si sus nombres se toman en vano para vencer las ideas de un oponente, al menos esto significa que se reconoce su poder. En lugar de lamentar el malentendido de la lógica y de las matemáticas, prefiero abordarlo con la esperanza de que su fuerza pueda usarse para un buen propósito.
La lógica no es enemiga de la emoción, sino su compañera en la búsqueda por comprender el mundo. La emoción nos impulsa a preguntar; la lógica, a verificar. Ese equilibrio entre la energía vital y el rigor intelectual sostiene la cultura del pensamiento. El abuso cotidiano de expresiones como “lógicamente” o “matemáticamente” revela —aunque sea de modo torpe— que incluso en el lenguaje común reconocemos la autoridad de estas disciplinas. La tarea no es lamentar esa confusión, sino canalizarla: cultivar un uso más consciente de la lógica para que siga siendo un puente hacia la claridad y no un disfraz de certezas falsas y sesgos.
Una de las principales razones para establecer un marco claro de acceso a la verdad es alcanzar acuerdos: sobre las leyes de la naturaleza, las leyes sociales, la paz entre los hombres, la democracia de las ideas. Esto suena radical en un mundo donde la gente parece deleitarse en disentir tanto como sea posible. Incluso sucede en el deporte: el fanatismo se indigna ante decisiones arbitrales que simplemente aplican reglas previamente acordadas. Ese marco claro para llegar a consensos se parece al método clínico. La medicina busca listas de verificación que hagan inequívoco un diagnóstico y que permitan que diferentes profesionales lleguen, de manera consistente, a la misma conclusión.
La lógica persigue lo mismo: reglas claras para que distintas personas puedan inferir conclusiones inequívocas y consistentes. Esto es maravilloso en teoría, y aquí “en teoría” significa en el mundo abstracto de las matemáticas. Las matemáticas poseen una capacidad notable de construir consensos. Como señala Michael Dummett en The Philosophy of Mathematics, la matemática avanza constantemente, mientras que la filosofía parece tambalearse en un desconcierto interminable frente a los mismos problemas iniciales.
¿Por qué los matemáticos logran acuerdos sobre lo verdadero? ¿Por qué esas verdades permanecen válidas miles de años después, mientras otras disciplinas se ven obligadas a revisar sin cesar sus teorías? La respuesta parece residir en la solidez de la lógica. Esa es su gran ventaja: permitir consensos sobre lo plausible y lo verdadero, sobre el error y el sesgo, sobre lo demostrable y lo justificable, sobre la inferencia y la implicación.
Desafortunadamente, muchas personas pretenden ganar una discusión a gritos, porque desconfían del mundo lógico. No aceptan la verdad como un modo de vida. Les resulta irritante tener que verificar sus creencias, levantan muros contra la evidencia, los datos y las regularidades que gobiernan nuestras tecnologías. Así reducen sus voces a lo insustancial, y su intelecto lógico se consume en la pereza cognitiva.
Otra desventaja del mundo lógico es que te obliga a tener los pies en la tierra, porque el mundo de la razón ajusta nuestras hipótesis sobre lo real. Bayes lo expresó como un ajuste matemático de nuestros prejuicios a los datos. Se siente como si regresaras de nuevo al mundo para desenredar las ideas, volver a tierra con creencias sólidas (proposiciones respaldadas por evidencia) y usar poderosas técnicas lógicas —deductivas, inductivas y abductivas— para comprender lo urgente sobre el estado de la sociedad y lo natural. Este es el objetivo: reconocer que todo lo que existe no viola las leyes de la naturaleza, pero todo lo sintético (contrafactual) puede existir, dado que las leyes de la naturaleza no agotan todo lo que puede existir desde su combinación infinita.
1.1 En la ciencia hay que saber apreciar el recorrido y no solo llegar a las respuestas[1]
¿Por qué hay que convencer a un estudiante de ciencias de que se interese por las formas de generar conocimiento en la ciencia? Me ha llevado mucho tiempo aprender algo que debería haber sabido desde hace años: que los puntos de vista que uno favorece —aquellos desde los cuales se genera el lenguaje sobre la realidad física—, aunque ya no estén de moda en su mayor parte, son antiguos y cuentan con poderosos partidarios entre los intelectuales modernos.
Creo haberlo aprendido lo suficientemente bien, y dudo que tenga algo muy nuevo que añadir. Afortunadamente, existen varias razones por las que uno debe seguir preocupándose por la originalidad del pensamiento. Si algo verdaderamente importante es correcto en el pensamiento fundamental, es muy poco probable que alguien no lo haya comprendido antes, de una forma u otra, sin importar las revoluciones que haya atravesado la ciencia.
Tales era un monista de la sustancia. Heráclito, un pensador del proceso. A Popper le fascinaba la falsabilidad como propiedad esencial del conocimiento científico. Richard Rorty sostiene que la ciencia no descubre verdades absolutas sobre una realidad objetiva, sino que es una práctica humana que produce descripciones útiles —teorías y datos— para resolver problemas específicos[2]). La originalidad, en cualquier caso, es lo más fácil del mundo; lo difícil es crear un conocimiento verdadero e interesante. Podemos pensar la originalidad de otra manera: como el resultado de alcanzar un buen pensamiento a partir de nuestro propio debate interno, en lugar de tener un pensamiento que nadie haya tenido antes. En ese sentido, hay una buena dosis de originalidad en la actitud de ese estudiante de ciencias.
Imaginemos que un estudiante no desea aprender a pensar en las formas normativas del conocimiento científico, y cursa actualmente la asignatura de Física, en particular el electromagnetismo de Maxwell, que impacta directamente en la instrumentación de laboratorio y el diseño experimental bioquímico. La disposición mental que asume no es nueva en este campo: usa palabras antiguas, matemáticas de hace 300 años. El punto objetivo de pensar no es simplemente afirmar una verdad sin justificación, como haría un loro verde que repite sin comprender. Por eso, la academia se interesa en contribuir al dictum del estudiante que considera irrelevante aprender a razonar como científico, sin asumir esta tarea como parte esencial de su formación esencial[3].
La ciencia del conocimiento tiene una larga historia, pero parece estar sostenida hoy por una burocracia universitaria sin sentido, que impide que se implemente en el aula. Aunque el tema central no cambia, el lenguaje científico se transforma constantemente (como lo sugiere la revolución científica de Kuhn). Lo que un estudiante es capaz de desarrollar en cada época es un estilo personal de pensamiento científico, esencial para su futuro desempeño profesional y cívico[4].
Una consecuencia de esto es que muchos de los mejores trabajos científicos de hoy en día se están llevando a cabo en el contexto de una revolución del pensamiento. Ciertamente, hacer ciencia sin un buen conocimiento de al menos una parte de la historia es como ser un pintor que pinta sin ningún conocimiento de la historia de la pintura. Es perfectamente posible, e incluso puede salir bien, pero está destinado a empobrecer la práctica de uno (por no hablar del placer al que uno renuncia).
Hemos descubierto que algunas personas tratan el material histórico con algo parecido al desdén. Lo lamentamos profundamente, y nos duele aún más constatar que los científicos parecen estar cada vez más aislados en sus especialidades. Daniel Dennett opina que “todos los científicos… deberían estudiar concienzudamente la historia de la ciencia[5]”. Pero la razón principal que suele darse para estudiar la historia de la ciencia es insuficiente: se dice que la historia de la ciencia es, en gran medida, la historia de errores muy tentadores cometidos por personas muy inteligentes, y que, si no conoces esa historia, es casi seguro que cometerás los mismos errores. Esto es cierto, pero insuficiente. Porque la historia de quienes han hecho bien las cosas muestra que comprendían profundamente realidades que hoy se han perdido. No se trata solo de evitar errores, sino de recuperar formas de pensamiento que ya no sabemos tener. En verdad, como dice Schopenhauer con tristeza: al conocimiento solo se le concede una breve celebración de victoria entre dos largos periodos en los que es condenado como paradójico o menospreciado como trivial[6].
Citemos a Goethe, quien es aún más descorazonador: así como el agua que ha sido desplazada por un barco vuelve a cerrarse inmediatamente detrás de él, del mismo modo, cuando las grandes mentes han dejado a un lado los errores y se han hecho espacio para sí mismas, esos errores se cierran naturalmente muy rápidamente detrás de ellas.
Exagera, quizá, pero hay algo de verdad en esto, especialmente en el caso de la ciencia; o, mejor dicho, porque la ciencia es especialmente vulnerable a los efectos de la moda. En cuanto al pasado, nos sentimos cada vez más atraídos por la ciencia de principios del siglo XX, donde con frecuencia encontramos expresiones de puntos de vista cercanos a los que hoy favorecemos.
¿Debemos entonces renunciar a tratar de persuadir a cualquier estudiante de ciencias de cualquier cosa? Eso implicaría simplemente decir lo que creemos que es verdad, y su fundamento: la evidencia. Sin embargo, esto tiende a ser completamente contraproducente si se intenta persuadir a personas que no están abiertas al cuestionamiento. Solo se logra que se aferren aún más a sus posiciones actuales.
Compruébalo: nunca hemos sido capaces de ser socráticos, de guiar a las personas hacia puntos de vista que inicialmente se inclinan a rechazar. Incluso los intentos más suaves de persuasión casi nunca funcionan. Thomas Hobbes lo señaló con crudeza: “los argumentos rara vez funcionan con los hombres cuando una vez se han comprometido con una opinión contraria”. Si no hay una actitud de escepticismo moderado, no hay manera de mostrarles las causas de sus errores. La persuasión no es cuestión de fuerza, sino de apertura. Sin duda, la verdad debe decirse, pero sin disposición al diálogo, incluso la razón más sólida se estrellará contra el muro de la convicción cerrada.
Una vez que la mente humana ha favorecido ciertos puntos de vista —ya sea porque son generalmente aceptados o porque los encuentra de moda— tiende a reorganizar todo lo demás para confirmar y reforzar esas creencias. Y en caso de que se vea superada por consideraciones más poderosas —argumentos o evidencias— reacciona agresivamente, rechazando esas ideas para asegurarse, entre risas burlonas, de que su autoridad dogmática permanece intacta en su postura inflexible.
Tolstoi estuvo de acuerdo: la mayoría de la gente… muy rara vez pueden discernir incluso la verdad más simple y obvia si es tal que los obliga a admitir la falsedad de las conclusiones que han formado, tal vez con mucha dificultad, conclusiones de las que están orgullosos, que han enseñado a otros y sobre las que han construido sus vidas.
Herbert Feigl adoptó una perspectiva casi psicoanalítica: un rompecabezas que no puede resolverse dentro de un marco de información favorecido tiende a reprimirse del mismo modo en que se reprimen los conflictos intrapersonales no resueltos. Feigl sugiere que, psicológicamente, este tipo de represión cognitiva podría subsumirse bajo los mismos mecanismos que rigen la represión emocional. Algunos eruditos se aferran con tanta fuerza a ciertas ideas, y su perspectiva se vuelve tan autorreferencial, que erigen elaboradas barricadas defensivas simplemente para proteger sus ideas favoritas de los golpes directos o de los efectos corrosivos —más lentos pero constantes— de la crítica.
Aristóteles ya conocía el fenómeno de quien “mantiene una tesis a toda costa”. Margaret Cavendish lo llevó más lejos: los filósofos, decía, hacen mil distinciones sobre una sola cosa, y acaban por enredarse —y confundirnos— con sus seres, no-seres y seres neutros; con lo corporal y lo incorpóreo, sin que ni ellos mismos, ni ningún otro cuerpo, logren encontrarles algún sentido. Sus distinciones son como los trucos de los ilusionistas: aparecen aquí… y se desvanecen.
Todo cierto. Solo por estas razones, no creo que tenga muchas posibilidades de hacer alguna diferencia en el principal debate actual sobre el tema de este manuscrito, que se podría llamar ontología fundamental, es decir, la crisis de patología social que debilita las democracias y las universidades no es por la pos-verdad, sino por el sesgo cognitivo de no poder reconocer que es lo que hace que una afirmación sea verdadera.
1.2 Modos lógicos
Para orientarnos en la lectura del Crisol de Pensadores, es útil considerar algunos aspectos clave que pueden enriquecer nuestra comprensión y hacer la experiencia de lectura más profunda y significativa:
Inferencia abducción es un tipo de inferencia o razonamiento lógico que se utiliza para formular la mejor explicación posible de un conjunto de hechos o datos observados. A diferencia de la deducción e inducción, la abducción no busca necesariamente la verdad o la probabilidad estadística, sino la explicación más plausible o razonable que justifique las observaciones.
Características de la abducción:
Definición: la abducción es un proceso de inferencia mediante el cual se propone una hipótesis que podría explicar un fenómeno o conjunto de datos observados. Se formula a partir de la observación de un hecho sorprendente o inesperado y busca una explicación plausible.
Certeza: No garantiza la verdad ni la probabilidad alta de la conclusión. Es una conjetura que necesita ser verificada o falsificada posteriormente.
- Estructura:
- Observación: se observa un hecho o fenómeno inesperado.
- Regla: se formula una hipótesis que podría explicar ese fenómeno.
- Conclusión: por lo tanto, la hipótesis podría ser una explicación plausible del fenómeno.
- Ejemplo clásico de abducción:
- Observación: “El césped está mojado”.
- Regla: “Si ha llovido, el césped suele estar mojado”.
- Conclusión abductiva: “Probablemente ha llovido”.
- Uso en la ciencia y la vida cotidiana. La abducción es común en la investigación científica, la medicina, la criminología y en la vida cotidiana cuando tratamos de explicar eventos inesperados. Por ejemplo, los médicos usan la abducción cuando diagnostican una enfermedad a partir de síntomas observados, proponiendo la enfermedad que mejor explique los síntomas.
- Comparación con otros tipos de inferencia:
- Deductiva: La conclusión se deriva lógicamente de las premisas.
- Inductiva: Se generaliza a partir de casos específicos para llegar a una conclusión probable.
- Abductiva: Busca la mejor explicación posible de un conjunto de datos, pero no garantiza la verdad de la hipótesis.
La diferencia principal entre una inferencia inductiva y una inferencia deductiva radica en la forma en que se relacionan las premisas con la conclusión y en el grado de certeza que proporcionan:
Inferencia deductiva
Definición: una inferencia deductiva es un tipo de razonamiento en el que la conclusión se deriva necesariamente de las premisas. Si las premisas son verdaderas y el razonamiento es válido, la conclusión también debe ser verdadera.
Certeza: Proporciona certeza lógica. La conclusión es una consecuencia directa y necesaria de las premisas.
- Estructura: se basa en una estructura lógica que sigue reglas estrictas. Por ejemplo, un silogismo clásico:
- Premisa 1: Todos los humanos son mortales.
- Premisa 2: Sócrates es humano.
- Conclusión: Por lo tanto, Sócrates es mortal.
- Características:
- Va de lo general a lo particular.
- Es imposible que la conclusión sea falsa si las premisas son verdaderas.
Inferencia inductiva
Definición: una inferencia inductiva es un tipo de razonamiento en el que la conclusión se infiere de las premisas, pero no se sigue necesariamente de ellas. Se basa en la observación de casos específicos para llegar a una conclusión general.
Certeza: proporciona probabilidad, no certeza. La conclusión es plausible pero no garantizada, incluso si las premisas son verdaderas.
Estructura: se basa en la acumulación de evidencia observacional. Por ejemplo:
- Premisa 1: El sol ha salido por el este todos los días hasta ahora.
- Conclusión: Probablemente, el sol saldrá por el este mañana.
- Características:
- Va de lo particular a lo general.
- La conclusión puede ser falsa incluso si todas las premisas son verdaderas, porque se basa en la probabilidad y la generalización.
Resumen de la diferencia:
Inferencia deductiva: la conclusión sigue necesariamente de las premisas. Si las premisas son verdaderas, la conclusión debe ser verdadera.
Inferencia inductiva: la conclusión es probable y se basa en la observación de patrones o tendencias. La conclusión no es necesariamente verdadera, aunque las premisas lo sean.
En pocas palabras, la deducción busca certeza absoluta a partir de premisas, mientras que la inducción busca probabilidades basadas en evidencia empírica.
La lógica del conocimiento: epistemología
En Laws and Symmetry, Van Fraassen sostiene la idea de que las consideraciones explicativas que guían nuestras creencias, de alguna manera, forma y hasta cierto punto, nos parecen algo natural e inmediato. Una vez que comenzamos a prestar atención al razonamiento diario en la discusión académica y el debate público, notamos la frecuencia con la que las cosas fluyen por el convencimiento de motivos explicativos.
Van Fraassen había presentado algunos argumentos aparentemente ineludibles en el sentido de que el razonamiento abductivo debía evitarse, so pena de irracionalidad. Tal vez nosotros, los filósofos y los teóricos de la biología moderna, tendemos a confiar en esta forma de razonamiento con el fin de generar teorías explicativas para problemas complejos, pero eso no lo hace correcto. Hay todo un catálogo de sesgos y decisiones sistemáticas de los sistemas normativos que los estudios experimentales han demostrado. Dejar que las consideraciones explicativas impacten nuestras creencias también podría formar parte de estos sesgos.
La crítica de Van Fraassen al razonamiento abductivo se produjo como parte de una defensa de la epistemología bayesiana, que en el momento de sus escritos era todavía una “epistemología subterránea[7]”. Sin embargo, esa epistemología pronto se convertiría en “todo el furor” y ha dominado fuertemente nuestro pensamiento sobre la confirmación, la racionalidad y la revisión de creencias durante las últimas dos décadas. Con la creciente popularidad de la epistemología bayesiana, que motivó que la revista Nature advirtiera sobre la necesidad de abandonar la metodología de pruebas de hipótesis por valores P, surgieron nuevos argumentos que pretendían demostrar que cualquier forma de razonamiento que se desviara del camino bayesiano de la sabiduría, como la abducción, presagiaba un comportamiento epistémico irresponsable. Después de esa crisis, quedó claro que la lógica de la abducción está perfectamente en orden[8].
La educación, cuando realmente es, ha sido sugerida por la comunidad científica como aquella que se basa en procesos de disertación en los cuales los estudiantes aprenden a justificar, categorizar, modelar, demostrar, explicar, fundamentar, discutir, debatir y sintetizar… La sabiduría que poseemos los mortales no consiste simplemente en recordar las cosas pasadas y vertidas en las aulas sin una reflexión profunda, sino en ser capaces de crear predictores, lo cual se considera la forma de validar la solidez de las teorías científicas modernas. Esto es visto por los pensadores como la forma más elevada de inteligencia humana[9].
El tipo de inferencia abductiva que se basa en consideraciones explicativas emite juicios sobre la calidad de las explicaciones científicas y filosóficas y, en última instancia, sobre la superioridad explicativa, aspectos cruciales para decidir qué creer y cómo cambiar nuestras creencias. Es posible que hayas escuchado algunas cosas buenas sobre este tipo de inferencia, pero también, más probablemente, algunas críticas negativas, y es posible que te preguntes qué hacer con ellas o cómo reconciliarlas. Si buscas rigor en el pesar, te animo a que sigas este tema, ya que hay evidencia acumulada de que la abducción y, en general, las consideraciones explicativas juegan un papel clave en muchos procesos cognitivos de alto nivel, incluida la categorización[10], la generalización[11], el máquinas de aprendizaje[12], la compresión[13], interpretación del comportamiento[14], procesamiento semántico[15] y, razonamiento y cambio de creencias[16].
La percepción no es la recepción masiva de información sensorial como ingenuamente podría pensarse, sino que implica una diferencia activa, aunque típicamente inconsistente: una torre que vemos a lo lejos proyecta solo una imagen diminuta en nuestras retinas. Si percibimos la torre como alta, eso es la base de la imagen en la retina y una estimulación de la distancia entre nosotros y la torre. A este respecto, John Stuart Mill llama inferencia inductiva[17]. Eso puede ser ya una apelación implícita a la abducción, dado que si Gilbert Harman tiene razón en que la inducción es un tipo especial de abducción[18]. Dejando por un momento la relación entre inducción y abducción, obsérvese los pasajes que sugieren que hay una clara conexión entre la percepción y el razonamiento explicativo. Se atribuye la ocurrencia de ambigüedad perceptiva: cuando varias interpretaciones de una impresión son posibles; al hecho de que una persona puede vacilar entre diferentes explicaciones.
La relación entre percepción e inferencia, que es más explícita al relacionar la percepción directamente con la explicación. El razonamiento explicativo ayuda a resolver casos de ambigüedad perceptiva. La hipótesis de lo que percibimos está guiado por un razonamiento explicativo. Más exactamente, esta afirmación, respaldada por referencias a los resultados de experimentos de Irwin Rock[19], la mejor percepción en la que nos establecemos es la que ofrece la mejor explicación del estímulo. Estos efectos incluyen el movimiento estroboscópico, en el que un objeto estacionario parece moverse; la percepción anortoscópica de la forma, en la que percibimos un objeto al ver solo pequeñas partes a la vez; y el efecto de profundidad cinética, que nos permite interpretar las proyecciones de objetos tridimensionales en una pantalla como sombras de objetos tridimensionales, en lugar de como transformaciones de objetos bidimensionales. Se sondean otras posibles explicaciones para estos y otros efectos empíricos, como la interpretación de que es una mera cuestión de frecuencia de exposición previa y el punto de vista de la constancia, que nos permite preferir la interpretación que mantiene el percepto constante a través de cambios de ángulo de visión. Sin embargo, se argumenta que su propuesta ofrece una mejor explicación para esos efectos que los relatos de la competencia. Por lo tanto, se argumenta que la abducción está a favor de una teoría de la percepción que reconoce paquetes estructurados de información.
Los juicios sobre la calidad de la explicación suelen ser relativos a los supuestos de fondo, y precisamente porque los objetos, normalmente, el estímulo presentado se explica mejor, pero ese estímulo es anulable cambiando la explicación. Estas ideas de las ilusiones ópticas son particularmente interesantes porque, a menudo, se ha alegado que la ilusión proporciona evidencia a favor de la hipótesis del cerebro bayesiano, según la cual el sistema nervioso humano funciona en gran medida como si obedeciera a las prescripciones de asignar probabilidades a las hipótesis sobre lo real. Desde esta perspectiva, la ilusión pone de relieve que siempre partimos de probabilidades previas o simplemente a priori: cuando el cerebro calcula la percepción a partir del estímulo, asigna un alto valor a la hipótesis de la luz que modifica la profundidad de los objetos. Jakob Hohwy hace un argumento a favor de este enfoque bayesiano de la percepción, aunque enfatiza la importancia de la abducción para su caso, la ve como un principio esencialmente bayesiano[20]. Sin embargo, la afirmación no es tan fácil de sostener como él podría pensar. Según todos los signos, la mente cognitiva está hasta los oídos en abducción. En su opinión, eso hace que las perspectivas de un progreso real en la ciencia cognitiva sean tenues, porque no sabemos cómo funciona la abducción y, por lo tanto, no sabemos cómo funciona la mente cognitiva. Si bien no sabemos mucho sobre la abducción, esto también obstaculiza el progreso en la ciencia cognitiva.
Si eres científico o pretendes ser un pensador agudo, es fundamental determinar lo que un hablante quiere decir con un enunciado. Específicamente, se ha argumentado que la decodificación de enunciados es una cuestión de averiguar la mejor explicación de por qué alguien dijo lo que dijo cuando lo dijo. Incluso más específicamente, los autores que trabajan en el campo de la pragmática han sugerido que los oyentes invoquen las máximas griceanas de la conversación para ayudarlos a deliberar sobre si el contenido semántico del enunciado es lo suficientemente informativo para los propósitos de la conversación, o si es demasiado informativo, está fuera de tema o es inverosímil. De otra manera, es extraño o inapropiado. Lo que hace la pragmática es proporcionar un conjunto de principios explicativos que restringen la interpretación o producción de un enunciado cuya representación lingüística ya ha sido conocida previamente. Para entrar en un poco más de detalle, la pragmática parte de la observación de que los enunciados verdaderos aún pueden ser engañosos. El contenido semántico del enunciado de un hablante puede ser P, pero si la mejor explicación de por qué hizo el enunciado en la ocasión dada es, o implica, que también quería transmitir Q, entonces su enunciado puede ser engañoso incluso si P es verdadero, porque Q puede ser falso.
Por ejemplo, normalmente interpretamos los enunciados:
1) Algunos de los invitados traen flores.
Como implicando que no todos los invitados traen flores. Después de todo, si fuera el caso, sería difícil explicar por qué el orador no dijo simplemente que todos los invitados traen flores. Por lo tanto, si todos los invitados traen flores, entonces el hablante no está diciendo nada falso. O supongamos que un estudiante de posgrado le dice a su asesor:
2) Usted ha publicado algunos trabajos que realmente me gustan.
El asesor puede ver dos posibilidades de por qué el estudiante pronunció esta frase. Una es que el estudiante quería transmitir que leyó algunos de sus trabajos y que le gustaron todos los que leyó; la otra es que leyó algunos o todos sus trabajos y le gustaron algunos de los que leyó y otros no tanto. Dependiendo del contexto, puede aparecer una u otra explicación para el asesor. Naturalmente, las dos explicaciones pueden estar estrechamente en competencia, en cuyo caso la inferencia de una implicación puede ser reservada en el mejor de los casos. Esto explica por qué las implicaciones pueden variar en fuerza. El grado en que una explicación se destaca como la mejor tiene un impacto significativo en la disposición de las personas a inferir la verdad de esa explicación.
Si eres científico, filósofo o poeta, es probable que no necesites estar convencido de la importancia de la abducción, dado lo común que es trabajar en apelaciones de explicación en estas formas de conocimiento. Los sociólogos han argumentado que nuestra confianza en el testimonio de otras personas se basa en el razonamiento abductivo[21]. La mejor explicación de por qué el informante afirma P es, normalmente, que lo cree por razones debidamente responsables y tiene la intención de que nosotros también lo creamos. Es por eso que, normalmente, estamos justificados para confiar en el testimonio de un informante.
Algunos pensadores consideran que es mejor la metodología abductiva que la ciencia proporciona; incluso llegan a llamar a la abducción la inferencia que hace la ciencia[22]. Otros creen que la lógica deductiva, para situaciones causa-efecto, es superior en sus metodologías[23]. En relación con esto, se ha dicho que la abducción es el modo de razonamiento médico de diagnóstico: los médicos y los QFB tienden a optar por la hipótesis que mejor explica los síntomas del paciente[24].
Si la abducción es tan ubicua, desempeña todos estos roles en la vida cognitiva de las personas y posee las características mencionadas, ¿por qué sabemos tan poco sobre ella e, incluso, tal vez no tenemos idea de cómo funciona? Cuando se nos presiona, podemos tener dificultades para explicar qué es exactamente una abducción. Incluso los psicólogos pueden estar interesados en diversas cuestiones descriptivas en torno a este concepto. Sin embargo, el auge de la estadística bayesiana plantea la pregunta de por qué deberíamos seguir preocupándonos por el estatus normativo de la abducción. De hecho, a la luz de los éxitos que puede reivindicar la estadística bayesiana, cualquier afirmación sobre la contribución del estudio de la abducción al progreso de la ciencia podría parecer exagerada, e incluso ridícula[25].
1.3 Comprensión reflexiva
La lucha de los seres humanos por integrar una comprensión reflexiva del mundo, tal como lo describe la ciencia, y la ambiciosa esperanza de florecimiento humano, como lo describe la poesía y la filosofía, es algo en lo que los humanos han fracasado en gran medida en los últimos trescientos años: antropoceno. El pensador universitario es muy serio acerca de la ciencia y muy serio acerca de los seres humanos en sus esperanzas y temores. Es necesario un compromiso más profundo con el arte de pensar y las creaciones literarias y sus consecuencias. Cuando los seres humanos reflexionan sobre lo que más les importa en la vida, probablemente estén pensando en un aspecto del florecimiento humano. La mayoría de las personas quieren vivir vidas prósperas y desean que aquellos a quienes aman también prosperen. Pero hay muchas cosas que dificultan el florecimiento en tiempos de incertidumbre. Es estresante tener expectativas de ser capaz de controlar el propio destino, especialmente cuando solo se basan en suposiciones que resultan ser infundadas en la razón más objetiva. El florecimiento humano tiene que ser robusto frente a las incertidumbres en nuestro conocimiento sobre el presente y nuestras predicciones sobre el futuro. Para florecer, se requiere una visión científica y la mejor sabiduría que la poesía y la filosofía puedan darnos (llamamos florecer espiritualmente a confiar en la poesía y la filosofía). Para algunos, aún no son compañeros de las noches de lectura. Podríamos pensar en la frase escrita en la UNAM: “Por mi raza hablará el espíritu”, el despertar de una larga noche de opresión: Vasconcelos. La palabra espíritu pertenece a una era precientífica pasada y podría pensarse que la ciencia tiene poco que decir sobre las decisiones más importantes de la vida. Rechazamos ambas posiciones. Vemos gran necesidad de agenciar conocimiento científico para ayudar a enfrentar los mayores desafíos de la humanidad, y también vemos una gran necesidad de sabiduría espiritual para usar bien los frutos de la ciencia y abordar cuestiones que se encuentran fuera del alcance autolimitado de la ciencia. Creemos que el vivir bien se ve facilitado por un respeto armonioso por las contribuciones de la investigación y la experiencia humana.
Antes de que se puedan tomar decisiones acertadas en la vida, primero es necesario identificar cómo sería un buen resultado. Eso significa saber qué significa para los humanos prosperar. Considere que hay tres dimensiones del florecimiento humano que no pueden separarse, pero que pueden distinguirse con el propósito de considerarlas. La primera es material, porque los seres humanos no pueden prosperar sin bienes ecológicos para ellos mismos y sus familias. La segunda es relacional, porque los seres humanos no pueden prosperar aislados; necesitan estar con los demás y hemos evolucionado para relacionarnos con los demás. La tercera es trascendental, porque solo con lo material y lo social todavía falta algo, sin lo cual los seres humanos experimentan una especie de pobreza espiritual. Estas dimensiones están conectadas, porque cada una de ellas se expresa a través de la otra en el arte de vivir.
El florecimiento humano no está suspendido en el aire, sin medios visibles de sustento, y sujeto solo a los caprichos de las modas intelectuales y morales. Identificamos los pilares ya citados como la plataforma estable para el progreso humano. El ser humano no puede vivir en un espacio de posverdad (engaños y mentiras), porque necesita saber para qué está aquí; y significado, porque los seres humanos desean llevar vidas significativas. Los seres humanos no prosperan si viven de maneras que son falsas, sin objetivos o sin sentimientos a favor. La verdad, el propósito y el significado implican una combinación juiciosa de realidad objetiva científica y respuesta subjetiva poética y filosófica.
Los tiempos inciertos en los que vivimos presentan contextos cambiantes para el florecimiento humano en los que los enfoques anteriores deben orientarse o, al menos, aplicarse de nuevo. Nos centramos en tres casos diferentes de cambio contemporáneo en el mundo, con la intención de que nuestra selección sea más ilustrativa que exhaustiva. Hay una creciente conciencia de la imprevisibilidad de la vida, que se revela por la forma en que las ciencias sociales están reconociendo modelos más complejos en sus matemáticas, y más moralmente cargados de motivaciones e interacciones humanas. Hay patrones cambiantes con el surgimiento de jóvenes que desean un mundo completamente nuevo para sus vidas. El ritmo de la innovación tecnológica se está acelerando con la Inteligencia Artificial, el aprendizaje de máquinas y la síntesis de genes, lo que exige a gritos principios generales que guíen su uso. Esperamos que la biótica que atiende ecosistemas, la biología sintética y una pedagogía con justicia epistémica pronto florezcan en las universidades; todo lo que necesitamos es progreso ético. Una frase que abarca demasiado puede terminar en poco; el florecimiento humano es suficiente para llevarnos lejos. Nuestra esperanza es que al menos exista libertad académica, para educar los pilares sólidos que han demostrado que pueden trabajar juntos y resistir las formas de autoritarismo más salvajes que lastiman la vida. En el mejor de los casos, la literatura es ese puente entre pilares; la humildad intelectual es el medio esencial para el florecimiento humano.
¿Qué estamos destinados a ser?
¿Y por qué estamos tan lejos de lo que estamos destinados a ser?
El término “felicidad” es menos adecuado que el de “florecimiento humano” para dar un sentido contemporáneo a la buena vida. ¿Qué hace que una vida humana sea una vida floreciente? Partimos de que cada persona tiene la misma dignidad, una premisa compartida por las tradiciones filosóficas y religiosas. Posiblemente, desde que los humanos fueron capaces de hacer esta pregunta por primera vez, desde los albores de la historia, se han cuestionado por qué estamos aquí y qué implica una buena vida. Gran parte de la humanidad encuentra un último significado y propósito en la religión. En cualquier caso, los individuos, la comunidad y los gobiernos todavía tienen que tomar decisiones sobre lo que la gente quiere y necesita de la vida expresada por valores epistémicos (la verdad, la demostración, la justificación, el peso de la evidencia, los modos de conocimiento) y valores estéticos del arte.
El florecimiento es un concepto útil dentro del cual considerar tales preguntas, ya que contiene respuestas de sentido común, así como otras que se remontan a los nacimientos de las principales religiones del mundo y a los orígenes de la filosofía. En nuestro momento más optimista, esperamos que lo que escribimos ayude a algunos a llevar vidas más prósperas. No somos tan ingenuos como para imaginar que no estamos escribiendo autoayuda. Creemos que en este momento todos estamos bombardeados con mensajes sobre lo que debemos o no hacer para vivir de manera saludable, lograr equilibrio mental, social y personal, y encontrar significado en la vida; pero no son consideraciones cuidadosas de las contribuciones de las fuentes de conocimiento científico, filosófico y poético. La humildad intelectual y su sabiduría son el florecimiento humano desde un nuevo ángulo, el progreso ético.
En su mayoría, no se está convencido de que la ciencia tenga algo que decir a este respecto. Los valores científicos de cooperación, consenso, reconciliación bioética con ecosistemas y, formas bayesianas de cambiar nuestras creencias para adoptar una posición más objetiva contribuyen a manejar los sesgos y permiten que cada uno haga del florecimiento un recurso evolutivo en el tiempo. Esta posición —ser feliz— es un progreso permanente de renovación de significado y proporciona un marco valioso dentro del cual considerar la importancia de satisfacer los anhelos de bienes materiales, relaciones exitosas y la esperanza de experimentar sentidos más grandes que nosotros mismos: lo trascendente. Lo trascendente no solo es religioso; el arte, la naturaleza salvaje y la consideración de nuestro hogar en el cosmos son ejemplos de caminos de trascendencia. Juegan un papel particular dentro de las religiones y filosofías que se abren a través de una perspectiva ética: “por mi raza hablará el espíritu”, el despertar de una larga noche de opresión, como diría Vasconcelos.
Las palabras importan. Dentro del materialismo, la energía, las ondas, la materia, los ecosistemas y la biología se refieren a un materialismo que podría ser un acceso razonable a la salud, agua, aire, suelo, y un hogar seguro y estético, para no estar en constante preocupación por asuntos financieros. El florecimiento humano exige un concepto amplio de la dimensión material para no definir al ser humano como un ser de paja. Una de las características más tristes es asumir que los ecosistemas y la vida salvaje nos pertenecen para consumirlos y explotarlos sin límites éticos. No se trata solo de cursos de reflexión sobre ser respetuosos con los animales no humanos; gran parte de la vida moderna, incluida la educación, sufre de la banalidad del reduccionismo vulgar que intenta simplificar problemas complejos e irreductibles para su comprensión y solución. Ese enfoque vulgarmente reduccionista da la impresión de que todo lo que hay en la vida es progreso material. La dimensión material sí importa, de hecho, si la pensamos en dormir lo suficiente y disfrutar de una salud razonablemente buena, las cosas materiales importan.
La mayoría de nosotros disfrutamos de la compañía de los demás, incluidas nuestras mascotas y árboles; incluso si hay momentos en los que preferimos estar solos, estamos acompañados por productos culturales como la literatura, el cine, la música, los videojuegos y las redes sociales. Valoramos la familia y la amistad. A lo largo de nuestra vida llevamos material genético de dos individuos; durante nueve meses, más o menos, dependemos del entorno biológico que proporciona uno de nuestros padres. Esta primera relación es importante. Si todo va bien, el bebé nace después de haberse desarrollado, y, capaz de respirar y alimentarse, comenzará a crecer hasta llegar a la edad adulta. La relación afectiva de una madre con su hijo ilustra cómo la distinción entre las dimensiones materiales y sociales del florecimiento humano puede no ser siempre clara. La protección de la comunidad, el estado de derecho, la cooperación, la democracia y el consenso nos hacen pensar que la educación extrapola la importancia de vivir en sociedad. Además, un ecosistema sano y la socialización con animales de compañía juegan un rol importante en el disfrute, la seguridad y la salud mental como productos de una relación social.
Para la mayoría de nosotros, hay momentos en los que los aspectos de la vida parecen ir más allá, trascender lo cotidiano y lo mundano. La naturaleza del arte, la ciencia, la poesía, la ingeniería, la música y las matemáticas puede transportarnos más allá de nosotros mismos. Las personas creativas, sea cual sea su disciplina, pueden sentir que al menos parte de lo que hacen es traer alegría a los demás y aportar prosperidad y riqueza cultural a sus vidas. Para nosotros, la dimensión trascendente del florecimiento humano es tan significativa como lo material y lo social. Lo que nos hace humanos es la capacidad de educarnos, de pedir ayuda, de florecer en un espacio de verdad objetiva y paz, y de colaborar en sociedad para el progreso ético.
1.4 La verdad
Tomamos como axiomático que una vida floreciente se construye sobre la verdad. Pilato preguntó: “¿Qué es la verdad?”. Sea lo que sea lo que quiso decir con esto, la pregunta sigue siendo importante. En el contexto de una resaca post-positivista y una enfermiza política de posverdad, es difícil asumir que la única verdad que importa es la verdad empírica: aquella de las afirmaciones sometidas a diseños experimentales, solidez teórica, capacidad predictiva y explicativa. Pero hay otros modos de verdad. El matemático establece la verdad asegurándose de que sus afirmaciones caen dentro del dominio de las matemáticas consistentes bajo demostración. La verdad también la podemos encontrar en otros dominios culturales, como la historia, la estética, la literatura y la filosofía moral.
1963, la cuarta transformación en el crisol de pensadores: cultura precolombina, colonialismo, positivismo y racionalismo en la ciencia. El sueño de Eli de Gortari[26].
“Tengo 24 años y todavía no he hecho nada… estoy seguro de que no es por nada que he estado luchando con mis dudas y pasiones por los últimos ocho años. Pero, ¿Para qué estoy destinado? Solo el tiempo lo dirá”. León Tolstói
“El que no arriesga nada, no hace nada, no tiene nada, no es nada y se convierte en nada, puede evitar el sufrimiento y la tristeza, pero simplemente no puede aprender, sentir, cambiar, crecer ni amar. Encadenado por su certeza, es un esclavo; ha perdido su libertad. Solo quien arriesga es verdaderamente libre”. Leo Buscaglia
La ciencia intenta movernos hacia una mayor objetividad, responder a percepciones dándonos una idea de cómo esta experiencia trasciende nuestra percepción cotidiana del mundo, aspira a una compresión más congruente de nosotros mismos, así como responder a la naturaleza del conocimiento.
Independientemente de que está afuera o no, la forma correcta de ver las cosas, lo más importante que hay que reconocer aquí es que el prejuicio contrario típico de nuestro tiempo —que la materia gobernada por leyes puramente por ecuaciones (leyes naturales) y no mentales es la base de toda la realidad, incluida la mente— no es ni más racional ni más empíricamente plausible. De hecho, el argumento será que es, de lejos, la posición más inverosímil que se ofrece. Aun así, el materialismo es la presuposición que ha molado una influencia tan poderosa sobre las mentes de muchos filósofos y científicos hoy en día que continúan adhiriéndose a él incluso cuando la evidencia y la razón por igual parecen instar a su abandono. Ninguna afirmación, por exorbitante o incluso aparentemente perversa que sea, es tan extrema que algún filósofo comprometido con una explicación enteramente “fisicalista”, “naturalista” o “materialista” de la mente no la haya propuesto. Incluso la afirmación de que todos los fenómenos mentales que la mayoría de nosotros consideramos indudables —como la conciencia, la racionalidad y la intencionalidad— son, de hecho, algo que no existe. Sería difícil exagerar la fanática que puede llegar a resultar esta devoción a un materialismo esencialmente mecanicista que deja fuera de la existencia la conciencia y la información de códigos que estructuran la realidad.
Por lo demás, personas aparentemente sensatas e inteligentes presentan regularmente argumentos que, de no ser por su profunda y ferviente fe en una imagen materialista de la naturaleza, indudablemente reconocerían como absurdos y circulares. Algunos están dispuestos a conceder que lo evidente de los fenómenos de la conciencia y la vida mental es irreducible al mundo fisicalista. En lugar de admitir que el materialismo ha fallado ante la evidencia empírica, concluyen que dicha evidencia debe ser rechazada por no haber superado la prueba de su metafísica. Este es el peligro de cualquier ideología: el poder de determinar nuestra visión del mundo antes de que hayamos vuelto nuestros ojos hacia él. Por regla general, en filosofía y ciencias, cuando una teoría no logra explicar un fenómeno, es la teoría la que debe ser eliminada; solo en la ciencia de la mente es rutinario que el fenómeno sea eliminado en favor de la teoría. Esto habla de un problema de sesgo, mucho más grave que la mera indolencia intelectual, como si el observador científico estuviera contemplando el cosmos desde fuera del cosmos. La falta de humildad intelectual en los idealistas es el efecto de un trágico cautiverio de la razón a un dogma árido: el fin de la historia de las ideas[27].
Desde el idealismo, la visión de George Berkeley de que toda realidad fenoménica no es otra cosa que una colección de impresiones mentales, inherentes a ningún sustrato material, sostenidas en ser y orden coherente únicamente por la voluntad De Dios, y desprovisto de cualquier poder causal independiente; en esta visión de las cosas somos realmente almas incorpóreas, —o en todo caso, almas cuyos cuerpos son inmateriales— que simplemente participan por gracia de Dios del sueño de un mundo material. Por error se nos dice que debemos obligarnos a decidir entre dos Imag1 mecanicistas diferentes: Materialista de una máquina cósmica que genera agencia mental o una imagen cartesiana que postula que no hay conexión biología entre cuerpo y mente.
Rechazamos la visión de la mente como algo pensante intrínsecamente incorpóreo e inextenso, en asociación puramente intrínseca con un orden material mecánico. También rechazamos toda teoría que sugiera lo emergente de la mente a partir de una realidad no mental, como si fuera una especie de “propiedad” física inherente a un reino material que, en otros aspectos, funciona mecánicamente. Nuestra posición es que la vida es, en sí misma, una lógica “orgánica” omnipresente del orden material desde el principio, no emergiendo de ese orden, sino creándolo, gobernándolo, formándolo y vivificándolo desde adentro mediante la razón. La vida y la mente son ambas irreductibles; el lenguaje es esa combinación, un aspecto más de un mismo fenómeno irreductible en términos mecanicistas. Una fenomenología verdadera de la agencia mental revela un compromiso absoluto de la mente en un acto infinito de conocimiento que es nada menos que la fuente y el fin de estas tres realidades, y de hecho de todas las cosas; todos los actos de la razón son participaciones en la conciencia del cosmos.
1.5 Sesgo: un punto ciego
Un sesgo implica una desviación sistemática de una norma o estándar genuino de corrección. Cuando se considera que las personas son sesgadas, es porque se apartan sistemáticamente de ciertas normas o porque están dispuestas a hacerlo. Ciertamente, este pensamiento central puede considerarse útilmente como una especie de generalización o abstracción de las nociones más específicas de sesgo que están en juego en varias disciplinas, así como algo que es fiel a mucho de lo que decimos y pensamos sobre el sesgo en la vida cotidiana. Tomando la noción de sesgo tal como se entiende en estadística, es la tendencia a una desviación sistemática de una norma o estándar genuino de corrección[28]. Cuando las personas se consideran sesgadas, es porque se apartan sistemáticamente de ciertas normas epistémicas o están dispuestas a hacerlo. Este pensamiento central puede considerarse en juego en varias disciplinas (química, biología, psicología, estadística, economía, historia, física), así como algo fiel a mucho de lo que decimos y pensamos sobre el sesgo en la vida cotidiana. En estadística, el sesgo es la tendencia a sobreestimar o subestimar el valor real de algún parámetro[29].
En el contexto estadístico, la norma o estándar relevante es la verdad o la exactitud, y algo cuenta como sesgo en virtud de apartarse de la verdad o del valor real de una manera que no es sin patrón, impredecible o aleatoria. Es confundir correlación con causalidad. Es el caso en que la norma relevante es la verdad o la estimación precisa. Es necesario establecer una distinción intelectual entre sesgo y error aleatorio o ruido para tratar de corregir el habitual desequilibrio de atención hacia el primero a expensas de los segundos[30].
En un ejemplo de tiro con arco, el éxito consiste en dar en el blanco. ¿Qué es análogo a dar en el blanco cuando se trata de sesgo? Como hemos dicho ya, en muchos casos la norma o criterio de corrección pertinente a la exactitud es la verdad o la estimación precisa. Sin embargo, aunque la verdad es a menudo una norma importante, en muchos contextos la norma relevante que determina si algo cuenta como sesgado puede no tener nada que ver con la verdad o la precisión. Muchos científicos sociales y economistas piensan que lo que gobierna la acción racional es la maximización del valor esperado. Entonces, de acuerdo con la explicación teórica de la norma del sesgo, una persona podría contar como sesgada en virtud de su tendencia a apartarse sistemáticamente de criterios ontológicos y de criterios de causalidad. Muchos sesgos conductuales pueden entenderse como tendencias a apartarse de la norma de maximizar el valor esperado, al igual que muchos sesgos cognitivos pueden comprenderse como tendencias a apartarse de la norma epistemológica de la verdad o la precisión[31].
En el mundo moral, el sesgo puede referirse a consideraciones respecto al respeto al que toda persona tiene derecho. Una persona que regularmente no trata a los demás con el respeto que merecen viola una norma moral importante y está debidamente sujeta a críticas por ello. Esto no se deduce simplemente de ser imparcial. Más bien, es una cuestión de prejuicios relacionados con el sexo, la edad, la raza, la clase, la escolaridad, la economía o el autoritarismo. Es probable que, debido a estos puntos ciegos, la persona viole sistemáticamente el respeto, descalificando con violencia al otro. En este caso, sus desviaciones de la norma ética relevante exhiben un patrón sistemático inapropiado, y podemos atribuirles a esos puntos ciegos sesgos raciales, sexistas, de edad, según sea el caso. Es decir, abductivamente, la explicación de las variables estadísticas debe guardar coherencia con hechos, leyes naturales, normas éticas y axiomas matemáticos.
De acuerdo con la explicación teórica de las normas sobre el sesgo, los sesgos suelen implicar desviaciones sistemáticas de las normas. Como se observa a menudo, el término “norma” es ambiguo en múltiples sentidos[32]. ¿Qué sentido del término es relevante aquí? En primer lugar, el sentido relevante no es el de una norma estadística (como datos fuera de lo habitual). En segundo lugar, el sentido relevante de “norma” tampoco es el que está en juego en la literatura académica sobre las “normas sociales” o las “normas de género”, según las cuales las normas son, a grandes rasgos, una cuestión de reglas, convenciones o expectativas no escritas de una sociedad dada sobre cómo debería comportarse la gente. Sin embargo, incluso si una persona pertenece a una sociedad en la que esa norma prevalece, no se deduce de los roles que desempeñan las personas que lo equitativo no esté sesgado. Por el contrario, su división igualitaria del trabajo bien podría reflejar una falta de sesgo sobre estos asuntos. Del mismo modo, cualquier artista pionero, creador de tendencias o iconoclasta se apartará sistemáticamente de las normas prevalecientes en el sentido de las expectativas comunes sobre el comportamiento, pero no está sesgado por ese motivo.
Contrasta el sentido de “norma” en el que muchos de nosotros pensamos que es una norma genuina que las personas deben ser tratadas con respeto. En este sentido del término, si es una norma moral genuina dice que las personas deben ser tratadas con respeto, entonces tenemos buenas razones para tratarlas de esta manera, y deberíamos. En este sentido, la verdad de la afirmación de que tratar a la persona con respeto es una norma genuina no depende de la frecuencia con la que las personas sean tratadas de esta manera en la práctica (incluso si es común que las personas sean tratadas con falta de respeto, eso no tiende a mostrar que no es una norma genuina), o de cómo encaja con las reglas no escritas y las expectativas sociales que prevalecen en una sociedad determinada. Incluso en una sociedad en a la que se considera respeto argumentar alienados con el dogma de devoción a la autoridad, esto es consistente con la idea de que esos miembros deben ser tratados con respecto. De acuerdo con la explicación de la teoría de la norma sobre el sesgo, cuando alguien está debidamente sujeto a la crítica como sesgo, esto implica que se aparta sistemáticamente de una norma genuina en este sentido.
Aunque las normas morales genuinas proporcionan un paradigma del tipo relevante de norma, son una especie de un género más inclusivo. Muchos economistas sostienen que maximizar el valor desde el punto de vista del agente es la norma de la acción racional. Si es así, entonces uno puede considerarse sesgado al apartarse de esa norma de ciertas maneras sistemáticas. Aquí, la norma relevante es, al menos en primera instancia, una norma de racionalidad práctica en oposición a la moral. De manera más general, existe una impresionante diversidad de normas en relación con las cuales alguien o algo podría considerarse sesgado, incluidas las normas morales, las normas de justicia, las normas de precisión y las normas de racionalidad teórica y práctica.
Aunque la idea central de que los sesgos implican desviación sistemática de normas genuinas puede parecer familiar, al menos en algunas de sus instancias, sostenemos que, cuando se desarrolla de la manera más plausible en su lógica, tiene implicaciones radicales y de largo alcance. Por ejemplo, sostenemos que tanto la moralidad como la racionalidad a veces requieren que seamos parciales, en el sentido peyorativo de “sesgados” (en los modelos bayesianos). La explicación de la teoría de las normas también tiene implicaciones radicales para la forma en que debemos ver a otras personas y nuestras relaciones con ellas. En muchos casos de desacuerdo, se nos exige racionalmente que veamos a aquellos que no están de acuerdo con nosotros como parciales, incluso si no sabemos absolutamente nada sobre cómo llegaron a sus puntos de vista o sobre sus estados mentales, más allá del mero hecho de que no están de acuerdo con nosotros de la manera en que lo hacen. Apreciar por qué esto es así nos permite ofrecer una explicación convincente de un fenómeno empírico teóricamente interesante y prácticamente importante: el hecho de que las acusaciones de parcialidad a menudo inspiran no solo negacionistas, sino también contraacusaciones de sesgo, en el sentido de que la acusación original de sesgo se debe al hecho de que quienes lo hacen son ellos mismos parciales.
Otro conjunto de aplicaciones de la explicación de la teoría de la norma se refiere al llamado “punto ciego”, o nuestra tendencia a ver el sesgo en otras personas de maneras que no logramos verlo en nosotros mismos. El punto ciego del sesgo ha sido ampliamente documentado y discutido por los psicólogos sociales en un fascinante cuerpo de investigación[33]. Sostenemos que, cuando se desarrolla en su forma más plausible, la explicación de la teoría de la norma ofrece una explicación convincente del punto ciego del sesgo, una explicación que mejora los tipos de hipótesis favorecidas por los psicólogos cognitivos. Esta explicación depende de lo que nosotros llamamos el carácter perspectivo de las atribuciones sesgadas, el cual, tal y como lo entendemos, tiene tanto un aspecto psicológico como un aspecto racional en el que asignamos probabilidad a nuestras perspectivas. Desde el punto de vista psicológico, nuestros puntos de vista sobre un tema —por ejemplo, la política— influyen naturalmente en nuestros juicios sobre el tema, y de maneras predecibles y familiares, estamos en un sesgo inadvertido: el punto ciego.
1.6 Veritistas
La academia valora la verdad. Puede haber razones prácticas, prudenciales o políticas para aceptar una falsedad conocida. Pero se sostiene que nunca puede haber razones epistémicas buenas para hacerlo. Tampoco puede haber buenas razones para aceptar modos de justificación que se sabe que no conducen a la verdad. Tal es el consenso prevaleciente. Aunque parezca razonable, esta postura tiene un defecto fatal. No puede explicar la posición epistémica de la ciencia: porque la ciencia se basa descaradamente en modelos, idealizaciones conceptuales y experimentos mentales que se sabe que no son ciertos. La ciencia moderna es uno d los mayores logros cognitivos de la humanidad. Pensar que este logro es una casualidad sería una locura. Así que la epistemología tiene la tarea de dar cuanta del éxito de la ciencia.
Una ciencia del conocimiento centrada en la verdad —o veritista— debe tratar los modelos, las idealizaciones y los experimentos mentales como heurísticas. Estas son reglas prácticas o métodos informales útiles para enfrentar problemas complejos, mal definidos o con información incompleta. No garantizan una solución óptima, pero permiten avanzar. Son flexibles, rápidas y a menudo dependientes del contexto o de la experiencia previa. Ninguno de estos enfoques es plenamente plausible si se exige verdad literal. No debemos asumir arrogantemente que la inexactitud de modelos e idealizaciones constituye una insuficiencia. Todo lo contrario: sugerimos que su divergencia respecto a la verdad o a la precisión representacional fomenta su funcionamiento epistémico. Cuando modelos o idealizaciones son efectivos —sostengo— son falsedades felices: señales en el camino correcto, aunque no sepamos cuánto falta para la meta. Son componentes ineliminables, valiosos suministros de comprensión.
Las teorías más sólidas deben estar atadas a los fenómenos a los que conciernen, pero niegan que la verdad sea la única atadura aceptable. Se sostiene que las falsedades afortunadas se relacionan con sus objetivos a través de una conexión que proporciona al menos un vínculo tan fuerte y estable con los fenómenos como lo hace la verdad. Aunque los modelos, las idealizaciones y los experimentos mentales son inexactos —a veces tremendamente inexactos—, ejemplifican las características que comparten con sus objetivos y, por lo tanto, brindan acceso epistémico a aspectos de estos que de otro modo se verían eclipsados o subestimados. Son, en cierto sentido, bastante ciertos. Avanzan en la comprensión de los fenómenos que sustentan. Para dar cabida a la ciencia, abogo por pasar a la comprensión de una gama más amplia de fenómenos. En la ciencia y otras investigaciones sistémicas, constelaciones relativamente completas de compromisos epistémicos se mantienen o caen juntas.
Una vez que la verdad es destronada, la conducencia a la verdad también cae. Muchos filósofos sostienen que los argumentos y los métodos se justifican por ser confiables y conducentes a la verdad. Si es así, al desplegarlos y evitar argumentos y métodos que no conducen a la verdad, aumentamos nuestras perspectivas de éxito epistémico. Habiendo dejado la verdad, no puedo sostener tal afirmación. Eso plantea una pregunta importante sobre la normatividad epistémica: si la conducencia a la verdad no reivindica un método o forma de argumento, ¿qué lo hace?
Sostenemos que la aceptabilidad depende de la responsabilidad epistémica más que de la confiabilidad. Representa normas deontológicas. Las normas deontológicas son principios y reglas éticas que regulan el comportamiento profesional de quienes ejercen una determinada actividad, especialmente aquellas que implican una responsabilidad social o moral significativa, como la docencia o la investigación científica. Sostenemos que la aceptabilidad depende de la responsabilidad —un valor epistémico— más que de la confiabilidad. La responsabilidad proporciona criterios de objetividad que se satisfacen mediante representaciones que respetan criterios subjetivos, como las credenciales de verdad: la garantía de que las conclusiones respaldadas por razones objetivas sean verdaderas, es decir, que las conclusiones sean razonables y defendibles en las circunstancias epistémicas.
La posición que emerge no solo asegura la legitimidad epistémica de la ciencia, sino que otorga el mismo estatus al arte. Porque los dispositivos simbólicos que suscriben la aceptabilidad de las falsedades afortunadas en la ciencia también se despliegan en las artes. Por lo tanto, se insta a que las artes encarnen y promuevan la comprensión, y que las artes y las ciencias se entrelacen.
Esta posición reivindica el progreso ético, una afirmación a menudo expresada pero rara vez justificada: que, aunque las obras de arte no son verdaderas, ni siquiera aptas para la verdad, podemos aprender algo importante de nuestros encuentros con el arte.
Al igual que Quine (1961), creo que podemos aferrarnos a cualquier afirmación, pase lo que pase, siempre que estemos dispuestos a hacer ajustes compensatorios en otras partes de nuestro sistema de pensamiento. Uno puede, por ejemplo, seguir insistiendo en que las teorías científicas son inaceptables a menos que sean verdaderas; o que comprender es poder explicar; o que la ciencia es cognitiva pero el arte no lo es. Pero, insisto, el costo de tal tenacidad es sorprendentemente alto. Es lo suficientemente alto como para que sea razonable considerar esta alternativa. Es como intentar descalificar el modelado predictivo como criterio de la solidez de una teoría, aunque no explique por qué el mundo es como es. En este mismo sentido, desvalorizar la contrafactualidad que permite crear moléculas farmacéuticas eficaces, simplemente porque implica aceptar la existencia de múltiples mundos sistemáticos coherentes con nuestras leyes naturales, es un acto de ceguera epistemológica.
Reivindica el valor de lo posible, lo hipotético, lo figurado, y lo emocional como medios legítimos de comprensión. El conocimiento, en esta perspectiva, deja de ser la reproducción objetiva de lo real y se convierte en una red de modos de acceso a lo significativo.
Para dar cabida a los frutos de la ciencia y otras formas de investigación sistemática, es necesario —cómo se ha propuesto— que la epistemología desplace su centro de gravedad del conocimiento hacia la comprensión, en particular hacia lo que se ha llamado comprensión objetual: la comprensión de un tema, práctica o materia[34].
Comprender no es simplemente reflejar. No se trata de creer en una serie de proposiciones individuales justificadas por separado, ni de adherirse a una red coherente de proposiciones interconectadas que representen fielmente los hechos. Comprender un tema implica saber cómo ejercer nuestros compromisos epistémicos para promover fines cognitivos, saber cómo operar dentro de un dominio, plantear preguntas relevantes, trazar inferencias significativas, formular experimentos apropiados. Dado que muchos métodos o normas que guían la comprensión no necesariamente están orientados a la verdad —o no son aptos para determinarla directamente—, la comprensión no es simplemente fáctica. No es un tipo de conocimiento en sentido tradicional; no consiste exclusiva ni principalmente en aceptar verdades, sino en una forma de orientación activa, situada y creativa hacia aquello que se estudia.
La integridad intelectual requiere que ciertos valores —aquellos que sustentan la confiabilidad— sean simultáneamente morales y epistémicos. Dado que la ciencia es una empresa enormemente compleja, exige que los agentes epistémicos trabajen en colaboración para alcanzar una comprensión adecuada de los fenómenos que estudian. Como incluso los mejores métodos están expuestos al error, los mecanismos para identificar, corregir y revisar esos errores deben estar fácilmente disponibles y ser accesibles a toda la comunidad científica.
La mala conducta científica socava profundamente este proyecto común, pues produce resultados no confiables y corroe los fundamentos epistémicos de la ciencia. La confiabilidad, por tanto, no es solo un valor metodológico: es parte integral de la práctica científica. Un científico necesita poder confiar en los hallazgos sobre los que construye su trabajo. De ahí que, al enseñar qué es una buena ciencia y cómo se practica adecuadamente, la educación científica infunda en los científicos noveles ciertas virtudes tanto morales como epistémicas.
Ahora bien, podría objetarse que una responsabilidad meramente epistémica respecto a tales valores es demasiado débil para garantizar la objetividad. ¿Puede una disciplina pretender ser objetiva si reconoce que hay un elemento humano ineliminable en toda afirmación que reivindica su legitimidad?
Sostengo que la objetividad epistemológica que debemos perseguir no es aquella que aspira a una “visión desde ningún lugar” o una “concepción absoluta de la realidad”, como alguna vez pretendió el idealismo o el positivismo lógico. La objetividad, en este marco, no es ausencia de humanidad, sino capacidad para resistir la idiosincrasia, el sesgo y el azar. No eliminamos el elemento humano al definir magnitudes o estandarizar procedimientos de medición; al contrario, la confiabilidad surge cuando una comunidad epistémica asume colectivamente la evaluación crítica de los resultados.
En este contexto, cabe examinar la noción de veritismo, entendido como la posición epistemológica que sostiene que la verdad es condición necesaria para la aceptabilidad epistémica. Aunque esta tesis parece intuitivamente razonable —y es compartida por corrientes como el epistemicismo de la virtud o las teorías del conocimiento primero—, sostengo que el veritismo es insostenible.
¿Por qué? Porque, si asumimos que solo la verdad justifica la aceptación epistémica, entonces no podemos hacer justicia a los logros cognitivos de la ciencia real. Buena parte del conocimiento científico —modelos, aproximaciones, teorías idealizadas— no es estrictamente verdadero, pero cumple funciones epistémicas fundamentales: permite explicar, predecir, intervenir y coordinar prácticas colectivas. Un énfasis excesivo en la verdad impide a la epistemología adaptarse a estas formas genuinas de contribución cognitiva. Catherine Z. Elgin, True Enough (2017): la idea de que la comprensión es más valiosa que la verdad literal.
Sin embargo, los compromisos veritistas son profundos. Renunciar a ellos implica una revisión radical. En particular, propongo desplazar las categorías tradicionales de creencia, afirmación y conocimiento y dar prioridad a la aceptación, la profesión (del compromiso con ciertos valores) y la comprensión. Esta reconfiguración del terreno epistémico libera recursos que las posiciones veritistas no pueden movilizar. Son estos recursos —la confiabilidad, la coherencia práctica, la virtud intelectual, la sensibilidad al contexto— los que deben pasar a primer plano si queremos una epistemología que no esté atrapada por un compromiso inviolable con la verdad, sino orientada al crecimiento del entendimiento.
Según el veritismo, la conducencia epistemológica a la verdad constituye el estándar adecuado para evaluar políticas, prácticas y sus productos. Esta norma se aplica a todos los logros epistémicos —como el conocimiento, la comprensión, la sabiduría o el saber hacer—, ya que el valor epistémico de los métodos utilizados para obtener y evaluar información, así como de los criterios empleados en dichas evaluaciones, es considerado puramente instrumental: se justifican únicamente en la medida en que conducen a la verdad.
Desde esta perspectiva, la replicabilidad de los resultados científicos posee valor epistémico solo si se asume que los resultados replicables tienen una mayor probabilidad de ser verdaderos que aquellos que no lo son. De no ser así —es decir, si los resultados son irreplicables bien respaldados resultaran igualmente confiables—, entonces la replicabilidad perdería su valor como criterio epistemológico relevante.
En este sentido, el veritismo puede entenderse como una forma de consecuencialismo. Sin embargo, se distingue de otras variantes más conocidas de esta corriente en que la consecuencia que busca maximizar no es el placer ni la utilidad, sino la verdad: más precisamente, la promoción de creencias verdaderas o de un conjunto de creencias con predominio de verdad sobre error. Si los veritistas tienen razón, entonces, al menos en la medida en que nuestros fines sean cognitivos, debemos aceptar solo lo que consideramos verdadero, esforzarnos por asegurarnos de que las afirmaciones que aceptamos sean de hecho verdaderas, y repudiar rápidamente cualquier afirmación previamente aceptada al enterarnos de que es falsa.
William James (1951): muchos veritistas sostienen que nuestro objetivo cognitivo primordial es creer tantas verdades como sea posible y no creer tantas falsedades como sea posible. Este es el objetivo con respecto a todos y cada uno de los argumentos individuales. Dicen que nunca es legítimo aceptar una falsedad reconocida, incluso si hacerlo resultara, a largo plazo, en la adquisición de más —o de una mayor proporción de— creencias verdaderas que el repudio de esa falsedad. Este veritismo jamesiano es notablemente tolerante. No discrimina entre creencias verdaderas o falsas. En la medida en que nuestros objetivos son puramente cognitivos, afirma que debemos acumular tantas verdades y tan pocas falsedades como sea posible. Esto se hace fácilmente: toma cualquier número, agrégale un dos. Hazlo otra vez. Y otra vez. Con cada iteración, obtienes otra verdad. El riesgo de aceptar una falsedad en el camino se vuelve cada vez más pequeño. Si prefieres restringir el ejemplo al ámbito empírico, toma cualquier verdad trivial, como “los gatos no crecen en los árboles”. Agrega una disyuntiva (su valor de verdad no importa). Ahora tienes numerosas creencias verdaderas:
Los gatos no crecen en los árboles, o has estado regando ramas con maullidos.
Los gatos no crecen en los árboles, o tal vez los árboles han aprendido a moverse en silencio.
Los gatos no crecen en los árboles, o vives en un mundo donde los frutos persiguen a las aves.
Los gatos no crecen en los árboles, o la naturaleza ha decidido reinventar su catálogo de criaturas.
Los gatos no crecen en los árboles, o tus sueños han echado raíces más profundas que la lógica.
Los gatos no crecen en los árboles, o llevas demasiado tiempo observando sin comprender.
Los gatos no crecen en los árboles, o alguien sembró ternura donde solo debía haber sombra.
Los gatos no crecen en los árboles, o los árboles han empezado a maullar cuando sopla el viento.
Los gatos no crecen en los árboles, o te has vuelto experto en confundir lo real con lo deseado.
Los gatos no crecen en los árboles, o acaso ignoras qué clase de semillas siembra el misterio.
Esto es mucho más fácil y mucho menos arriesgado que, por ejemplo, montar un diseño experimental cuidadosamente controlado, escrupulosamente ejecutado y teóricamente fundamentado. Sin embargo, ejecutar el experimento es epistémicamente más valioso. No servirá insistir en que es probable que el experimento sea más fructífero, al menos si la única forma disponible de medir la fecundidad es contar el número de conclusiones verdaderas o la proporción de conclusiones verdaderas sobre falsas que se pueden extraer. Cada proposición tiene consecuencias inferenciales —de hecho, infinitas consecuencias obvias— por lo que los frutos de las inferencias triviales y los del experimento bien realizado están a la par. Y la automaticidad del procedimiento para generar fragmentos triviales de conocimiento es lo suficientemente eficiente como para empequeñecer el número de verdades que uno podría descubrir al idear y ejecutar experimentos.
Esto sugiere que debemos ajustar el objetivo jamesiano. En lugar de considerar todas las creencias verdaderas a la par, tal vez la epistemología debería distinguir entre creencias significativas y triviales, o entre verdades obtenidas por medios significativos y triviales. Entonces, el veritista jamesiano podría insistir en que nuestro objetivo es creer tantas verdades significativas como sea posible y no creer tantas falsedades significativas como sea posible, o tal vez creer tantas verdades significativas como sea posible y no creer tantas falsedades como sea posible, sean o no significativas (ya que parece epistémicamente objetable creer falsedades, incluso si son triviales). Alternativamente, podría aferrarse a la meta veritista como un fin puramente cognitivo, pero reconocer que, como seres finitos con recursos limitados, necesitamos, por razones prácticas, priorizar algunas verdades sobre otras. No todos los veritistas son jamesianos. Duncan Pritchard se centra en una posición que él llama “T-monismo de valor epistémico”, la visión de que “la verdadera creencia es el único bien epistémico fundamental[35]”. Desde esta nueva posición T-monista, deberíamos preocuparnos por las creencias falsas solo si albergarlas, de alguna manera, interfiere con nuestra acumulación de creencias verdaderas. Se atribuye valor epistémico únicamente a las creencias verdaderas formadas adecuadamente, aquellas que emergen del uso correcto de nuestras competencias epistémicas (basadas en procesos de justificación).
Cuestionamos el igualitarismo inherente a la posición jamesiana, argumentando que se basa en la posición implícita de que dos verdades cualesquiera contribuyen con la misma cantidad de verdad al balance. Esto, afirmamos, es incorrecto. En lugar de preocuparnos por cuántas verdades cree alguien, deberíamos preocuparnos por cuánta verdad cree. Y esto último no es función de lo primero. Las verdades triviales contribuyen poco al cuerpo general de creencias verdaderas de una persona; las verdades significativas contribuyen mucho. Socavar la idea de que necesitamos contar y agregar creencias verdaderas deja de lado la preocupación por la trivialidad. Aun así, se sigue siendo veritista, en tanto se mantiene la convicción de que la verdad es central para la epistemología.
Stephen Hetherington sostiene que debemos tomar en serio la locución “saber mejor” y reconocer que el conocimiento admite grados[36]. Si la creencia de un agente epistémico de que P es verdadera entonces sabe que P de una manera mínima; si tiene alguna justificación para P, sabe mejor que P; y si puede vencer los desafíos escépticos a P, sabe perfectamente bien que P. Pero incluso el tipo más mínimo de conocimiento requiere la verdad. El gradualismo epistémico no resuelve nuestro problema.
La mayoría de los veritistas consideran que el conocimiento es el paradigma del éxito epistémico, donde el conocimiento es una creencia verdadera no fortuita, justificada o confiable. Algunos consideran que el conocimiento es valioso por sí mismo. Otros piensan que el aspecto valioso del conocimiento radica en que encarna la creencia verdadera. De cualquier manera, la razón para favorecer las creencias justificadas (aquellas respaldadas por evidencia suficiente) y las creencias seguras (aquellas resistentes a posibles errores) es que son susceptibles de ser verdaderas. La justificación y la seguridad tienen un valor meramente instrumental. Dado que las proposiciones son el contenido de las creencias y los portadores de los valores de verdad, son lo que se conoce.
Si esto es correcto, el tipo de justificación de interés para la epistemología es, en primera instancia, la justificación de proposiciones individuales. Justificar una proposición dada es inferirla de proposiciones ya justificadas o mostrar cómo la creencia en ella emerge de mecanismos confiables de formación de creencias. S está justificado en creer que P sobre la base de Q, y Q sobre la base de R, y así sucesivamente. En algunos casos, la secuencia termina en proposiciones que no necesitan más justificación; en otros, la secuencia es infinita.
Los holistas tienden a considerar que esta imagen es engañosa. Sostienen que la aceptabilidad epistémica es, en primera instancia, la aceptabilidad de una teoría o síntesis de pensamiento bastante comprensiva: una constelación de compromisos de apoyo mutuo que se relacionan con un tema. Llamemos a tal constelación un discurso, una narrativa. Consiste en argumentos sobre un tema y las razones aducidas para respaldarlos; en las formas en que se pueden usar para respaldar otros argumentos; y en compromisos de orden superior que especifican por qué y cómo la evidencia los respalda. También contiene compromisos normativos y metodológicos que especifican la idoneidad de las categorías, los criterios de adecuación justificadora y las formas de establecer que se han cumplido dichos criterios. La prioridad de una cuenta sobre sus componentes es epistémica, no histórica. No hay duda de que las personas llegan a aceptar una cuenta antes de aceptar los diversos elementos que la componen. Más bien, la afirmación es que, independientemente del orden en que se adquieran, los compromisos se justifican epistémicamente solo cuando se unen para constituir una explicación sostenible. Una explicación, en su conjunto, es sostenible a la luz de los compromisos antecedentes relevantes actuales. La aceptabilidad de las afirmaciones individuales, así como de los métodos y estándares, es derivada de su papel en una explicación sostenible. Tal vez un modelo lineal de justificación funcione para la creencia de que el gato está en la caja, pero la comprensión disciplinaria es holística. La afirmación de que los electrones tienen carga negativa se justifica solo en la medida en que lo sea la explicación científica que la incorpora.
Tal como se interpreta de manera estándar, el conocimiento es granular: viene en bits discretos. Los objetos del conocimiento son hechos individuales, expresados en proposiciones atómicas verdaderas o enunciados mediante sentencias declarativas atómicas. Rogelio sabe el hecho de que el autobús se detiene en la esquina; Luis sabe el hecho de que los chivos comen pasto. Se supone que cada grano de conocimiento se acumula sobre otros granos. Sin duda, un grano puede sostener a otro si se dispone con talento. Gran parte de nuestro conocimiento consiste en sentencias, creencias o proposiciones individuales: cosas que, aparentemente, poseen valor de verdad de forma aislada. El compromiso con la granularidad se manifiesta en la adhesión generalizada al veritismo jamesiano. De hecho, el objetivo jamesiano es ininteligible a menos que supongamos que el conocimiento viene en bits, decretos y unidades contables.
La comprensión disciplinaria del químico, del físico, del biólogo… no consiste en la agregación de declaraciones de hechos separados e independientemente asegurados; es una narrativa integrada y sistemáticamente organizada de un dominio de lo real. No hay verificación de sentencias aisladas ni justificación de creencias disciplinares mediante pruebas independientes, pues la mayoría de ellas carecen de consecuencias evaluables por separado. Independientemente de una explicación sobre la transferencia de calor, nada podría contar como evidencia a favor o en contra de la afirmación de que un proceso es adiabático. De forma análoga, sin una teoría etológica, nada podría contar como evidencia para sostener o refutar que cierto comportamiento de preparación expresa altruismo recíproco. En conjunto, los componentes de una explicación pueden generar implicaciones comprobables, tecnologías aún por nacer, teorías aún por surgir. Pero, al final, en la lógica que une estas sentencias no debería haber contradicción con las leyes de la naturaleza que ellas mismas articulan.
Como diría Quine, las afirmaciones científicas enfrentan el tribunal de la experiencia sensorial no individualmente, sino como un cuerpo de conocimiento teórico. Es decir, para Quine —en su crítica al “mito del lenguaje empírico” en Two Dogmas of Empiricism— ninguna proposición empírica se verifica o falsifica aisladamente, sino que lo hace como parte de una red teórica, o si se quiere, de una cuenta de granos finos. Pero el problema no es meramente epistémico. Algunas declaraciones científicas evidentemente carecen de valores de verdad de forma aislada. Si la individualización de los elementos a los que pretenden referirse —una especie, un retrovirus, un letón…— depende de proporcionar una cuenta o grupo de cuentas, puede que no haya ningún hecho independiente de la adecuación epistémica de esa cuenta o de los modos que la caracterizan.
A primera vista, parece una locura mantener un compromiso con una falsedad simplemente porque tiene otras características epistémicas atractivas. Parece el colmo de la irresponsabilidad cognitiva. Las acusaciones de deshonestidad intelectual, ilusión, falsa conciencia o algo peor saltan inmediatamente a la mente. Pero la ciencia transgrede rutinariamente el límite entre la verdad y la falsedad de los fenómenos que pretende representar. Suaviza las curvas e ignora los valores atípicos. Desarrolla y despliega modelos que pretenden representar. Somete a muestras de laboratorio, artificialmente diseñadas, a fuerzas que no se encuentran en la naturaleza. Recurre a experimentos mentales que desafían las leyes naturales. Incluso los mejores relatos científicos no son ciertos. No solo están plagados de anomalías y problemas pendientes, sino que, cuando tienen éxito, se basan en declaraciones, modelos e idealizaciones —similares a leyes— que se sabe que divergen de la verdad. El mundo contractual. El veritismo podría razonablemente no dejarse intimidar por la existencia de anomalías y problemas pendientes, ya que se interpretan fácilmente como defectos. El problema más grave viene con las leyes, modelos e idealizaciones que se reconoce que no son ciertas, pero que, sin embargo, son críticas —de hecho, parcialmente constitutivas— de la comprensión que ofrece la ciencia.
La ciencia progresa apoyándose en ficciones útiles. Considérese el problema que plantean los modelos. La ley de los gases ideales, pV=nRT, representa la relación entre presión, volumen y temperatura en un gas compuesto por moléculas esféricas, adimensionales, que no exhiben atracción mutua. No existe tal gas. De hecho, si nuestras teorías fundamentales son casi correctas, no podría haber tal gas: al estar sujetas a la gravedad, todas las moléculas se atraen entre sí. Ninguna molécula es esférica. Sin duda, hay modelos más refinados, como la ecuación de Van der Waals y la ecuación virial, que incorporan algunas de las características de los gases reales que el modelo del gas ideal omite. Pero también son idealizaciones: no representan con precisión ningún gas real. Sin embargo, estos modelos —que no son verdaderos de nada real— figuran en una comprensión genuina de cómo se comportan los gases reales.
Los experimentos mentales también deberían molestar al veritista. No son experimentos reales y, a menudo, ni siquiera son experimentos posibles. Einstein demostró la equivalencia entre la masa gravitacional y la masa inercial invitando a los científicos a comparar la experiencia de una persona que viaja en un ascensor en ausencia de un campo gravitacional, con su experiencia mientras está en reposo en presencia de un campo gravitatorio. Al carecer de señales externas, la persona no podía determinar en qué situación se encontraba. Para llevar a cabo ese experimento, sería necesario colocar a un sujeto inconsciente en un recinto sin ventanas, enviarlo a una región del espacio exterior distante de cualquier fuente significativa de gravedad, restaurarle la conciencia y preguntarle sobre sus experiencias. Eso es moral, práctico y físicamente inviable.
Evidentemente, también es innecesario. Los físicos toman el experimento mental por sí mismo para establecer la equivalencia. Lejos de ser defectos, los modelos, las idealizaciones y los experimentos mentales figuran ineliminablemente en la ciencia exitosa. Si la verdad es obligatoria, gran parte de nuestra mejor ciencia resulta ser epistemológicamente inaceptable y, quizás, intelectualmente deshonesta. Nuestro predicamento es el siguiente: podemos retener el requisito de la verdad e interpretar la ciencia como cognitivamente defectuosa o incluso no cognitiva, o podemos rechazar, revisar o relajar el requisito de la verdad y seguir siendo cognitivistas y devotos de la ciencia.
Suponemos que la ciencia proporciona una comprensión del orden natural. Con esto no queremos decir simplemente que una ciencia ideal proporcionaría tal comprensión, o que al final de la investigación la ciencia la proporcionará, sino que mucha ciencia real lo ha hecho y continúa haciéndolo. Supongamos, entonces, que gran parte de la ciencia real tiene una reputación cognitiva, de hecho, estimable. Por lo tanto, una epistemología adecuada debería explicar qué hace que una buena ciencia sea cognitivamente buena. Un compromiso demasiado estricto con la verdad se interpone en el camino. Tampoco es la ciencia la única víctima. En otras disciplinas como la filosofía, la historia, las ciencias políticas y la economía, así como en el discurso cotidiano, a menudo transmitimos información y avanzamos en la comprensión por medio de sentencias y otras representaciones que no son literalmente verdaderas. Una epistemología adecuada también debería tener en cuenta esto.
Justificando
Llegar al consenso, dice, que la aceptabilidad epistémica requiere algo así como una creencia verdadera, no fortuitamente justificada y confiable. La justificación —es decir, los requisitos de confiabilidad y creencia— involucra umbrales (grados de probabilidad de certeza). La conexión entre el hecho de que la creencia sea verdadera y que esté justificada o sea confiable no debería deberse a la suerte (el tipo incorrecto de suerte). Pero se supone que lo verdadero es un asunto absoluto. O el contenido de una creencia es verdadero, o no lo es.
Sugiero, sin embargo, que el llamado requisito de verdad sobre la aceptabilidad epistémica también implica un umbral. No estoy diciendo que la verdad en sí misma sea un concepto de umbral. Tal vez tal interpretación de la verdad facilitaría los tratamientos de la vaguedad, pero eso no es aquí nuestra mayor preocupación. Para nuestro propósito, la bivalencia clásica es aceptable: una oración, creencia o proposición es verdadera o es falsa. Nuestro punto es que la aceptabilidad epistémica no depende de si es verdad, sino de si es lo suficientemente verdadera, es decir, de si está lo suficientemente cerca de la verdad. Es cierto que, obviamente, esto tiene un umbral.
Esto plantea una serie de preguntas. Pero antes de abordarlas, me permito emitir un descargo de responsabilidad. No niego que la verdad (incondicional) sea un concepto inteligible o un ideal realizable. Entendemos fácilmente las instancias del esquema T:
“La nieve es blanca” es verdad = la nieve es blanca
“El poder corrompe” es verdad = el poder corrompe
“Los neutrinos tienen masa” es verdad = los neutrinos tienen masa
Y así sucesivamente. Mientras aludamos a las paradojas, una teoría de la verdad entre comillas es suficiente para mostrar que el criterio expresado en la convención T puede satisfacerse. Uno podría, por supuesto, querer más de una teoría de conceptos de verdad; esto es inobjetable, basta con cualquier teoría minimalista que sea verdadera. Somos muy conscientes no solo de eso:
“La nieve es blanca” es verdad = la nieve es blanca, pero también que “la nieve recién caída es blanca” es cierto.
La inteligibilidad y la replicabilidad de la verdad, por supuesto, no muestra nada sobre qué sentencias son verdaderas o qué verdades podemos descubrir. Sin embargo, hasta donde puedo mirar, nada sobre el concepto de verdad desacredita el veritismo (realismo centrado en lo verdadero y crudo, sin adornos heroicos). Dado que la verdad es un concepto intangible y autoconsistente, está abierto a la epistemología insistir en que solo las verdades son epistémicamente aceptables. Dado que la verdad es un objetivo realizable, tal postura no conduce inexorablemente al escepticismo. No niego que el veritismo sea una postura epistémica disponible. Pero creemos que es indebidamente limitante: impide que la epistemología dé cuenta de toda la gama de logros cognitivamente estimables.
Si la aceptación epistémica se interpreta como creencia y la aceptabilidad epistémica como conocimiento, el requisito de verdad parece razonable. Para los pensadores, no parece haber una brecha epistémicamente significativa entre creer que P y creer que P es verdadero. Normalmente, al enterarse de que su creencia de que P es falsa, un agente epistémico deja de creer que P. Además, considera epistémicamente obligatorio hacerlo. Uno debe creer solo lo que es verdad. Si no puede deshacerse de tal creencia, considera su fracaso como un defecto en su carácter epistémico, es decir, del método de acceso a la realidad, criterio de veracidad, limitaciones epistémicas y observación empírica. Tal vez una criatura sin una concepción de la verdad pueda albergar creencias. Un gato, que carece de la capacidad de ascenso semántico, podría creer que “hay un ratón en el revestimiento de madera” sin creer que “hay un ratón bajo el revestimiento de madera” fuera cierto.
En ese caso, la conexión entre creer que P y creer que P es verdadero no está exenta de excepciones. Pero, sea lo que sea que resulte válido para los gatos, no parece factible para ninguna criatura que tenga una concepción de la verdad creer que P sin creer que P es verdadero. Si la aceptación epistémica es una cuestión de creencia, la aceptación está estrechamente vinculada a la verdad. También lo está la afirmación. Aunque afirmar que P no es lo mismo que afirmar que P es verdadero, parece claro que uno no debe afirmar que P si está dispuesto a negar que P es verdadero o a suspender el juicio sobre si P es verdadero; tampoco se debe afirmar que P es verdadero si uno está dispuesto a negar que P o a suspender el juicio sobre si P. La afirmación o la creencia, entonces, parecen comprometidas con la verdad. El conocimiento comparte ese compromiso. Ya sea que el conocimiento sea equivalente o no a una creencia verdadera justificada o generada de manera confiable, una vez que alguien descubre la falsedad de algo que ella misma tomó por saber, retira su reclamo de conocimiento. Esta persona dice: “Pensé que lo sabía, pero estaba equivocada; no lo sabía”.
No sostengo que el compromiso con la verdad constituya el núcleo del significado de “creencia”, “afirmación” o “conocimiento”. Ese compromiso se entrelaza con nuestros puntos de vista, pero quizá no sea tan central. No afirmo que sea aceptable creer lo que es falso, ni que sea lingüísticamente válido afirmar lo que es falso. Más bien, sugiero que la aceptación epistémica no se reduce a la creencia ni siempre la presupone. Creer que P —o estar convencido de que P— es estar dispuesto, cuando uno atiende a los elementos a los que se refiere P, a sentir que es verdadero que P y falso que no-P. En cambio, aceptar que P es adoptar una política: considerar o postular que P, estar dispuesto a usar P como premisa, como base para la acción o como norma de inferencia en contextos cognitivos. Esto incluye también la disposición a ofrecer P como testimonio a otros. La aceptación, a diferencia de la creencia, no es disposición a representar, sino a actuar. Sin embargo, impongo dos restricciones: (1) solo nos ocupamos de casos donde los fines son cognitivos, dejando de lado los casos puramente prudenciales o caprichosos; (2) limitamos la aceptación a inferencias asertivas y a acciones no contraproducentes. Concedo que en un reductio se acepta temporalmente una premisa, pero esa aceptación es efímera y no sirve para nuestros fines.
La distinción entre creer y aceptar. Un agente epistémico que acepta una consideración P no solo está dispuesto a desplegarla en sus fines cognitivos, sino también en la acción. Alguien que, sobre la base del testimonio, creyera que el modus ponens es una regla válida de inferencia, pero no tuviera idea de cómo o cuándo aplicarla, no estaría en condiciones de aceptar el modus ponens. En mi uso, entonces, aceptar que P es estar dispuesto y ser capaz de tomar P como una premisa asertórica, norma epistémica o regla de inferencia en el razonamiento propio, o como base para la acción cuando los fines de uno son cognitivos. Rechazar esa P es aceptar que no-P. Retener esa P es no aceptar esa P y no aceptar esa no-P. La aceptación está orientada a la acción de una manera en que la convicción per se no lo está. En lo que sigue, continuaré usando el término “creencia” tal como se usa de manera estándar, para cubrir los casos en los que la convicción y la aceptación se alinean. El modus ponens expresa un paso válido de inferencia deductiva: si las premisas son verdaderas, la conclusión necesariamente también lo es.
Aunque hay una superposición considerable, la aceptación y la convicción pueden divergir. Uno puede estar convencido de proposiciones que en un contrato dado no acepta. Como, por ejemplo, aceptar “fumar tabaco causa cáncer”, y al mismo tiempo en una convivencia de amigos fumar. A menudo las personas aceptan cosas de las que no tiene convicción de ser congruentes en sus acciones. Aceptan proposiciones con fines de argumentar, como hipótesis de trabajo, y extraen sus consecuencias, lo aceptan como hipótesis, hacen inferencias y diseñan experimentos en laboratorio. Los experimentos arrojan datos que se esperaban, se convenció. Pero la aceptación fue interior e independiente de la convicción de dejar de fumar. La hipótesis de trabajo es una con la que los científicos diseñan experimentos, enmarcando y enfocando su investigación. Y se acepta solo mientras funcione, es decir, mientras sea epistémicamente productiva. Sostenemos que la aceptación en lugar de la convección es centrar en el acto cognitivo de conocer. El fumador tiene una convicción que reconoce que es injustificada, demasiado dependiente de ella, por fuerzas que no son racionales. Esto desde luego es desafortunado para su vida.
Aceptar que fumar causa cáncer no es un fallo del conocimiento. No hay defecto en esa verdad. Lo que ocurre es que la convicción está atada a factores biológicos: el placer inmediato que el cerebro obtiene de fumar puede pesar más que la verdad misma. Por eso, el paso de la creencia a la aceptación requiere un movimiento adicional: la creencia suele quedar ligada a la afirmación, mientras que la aceptación implica una disposición práctica. Muchas veces, al hablar, no estamos razonando ni justificando, sino profesando. Enunciar una creencia es, a menudo, profesar algo sin demostrarlo. De hecho, muchos profesores “profesan” el aprendizaje cuando en realidad solo trasladan información de un lugar a otro y evalúan la memoria irreflexiva. Sostengo que gran parte de nuestros resultados verbales —aquellos que consideramos cognitivamente responsables— se refieren más a la aceptación que a la creencia. Pero entonces, no podemos sostener cómodamente que tales resultados sean afirmaciones justificadas en sentido estricto. Regularmente, conversamos en términos de aceptación, no de creencia: aceptamos cosas que nunca hemos verificado como verdaderas.
El paso de la creencia a la aceptación exige un cambio adicional, pues la creencia está estrechamente ligada a la afirmación. Sostengo que gran parte de nuestros resultados verbales cognitivamente responsables se refieren más a la aceptación que a la creencia, y por ello no puede sostenerse cómodamente que tales resultados consistan en meras afirmaciones.
Pronunciar o inscribir seria y sinceramente algo con fines cognitivos —llamémoslo profesar— no se reduce al acto de afirmar. Regularmente razonamos verbalmente dentro de los parámetros de lo que aceptamos como convención de discusión, aunque no estemos íntimamente convencidos de ello. Así, los ateos profesan que “Dios existe y no es un engañador” cuando discuten la Sexta Meditación de Descartes; los nominalistas profesan la Teoría de las Formas al hablar de la línea dividida; los físicos profesan que “F=ma” cuando discuten movimientos lentos y de tamaño medio, aun sabiendo que las leyes de Newton han sido reemplazadas.
Algunos podrían objetar que lo que llamo profesar no es más que fingir. Desde ese punto de vista, al comentar la Sexta Meditación yo simplemente pretendería estar convencido por los argumentos de Descartes, o al hablar del movimiento de una bola de billar, pretendería que F=ma. Sin embargo, profesar no es lo mismo que fingir.
La paradoja de Moore lo muestra con claridad: enunciar “P, pero no creo que P” es absurdo, porque afirmar que P es presentar algo en lo que uno cree, mientras que añadir “no creo que P” es negar simultáneamente esa creencia. No es una contradicción lógica formal, sino una incongruencia pragmática que revela la imposibilidad de sostener seriamente esa posición. Y esta imposibilidad no se resuelve reduciendo el acto a mera simulación.
La estrecha conexión entre la convicción de que P y la convicción de que P es verdadera, explica por qué la convicción y la creencia son, en general, impermeables a la voluntad. Una convicción es verdadera solo si las cosas son como su contenido las presenta. La convicción “Está lloviendo” es cierta solo si, de hecho, llueve justo ahora. Pero si la convicción respondiera a la voluntad —es decir, si las ilusiones fueran un mecanismo eficaz para formar convicciones—, entonces, con querer o desear con suficiente fuerza, uno podría convencerse a sí mismo de que no lo está, incluso cuando existe amplia evidencia de lo contrario. El autoengaño es real, por lo que la impermeabilidad en cuestión no es absoluta. Sin embargo, el autoengaño es difícil de sostener si somos valientes con nosotros mismos, porque resulta arduo retener una convicción que vuela frente a la evidencia propia. En otras palabras, el cinismo es una conducta enfermiza. Desde Aristóteles hasta nuestros días, la mente humana se considera naturalmente orientada hacia la verdad como condición de su felicidad.
Normalmente, frente a la evidencia propia, nos mantenemos firmes en nuestras convicciones. Convencidos de una cosa u otra, el sesgo de creencia nos vuelve dogmáticos, es decir, cerrados a confirmar la verdad de manera regular. A veces, sin duda, nos convencemos a través de arduas investigaciones o de complejas cadenas de razones en las que inferimos que hay causalidad en su conexión. Pero incluso en estos casos, los frutos de nuestra experiencia parecen simplemente emerger del trabajo. No se presentan como una cuestión de elección analítica y reflexiva. Esto crea un enigma para la epistemología. Por un lado, no queremos afirmar que depende de un agente epistémico creer en una proposición para la que tiene —y reconoce que tiene— pruebas suficientes. Por otro lado, la epistemología es una disciplina normativa antes que una de formalidad matemática: está llamada a emitir pronunciamientos éticos sobre los agentes, es decir, sobre lo que deberían hacer en diversas circunstancias. Si somos pasivos con respecto a la creencia, entonces el “debería” parece impertinente. Si un pensador no puede evitar creer lo que hace, no sirve de nada decirle que debe creer algo diferente. Lo que él cree no depende de él.
Aquí, la distinción entre convicción y aceptación es útil. La convicción es pasiva. Mientras el pensador examina el paisaje árido, no puede evitar convencerse de que no está lloviendo, por mucho que desee que lo esté. Pero la aceptación implica agencia. Incluso si es impertinente criticar a los agentes epistémicos por convicciones que no pueden evitar albergar, no es impertinente criticarlos por las premisas y reglas de inferencia que aceptan. Porque la aceptación es voluntaria. Y es razonable preguntar si, o en qué medida, la aceptación de una premisa o regla dada promueve los objetivos cognitivos del agente. Al hacerlo, no necesita pensar que la proposición es cierta; solo necesita pensar que es lo suficientemente cierta para sus propósitos actuales. Identificar “a” con “b” no es sostener que “a” es idéntico a “b”; es sostener que, en las circunstancias dadas, no hace daño tratar “a” y “b” como idénticos.
Esto no quiere decir que cualquier consideración cuya aceptación haga que uno realice sus objetivos o aumente la probabilidad de hacerlo sea aceptable. Pero una consideración cuya integración fortalece la sostenibilidad que una explicación tiene constituye, por esa razón, un reclamo de aceptabilidad.
Falsedades felices
La comprensión a menudo se expresa y se transmite mediante símbolos, que son expresiones que intentan ser verdaderas. Muchos de ellos ni siquiera pretenden ser ciertos. Tales símbolos son falsedades epistémicas. El agente se siente feliz con ellas. No todos los modelos científicos son proposicionales. Además de las ecuaciones y los modelos verbales abductivos, la ciencia está plagada de diagramas donde las formas expresan funciones biológicas, como en el caso de las proteínas, y las simulaciones computacionales no son proposicionales; estrictamente, son algo plausible en su cercanía con la verdad. Pero, si se interpretan como representaciones reales de sus referentes, son claramente inexactas y falsas.
Entonces, a pesar de que el nombre es un poco inapropiado, para facilitar la exposición etiquetamos todos los modelos como falsedades (plausibles frente a la complejidad). Sostenemos que no podemos comprender las contribuciones cognitivas de la ciencia, o incluso nuestras explicaciones cotidianas de las cosas, si no damos cuenta de las funciones epistémicas que realizan tales símbolos.
Aquí hay algo familiar: cuando suavizamos las curvas de datos, normalmente se supone que cada punto de un gráfico representa una verdad determinada de forma independiente. Al interpolar y extrapolar más allá de estas verdades, esperamos discernir el patrón que instancian. Si la curva que dibujamos conecta los puntos de datos, esto es razonable. Pero los datos rara vez caen con precisión sobre la curva propuesta para explicarlos. A continuación, la curva revela un patrón que los datos no instancian.
Estrictamente, al parecer, el veritismo requiere aceptar los datos solo si estamos convencidos de que son verdaderos y conectar estas verdades para aducir verdades adicionales. En ese caso, la línea debe conectar todos los puntos de datos, sin importar cuán enrevesada resulte la curva. Las curvas complicadas enmascaran patrones y regularidades subyacentes. Sin embargo, parece cognitivamente deshonesto simplemente dejar que la esperanza triunfe sobre la experiencia. Seguramente necesitamos una mejor razón para eludir los datos e ignorar los valores atípicos que el mero hecho de que, de lo contrario, no obtendremos el tipo de teoría que queremos. Nadie, después de todo, prometió que los fenómenos se acomodarían complacientemente al tipo de explicación que deseamos.
A menudo tenemos muy buenas razones para pensar que los datos no deben, o al menos no necesitan, tomarse como completamente precisos. A veces reconocemos que nuestras mediciones son relativamente toscas en comparación con el nivel de precisión que buscamos. Entonces, cualquier curva que esté dentro de cierta desviación estándar de la evidencia cuenta como acomodada a la evidencia. A veces sospechamos que algún tipo de interferencia desvía nuestras mediciones; entonces, al trazar la curva, compensamos la supuesta interferencia. A veces confiamos en que las mediciones son precisas, pero pensamos que los fenómenos medidos son complejos, de los cuales solo nos interesan algunos aspectos. En ese caso, en el suavizado de curvas, por así decirlo, eliminamos los aspectos irrelevantes, interpretándolos como ruido.
Quizá, con un poco de agitación de manos, el veritismo podría aceptar tales razones para suavizar las curvas. A veces, sin embargo, no tenemos explicación para la divergencia de los datos con respecto a la curva suave. Pero podemos juzgar correctamente que lo que importa es la curva suave que indican los datos, no la curva irregular que realmente instancian. Cualquiera que sea la explicación, aceptamos la curva tomando su proximidad a los puntos de datos como nuestra justificación. Ignoramos los valores atípicos, pensando que hay algo inaceptable en ellos. Entendemos el fenómeno como la visualización del patrón que marca la curva. Por lo tanto, descartamos la desviación de los datos respecto de la curva suave como insignificante..
Ceteris paribus es una locución latina que significa “todo lo demás permaneciendo igual” o “siendo iguales las demás condiciones”. Muchas afirmaciones similares a leyes en la ciencia obtienen solo ceteris paribus. Por ejemplo, la ley muy familiar de la gravedad:
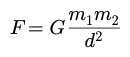
No es universalmente cierto, porque hay otras fuerzas en juego. La fuerza entre cuerpos cargados, por ejemplo, es el resultado de fuerzas eléctricas y gravitacionales. Sin embargo, no estamos inclinados a desechar la ley de la gravedad. La complicación que introduce la acusación solo muestra que la ley solo obtiene ceteris paribus, y cuando se acusan los cuerpos, ceteris no son paribus. Esto es noticia. “Ceteris paribus” en latín significa “otras cosas son iguales” pero no es obvio qué hace que la igualdad sea igual en un caso como este. Cuando una afirmación ceteris paribus es correcta, sus divergencias de la verdad no marcan la diferencia. Esto es plausible, pero no es agradable para el veritismo. Glosa “ceteris paribus” como “otras cosas son normales”, donde “normal” parece cobrar como “típico” o habitual de la inercia que nos invita a dejar de vivir con Eureka o lo sublime. Luego, una “ley ceteris paribus” establece lo que suele suceder. En ese caso, interpretar la ley de la gravedad como una ley ceteris paribus es sostener que, aunque hay excepciones, los cuerpos generalmente se atraen entre sí en proporción directa al producto de sus masas e inversamente al cuadrado de la distancia entre ellos. Una vez más, el veritismo podría manejar esto. Algunas leyes ni siquiera suelen ser válidas. La ley de la gravedad es una, ya que además de la gravedad, otras fuerzas, como la carga eléctrica, siempre afecta a los cuerpos que caen.
La generalidad de la ley también es valiosa por otra razón. A veces es útil representar primero un rayo de luz como conforme a la ley de Snell, y luego introducir correcciones para comandar los medios anisotrópicos. Si estuviéramos interesados solo en el camino de un rayo de luz en particular, un enfoque tan tortuoso no sería atractivo. Pero si estamos interesados en la refracción óptica en general, podría tener sentido comenzar con un caso prototípico y luego mostrar cómo perturba la anisotropía. Al retratar los casos anisotrópicos como perturbaciones, señalamos afinidades que las comparaciones directas no revelarían. El problema, entonces, es qué tipo de compresión queremos. Mostrar como una variedad de casos divergen del caso prototípico proporciona información valiosa sobre el fenómeno que nos interesa. Y lo que hace que el caso sea prototípico no es que generalmente se obtenga, sino que ejemplifica limpiamente las características que consideramos importantes.
Los hechos estilizados son parientes cercanos de las afirmaciones ceteris paribus. Son generalizaciones amplias, verdaderas en esencia, aunque quizás no en detalle. Desempeñan un papel importante en la economía, pues constituyen una explicación que los modelos económicos deben dar cuenta. Se supone que los modelos de crecimiento económico, por ejemplo, explican el hecho (estilizado) de que la tasa de ganancia es constante. El hecho sin adornos, por supuesto, es que las tasas de ganancia no son constantes. Todo tipo de factores no económicos, como la guerra, la peste, la sequía y las artimañas políticas, interfieren. Manifiestamente, los hechos estilizados no son hechos, por la sencilla razón de que no se obtienen. Podría parecer, entonces, que la economía se considera obligada a explicar por qué las falsedades conocidas son verdaderas. Esto no puede ser correcto. Más bien, la economía está comprometida con la opinión de que las afirmaciones que reconoce como hechos estilizados están en el vecindario correcto, y que su permanencia en ese vecindario es algo que los modelos económicos deben tener en cuenta.
Una pregunta crítica es qué significa estar en el vecindario correcto. Los modelos pueden mostrar que son buenas aproximaciones en todos los casos, o donde las desviaciones del ideal económico son clave, o donde los factores económicos dominan a los no económicos. O los modelos podrían permitirse alguna otra explicación de que a menudo tienen casi razón. Los modelos pueden inferir sobre lo que es realmente cierto, o, en cuanto a dónde, en qué grado y por qué, los hechos estilizados podrían perder información económica valiosa. Los hechos estilizados también figuran en otras ciencias. Sospechamos que, bajo esta descripción menos alarmante, también ocurren en las ciencias naturales. La caracterización estándar del péndulo, por ejemplo, nos parece un hecho estilizado de la física. El movimiento del péndulo que se supone que la física explica es un movimiento que ningún péndulo real exhibe. Lo que estos casos apuntan es lo siguiente: el hecho de que una descripción estrictamente falsa esté en el vecindario correcto a veces es parte integral de nuestra comprensión de un dominio.
En algunos contextos cognitivos aceptamos afirmaciones que no consideramos verdaderas. Pero tampoco aceptamos indiscriminadamente falsedades. La pregunta, entonces, es: ¿qué hace que una afirmación sea aceptable? Evidentemente, aceptar una afirmación no equivale a tomarla como verdadera, sino a asumir que su divergencia con respecto a la verdad, si la hay, es insignificante. Como dice Michael Strevens, esa divergencia no marca la diferencia. Strevens llama el “principio de negligencia” (the principle of disregard[37]): podemos ignorar ciertos desajustes entre afirmación y realidad siempre que no interfieran con la finalidad cognitiva. La divergencia no tiene por qué ser pequeña, pero, sea cual sea su magnitud, puede ser legítimamente ignorada. Aceptamos una afirmación, sugiero, cuando la consideramos lo suficientemente cierta para nuestros fines. El éxito de nuestros esfuerzos cognitivos indica que a menudo tenemos razón al hacerlo. Si es así, una afirmación resulta aceptable cuando su distancia respecto de la verdad es irrelevante. En ese caso, es bastante cierta.
Como hemos visto, las afirmaciones que son bastante verdaderas pueden divergir de la verdad de distintas maneras. Algunas lo hacen en aspectos irrelevantes; otras, en aspectos relevantes, pero solo de forma mínima. Hay afirmaciones que divergen mucho, aunque solo en raras ocasiones; y otras lo hacen en dimensiones que a sus usuarios no les interesan. También existen las que divergen a un nivel más fino de lo que resulta significativo para quienes las emplean. Finalmente, algunas se apartan radicalmente de la verdad, pero lo hacen de manera informativa y útil.
¿Cómo podría el veritista manejar tales divergencias? Una posibilidad es simplemente mantenerse firme. Podría insistir en que solo las verdades son epistémicamente aceptables. Entonces, si una explicación científica despliega interminablemente, modelos o idealizaciones que no son ciertas, esa explicación es inaceptable. Si se siente caritativo, el veritista podría conceder que tales dispositivos desempeñan un papel heurístico en la presentación o aplicación de la teoría. Pero insistiría en que, para que la explicación sea epistémicamente aceptable, deben ser eliminables sin pérdida de contenido cognitivo o justificación epistémica. Es probable que tal posición desacredite, de manera inverosímil, gran parte de nuestra mejor ciencia. No está claro hasta qué punto. Como hemos visto, el veritismo aparentemente puede acomodar algunas de las representaciones que he denominado falsedades felices al interpretarlas como aproximaciones. Podría, por ejemplo, acomodar la ley de la gravedad universal restringiéndola en lo relativo a la carga eléctrica.
Pero no todas las falsedades felices son siquiera aproximaciones correctas. La representación de Newton de la gravedad, aunque sea una buena aproximación, no garantiza que introduzca novedades en el acervo científico. Los delineadores mutuamente indiferentes detrás del velo de la ignorancia pueden ser epistémicamente aceptables o no. Algunas aproximaciones se aceptan simplemente porque son lo mejor que podemos hacer actualmente: expedientes temporales que esperamos —y quizá eventualmente personas como Einstein logren— reemplazar con verdades más sólidas. Tales aproximaciones pueden interpretarse, en términos de Sellars, como pagarés pendientes de liquidación: cuanto más nos acercamos a la verdad, más deuda se paga[38]. Sin embargo, no todas las aproximaciones tienen este carácter. Algunas incluso son preferibles a las verdades a las que se aproximan. Es posible, por ejemplo, derivar una ecuación diferencial parcial de segundo orden que describa exactamente el flujo del aire sobre el ala de un avión. La ecuación, al ser no lineal, no admite una solución analítica. Podemos formularla, pero nadie sabe cómo resolverla. Y eso resulta muy inconveniente.
Incorporar la verdad en la teoría detendría una línea de investigación, diciendo en efecto: aquí está la ecuación; es imposible de resolver. Los ingenieros de dinámica de fluidos prefieren una ecuación diferencial parcial de primer orden que se aproxima a la verdad, pero admite una solución analítica, es decir se deja espacio para “la construcción social (una en términos de la creación de verdad), el realismo, el pluralismo de tipos sociales, el contexto social, la dependencia contextual de la verdad social y la vaguedad social[39]”. La ecuación solucionable avanza en la comprensión al proporcionar una aproximación lo suficientemente cercana que genera valores numéricos capaces de servir como evidencia o como restricciones en investigaciones futuras. La aprobación, entonces, es más fructífera que la verdad. No hay esperanza de que la investigación futura remedie la situación si, como puede ser el caso, la ecuación de segundo orden no se puede resolver numéricamente, mientras que la de primer orden sí. Que la realidad nos obligue a tomar tal decisión puede ser decepcionante, pero, dadas las circunstancias, no parece intelectualmente deshonroso aceptar y preferir la ecuación manejable de primer orden. Un veritista podría argumentar que la aceptación de esta aproximación de primer orden es meramente práctica: es preferible simplemente porque es más útil. Esto puede ser así, pero la práctica es también cognitiva. Su objetivo es comprender el flujo turbulento. El valor práctico de la aproximación radica en que avanza la comprensión de un dominio. Por lo tanto, una falsedad feliz no siempre se acepta únicamente por defecto de la verdad. Tampoco su aceptación es simplemente la segunda mejor opción: puede hacer contribuciones cognitivas que exceden la verdad, al menos en el alcance del veritismo.
La alternativa final del veritista es decir que el uso de términos de éxito epistémico como “conocimiento” y “compresión” en casos que involucran falsedades felices en su uso de cortesía. Así como podríamos decir, tal vez un poco condescendientemente, que un niño pequeño tiene algún conocimiento de la fotosíntesis si piensa que la luz del sol es el alimento de la flor, el veritista podría decir, un poco condescendientemente, que Kepler tenía un entendimiento del movimiento planetario, aunque su afirmación de que la órbita del Tierra es elíptica es estrictamente falsa. Del mismo modo, el veritista podría decir que una teoría actualmente prometedora que tiene su parte de éxitos, pero algunas anomalías sobresalientes constituyen una comprensión de su tema. Al decirlo, en efecto está sacando un gravamen sobre el futuro.
1.7 Sesgos: es una cartografía del autoengaño moderno
El sesgo más difícil de admitir es el propio (sesgo de nuestro lado). Afecta a una amplia variedad de dominios de juicio y se manifiesta en personas de todos los grupos demográficos. Incluso pensadores expertos, altamente educados o de gran inteligencia, no están exentos de él. Su existencia ha sido ampliamente demostrada por la psicología cognitiva[40]; la psicología social y las ciencias políticas[41]; comportamiento económico[42]; estudios legales[43]; educación[44] y en razonamiento informal literario[45]. Se ha encontrado que el sesgo de nuestro lado ocurre en todas las etapas del procesamiento de la información. Es decir, los estudios han demostrado una tendencia hacia la búsqueda sesgada de evidencia, la asimilación sesgada de la información, la memoria distorsionada de los resultados y la generación también sesgada de nueva evidencia[46].
El sesgo de confirmación puede entenderse como una forma de estrategia de prueba positiva: se busca evidencia que se espera, dada la hipótesis focal en la mente del investigador. Siempre que el razonador considere adecuadamente la evidencia que no confirma su hipótesis, esta estrategia no es necesariamente no normativa.
Por otro lado, el sesgo de creencia (belief bias), identificado en paradigmas formales de razonamiento como las tareas silogísticas, consiste en la tendencia a juzgar la validez lógica de un argumento en función de si sus conclusiones coinciden con nuestras creencias previas, en lugar de evaluarlo según su estructura lógica. Formación de una creencia: es la contribución de la comprensión de la evaluación y el impacto persuasivo del texto argumentativo con objetivo de justificar una o más afirmaciones y persuadir a sus lectores a favor de una creencia o curso de acción particular. Como resultado, es un medio primario para la formación y el cambio de creencias. Los textos argumentativos varían en la estructura del argumento, es decir, el grado en que incluyen contraargumentos, y en el grado en que buscan explícitamente cambiar creencias previas[47].
El sesgo de mi lado (myside bias), presente en paradigmas de razonamiento informal —como las tareas de generación de argumentos y de evaluación de experimentos—, es la tendencia a razonar, buscar evidencia, evaluar argumentos y recordar información de manera sesgada a favor de nuestras creencias, actitudes o posiciones previas. A diferencia del sesgo de confirmación, que se refiere principalmente a la búsqueda selectiva de evidencia que respalde una hipótesis, el myside bias es más amplio y puede manifestarse incluso cuando no hay un incentivo explícito para defender una postura. Por ejemplo, una persona que cree firmemente que el cambio climático no es causado por la actividad humana puede evaluar con escepticismo los estudios científicos que lo confirman, pero aceptar sin cuestionamientos artículos de blogs o figuras afines que lo niegan, aunque carezcan de rigor[48].
A medida que el conocimiento se vuelve más accesible, también se vuelve más frágil frente a los filtros internos del sujeto. El pensamiento crítico no es solo una herramienta lógica, sino también una disciplina emocional: implica soportar la incomodidad de la evidencia que contradice nuestras convicciones más queridas.
Para reiterar, el término sesgo de confirmación se refiere al proceso cognitivo mediante el cual un pensador centra la evaluación y el análisis de la evidencia en torno a una hipótesis focal. No es necesariamente irracional —ni normativamente incorrecto— que un razonador muestre tal sesgo de confirmación, siempre y cuando esté dispuesto a procesar adecuadamente las implicaciones de la evidencia que no la confirma. Este punto ha sido reconocido desde hace mucho tiempo: mientras el razonador realice una actualización bayesiana apropiada al encontrarse con evidencia desconfirmatoria, buscar pruebas que sostengan su hipótesis focal no se considera inapropiado[49].
Para reiterar, el término sesgo de confirmación se refiere al proceso cognitivo mediante el cual un pensador centra la evaluación y el análisis de la evidencia en torno a una hipótesis focal. No es necesariamente irracional —ni normativamente incorrecto— que un razonador muestre tal sesgo de confirmación, siempre y cuando esté dispuesto a procesar adecuadamente las implicaciones de la evidencia que no la confirma. Este punto ha sido reconocido desde hace mucho tiempo: mientras el razonador realice una actualización bayesiana apropiada al encontrarse con evidencia desconfirmatoria, buscar pruebas que sostengan su hipótesis focal no se considera inapropiado.
Reputación cognitiva, es decir, la percepción social del valor, confiabilidad o competencia intelectual o mental de una persona, grupo o entidad, basada en sus capacidades cognitivas reales o atribuidas. Es decir, cómo se valora a alguien en términos de su inteligencia, razonamiento, juicio o conocimiento. Suponemos que la ciencia proporciona reputación cognitiva: una persona con la capacidad de comprensión del orden natural. Con esto no queremos decir simplemente que una ciencia ideal proporcione tal comprensión, o que al final de la investigación la ciencia ofrecerá una, sino que mucha ciencia real lo ha hecho y continúa haciéndolo. Suponemos entonces que gran parte de la ciencia real tiene reputación cognitiva del pensar fino, de hecho, estimable. Por lo tanto, una epistemología adecuada debería explicar qué hace que una buena ciencia sea cognitivamente elegante. Un compromiso desasido y estricto con la verdad se interpone en el camino. Tampoco es la ciencia la única víctima: también lo es la educación universitaria que no está mediada por la literatura, es decir, que solo transmite información y siente que avanza con la cantidad de contenido, y no en la capacidad de disertar explicaciones por medio de un discurso y narrativa que son, literalmente, estructuras elegantes de la verdadera ciencia. Una justicia epistemológica adecuada también debería tener en cuenta esto.
A diferencia del sesgo de confirmación, como lo hemos defendido, el término sesgo de creencias, utilizado principalmente en la literatura sobre razonamiento silogístico, tiende a connotar un error de razonamiento. Este sesgo ocurre cuando tenemos dificultades para evaluar conclusiones que entran en conflicto con lo que sabemos sobre el mundo[50].
1.8 Falsear datos
Falsear datos en los laboratorios, la forma más grave de mala conducta científica. La honestidad suele considerarse una virtud indiscutible. A diferencia de otros rasgos del carácter, como la humildad, rara vez se cuestiona si la honestidad es una excelencia moral que merece cultivarse. Sin embargo, ser honesto no se reduce simplemente a realizar acciones honestas.
Supongamos que alguien dice: “Rogelio hizo lo honesto al admitir que manipuló los datos del experimento en la asignatura de microbiología, dado que el equipo no fue calibrado y los reactivos muestran claros indicios de estar comprometidos en su integridad”. Es cierto que la honestidad puede dar lugar a acciones honestas, pero también es posible que una persona honesta pase largos períodos sin exhibir un comportamiento que revele esta cualidad. Del mismo modo, un historial de acciones honestas no basta para calificar a alguien como honesto. La honestidad, más que una serie de actos aislados es un rasgo estable del carácter, una disposición interna que define la estructura psicológica de una persona.
Tomemos de nuevo el caso de Rogelio: si admite haber manipulado los datos solo por temor a ser castigado, su acción puede ser honesta, pero él no necesariamente lo es. Aquí se revela una distinción clave: las acciones honestas no son lo mismo que la virtud de la honestidad. Para que una persona actúe desde la honestidad, su comportamiento debe emanar de un carácter honesto. En otras palabras, la honestidad genuina no es solo cuestión de conducta, sino de intención y disposición mental. Pensemos en la afirmación: “Rogelio llevó a cabo una evaluación exhaustiva y honesta de las evidencias del caso”. Aquí no se trata de una acción mental, sino de un proceso de pensamiento. Sin embargo, formar un juicio honesto en una ocasión específica no implica que Rogelio posea la virtud de la honestidad. Su carácter podría haber moldeado ese juicio, pero la virtud sigue siendo algo anterior y más profundo que un acto de pensamiento individual.
Entonces, ¿cómo identificamos la honestidad como un rasgo de carácter? Consideremos afirmaciones como estas:
Rogelio es una persona honesta.
He pasado suficiente tiempo con él para saber que es deshonesto y no quiere falsear datos.
Su carácter honesto realmente se destaca en su temple al aceptar el camino de la verdad científica; definitivamente, deberíamos premiarlo.
En estos casos, la atención se centra en la naturaleza de Rogelio como individuo, no solo en sus acciones específicas. Para que tenga la virtud de la honestidad, debe poseer una tendencia estable hacia la verdad, una disposición confiable a actuar con integridad científica (no ser un oportunista de asegurar que es honesto).
Así, si Rogelio tiene un carácter honesto, es probable que reflexione sobre la naturaleza del fraude en su experimento y reconozca que alterar datos equivale a hacer trampa en detrimento de su profesión de químico. Esta reflexión podría llevarlo a reportar las cifras correctas, pero el carácter honesto en sí mismo sigue siendo algo distinto de cualquier pensamiento o acción en particular. La virtud de la honestidad, en última instancia, es lo que subyace y da coherencia a estos actos como un argumento en la mente que justifica el progreso ético. Es decir, el argumento en la mente, juega un papel causal en su origen y, a su vez, esparce de la explicación causal de los mismos en forma de nuestro carácter ante la adversidad.
Además, los pensamientos que surgen de una disposición no se activarían todo el tiempo en todas las situaciones. Las excepciones podrían incluir ser pasivo o mirar la actividad científica como ridículamente frívola. Más bien, solo ciertas situaciones relevantes para este rasgo activan su disposición honesta en la actividad de reportar datos con integridad. Tratar de predecir con precisión cuándo sucederá esto depende de una serie de características específicas de su psicología, su identidad como estudiante de ciencias y su humildad intelectual para ser flexible al reconocer su debilidad ética.
Es posible que ni siquiera reconozca su falta de honestidad, pues en él no hay un juicio previo sobre la virtud del carácter científico ni sobre lo que debería ser su conducta. Presumiblemente, la mayor parte del tiempo tenemos una variedad de creencias y deseos subconscientes, así como corrientes inerciales que fluyen causalmente en nosotros por imitaciones de los otros, sin que nos demos cuenta. Los pensamientos que surgen de la virtud de la honestidad no serían una excepción.
Uniendo estas observaciones, aquí hay un punto de partida útil para pensar en la virtud de la honestidad en el mantenimiento de la integridad de los datos que se generan en un laboratorio.
Tesis: La virtud de la honestidad es una disposición psicológica que se forma como reflexión profunda. Cuando se desencadena en condiciones relevantes para la honestidad, puede causar de manera confiable la formación de pensamientos y sentimientos de tipo honesto, que en muchos casos pueden dar lugar posteriormente a acciones honestas.
1.8.1 Amor y honestidad
Naturalmente, los pensamientos y sentimientos honestos no siempre se traducen en acciones honestas. A veces, el entorno no coopera; por ejemplo, cuando a alguien se le impide hablar o actuar. En otras ocasiones, entran en juego consideraciones más importantes, como en casos en los que mentir o engañar podría prevenir un ataque de violencia.
Pero, en igualdad de condiciones, el desencadenamiento de una disposición honesta da lugar a pensamientos espontáneos, que a su vez generan una acción intencional. Hasta aquí, todo bien. Sin embargo, aunque la honestidad (H) puede ser útil para arrojar luz sobre el rasgo de carácter de una virtud, no esclarece completamente la naturaleza de la honestidad. ¿Por qué? Porque podríamos decir lo mismo de muchas otras virtudes. Consideremos la compasión: es una disposición psicológica que, cuando se activa en contextos relevantes, tiende a generar pensamientos y sentimientos compasivos, los cuales pueden conducir posteriormente a acciones compasivas. Las virtudes, en general, son disposiciones causales que suelen dar lugar a sus propios pensamientos y acciones relevantes. Lo mismo ocurre con los vicios.
¿Qué viene a la mente cuando piensas en ejemplos de honestidad? Una persona honesta es veraz en sus palabras y representa con precisión su visión del mundo ante los demás. Presenta los hechos con claridad, proporcionando la información necesaria para abordar adecuadamente el asunto en cuestión. Pero la honestidad va más allá. Una persona honesta también es confiable en el manejo de la propiedad ajena: respeta lo que pertenece a otros. Lo mismo puede decirse del cumplimiento de las reglas, como en el caso de jugar un juego de la manera correcta.
¿Y las promesas? Una persona honesta las hace con sinceridad, con la plena intención de cumplirlas si las circunstancias lo permiten (sin contrariar, por ejemplo, la segunda ley de la termodinámica). Y cuando llega el momento de la prueba en la realidad, honra su palabra, salvo que hayan surgido consideraciones de peso que justifiquen una excepción.
¿Qué implica mentir? La respuesta corta es que existe poco acuerdo entre los pensadores sobre cómo caracterizar rigurosamente la mentira. En lo que puede considerarse la narrativa tradicional, te digo una mentira si, y solo si:
1. te digo algo que creo falso, y
2. tengo la intención de engañar al decirlo.
El engaño aquí consiste en hacer que otros crean lo que decimos como verdadero. Así, por ejemplo, cuando un profesor pretende que el estudiante crea que habla con verdad, el efecto es que el estudiante acepta la afirmación. Cuando un estafador declara falsamente “soy garantía de decir verdad”, busca generar una actitud de confianza para aprovecharse de la vulnerabilidad de las personas. Este acto de teatro pretende hacerlo ver como máximo jurado de la verdad. Una mentira descarada sigue siendo mentira, incluso si quien la profiere asume el papel de actor: desde el principio todo relato necesita revisión a la luz de la evidencia, la literatura y el diseño experimental. El propósito de mentir, desde la perspectiva del estafador, se considera suficiente para justificar su engaño, con tal de evitar cualquier daño que altere sus privilegios. Surge aquí una pregunta interesante: ¿qué prueba que una persona sea un estafador en su decir? Quizá el hecho de que no soporte mirarse en el espejo y reconocer su deshonestidad, la imposibilidad de vivir con virtud[51].
Alguien que engaña a otros bajo la apariencia de ser confiable es, en esencia, deshonesto. No solo porque dice mentiras, sino porque retiene de manera intencional información importante, movido por razones que le otorgan la ilusión de controlar la narrativa de lo “real” y de sentirse importante al hacerlo[52].
Recibir un salario por un trabajo no realizado constituye un engaño. Quien, de manera consciente y voluntaria, manipula o transgrede las reglas legítimas, justas y equitativas que rigen la actividad laboral para obtener un beneficio indebido, no puede ser considerado honesto, sino corrupto. Se trata de un acto que distorsiona la confianza institucional, erosiona el sentido de justicia en el trabajo y vulnera el principio básico de reciprocidad que sostiene toda relación laboral[53]. Violó intencionalmente las reglas que rigen esta actividad y, con cinismo, alardea de su impunidad frente al acto, reafirmando su desdén por la justicia y la equidad.
Aquí el único punto es que hay muchos casos en los que hacer trampa es incompatible con la virtud de la honestidad, incluso si existen otros más complejos en los que tendremos que mirar más de cerca.
Romper promesas. Alguien que rompe promesas de manera consistente, razonablemente intencional y por razones morales insuficientes, no es alguien a quien llamaríamos honesto. El “intesionalmente” es importante, ya que uno puede romper una promesa sin querer, por ejemplo, olvidando o distrayéndose. Sin embargo, no me queda claro que todas esas rupturas involuntarias de promesas deban contar como ellas de honestidad. Al hacer una promesa, uno se asume una obligación moral. A menos que una sea liberado de la promesa, tiene al menos una obligación por lo tanto de hacer lo prometido. Romper una promesa, entonces, es violar centralmente esta obligación.
Con respecto a cada fracaso de la honestidad, hay una virtud correspondiente, veracidad frente a la mentira, franqueza frente al engaño, respeto frente a la apropiación, cumplimiento frente a la arbitrariedad, fidelidad frente a la traición:
Veracidad. La virtud de estar dispuesto a decir la verdad de manera confiable, por buenas razones morales.
Franqueza. La virtud de estar dispuesto a evitar el engaño de manera confiable, ofreciendo una presentación suficiente de los hechos relevantes por buenas razones morales.
Respeto por la propiedad. La virtud de estar dispuesto a respetar de manera confiable la propiedad de los demás por buenas razones morales.
Cumplimiento adecuado. La virtud de estar dispuesto a seguir de manera confiable las reglas relevantes en una situación de participación voluntaria, siempre que estas sean justas y apropiadas, y existan buenas razones morales para hacerlo.
Fidelidad a las promesas. La virtud de estar dispuesto a cumplir las promesas de manera confiable por buenas razones morales.
La imagen del viaje de Darwin es un recordatorio para recopilar datos con honestidad. La imagen de Don Quijote, que Cervantes nos regaló, quien se imaginó a sí mismo como un caballero y se enfrentó a molinos de viento, es un recordatorio para seguir soñando con actos de honestidad.
Los datos y la imaginación, en combinación adecuada, han sido claves en mi vida en la ciencia, la poesía y las matemáticas. Son recordatorios personales de algo que la mayoría de los científicos rara vez discuten o incluso admiten, a saber, que hay dos lados en el proceso de descubrimiento. Un lado del proceso es la confianza esperada en hipótesis, método, teoría, modelos, estadística, lógica y diseño experimental. El otro lado del proceso es mucho más misterioso e inescrutable. Este es el reino de la creatividad, la inspiración, la imaginación y, a menudo, la fuente intangible de toda nueva idea.
La honestidad es ese carácter que nos permite someter nuestras propias verdades a juicios rigurosos para contar con ellas como aliadas. El éxito de un estudiante de ciencias, diría, está en la intersección de estos dos reinos diferentes de la ciencia, junto con la humildad intelectual.
Por el arte de pensar la ciencia, me refiero a cómo encontrar y resolver acertijos científicos mientras te preparas para la parte divertida: los momentos Eureka en los que la naturaleza revela uno de sus secretos. Soy consciente de que estos momentos surgen del enfoque audaz de hacer ciencia con honestidad.
1.9 Diseño experimental
Como científicos, a menudo se busca crear teorías causales generalizables. Resulta que los experimentos, en los que se utiliza la asignación aleatoria para medir un efecto causal, son una herramienta sorprendentemente efectiva para ayudar en esta tarea. Pero, ¿cómo debemos hacer buenos experimentos? Algunos los modelan como un proceso que incluye la planeación y el diseño, la recopilación de datos, el análisis y la preparación de informes escritos. Sin embargo, en muchos casos aparece una trampa: la crisis de replicación experimental. La mayoría de los cursos escolares ponen un énfasis en el contenido de investigación —incluidas las teorías y los resultados discutidos desde diferentes enfoques—, pero es necesario un cambio: partir de preguntas como por qué hacemos experimentos y qué significa hacer una inferencia causal, hasta atender los pequeños detalles, como asegurarse de no perder los datos y de emplear la estadística adecuada.
En todo momento, una idea nos guiará: el propósito de los experimentos es estimar la magnitud de los efectos causales. Debemos transformar nuestras preguntas en preguntas causales. Seamos un poco más precisos sobre nuestra hipótesis: nuestra idea acerca del posible vínculo entre dos variables —causa y efecto—. La correlación observada en estudios de tipo observacional puede ilustrarnos, aunque sigue siendo desconcertante: podría existir correlación, pero no necesariamente una relación causal. Un factor de confusión puede explicar por completo la aparente relación. En tal caso, la correlación observada entre causa y efecto sería en realidad una estimación sesgada del efecto causal. La magnitud del sesgo introducido por los factores de confusión puede variar en diferentes escenarios: puede ser pequeña, o tan fuerte que nos lleve a concluir que existe una relación causal cuando en realidad no hay ninguna. Por esta razón decimos que correlación no implica causalidad. Una correlación entre dos variables puede ser consistente con una relación causal, pero también lo es con otras relaciones.
La gente a veces se pregunta si la causalidad implica correlación. La respuesta corta es: “no siempre”. Una relación causal entre dos variables suele implicar que estarán correlacionadas en los datos, pero no necesariamente. Por ejemplo, imagina que mides la velocidad de un coche y la presión sobre el pedal del acelerador. En general, presión y velocidad estarán correlacionadas, de acuerdo con la relación causal entre ambas. Pero ahora imagina que solo mides esas dos variables cuando alguien conduce cuesta arriba: en ese caso, la velocidad se mantendría constante mientras la presión aumenta, reflejando los intentos del conductor de sostener su ritmo. Por lo tanto, no habría correlación entre las dos variables en ese conjunto de datos, a pesar de que la relación causal se mantiene.
No se puede simplemente medir una correlación y saltar a conclusiones causales. La revolución de la ciencia de datos ha sido impulsada por el desarrollo de métodos estadísticos para razonar sobre las relaciones causales a partir de conjuntos de datos observacionales. Sin embargo, por muy interesantes que resulten esos métodos, solo son aplicables en circunstancias específicas. En contraste, el método experimental simple funciona como una vía para reducir el sesgo debido a los factores de confusión. Podemos decir que manteniendo constantes todas las variables excepto la que nos interesa en la manipulación experimental específica, es la lógica básica que sustenta el método experimental. La idea del experimento es mantener constante todo lo demás, para que podamos medir el efecto de la causa. Se intenta cortar el efecto de confusión.
Todo esto suena genial en teoría, podría pensar alguien, pero en realidad no podemos crear réplicas de mundo donde todo se mantenga constante. Entonces, ¿cómo realizamos experimentos en el mundo real? Si habláramos de experimentos para hornear un pastel, es fácil ver cómo podríamos mantener todos los ingredientes constantes y variar solo una cosa, como la temperatura de horneado. Hacerlo nos permitiría poner a prueba experimentalmente el efecto de la temperatura. Pero, ¿cómo podemos mantener algo constante cuando hablamos de personas, por ejemplo? Las personas no son pasteles. No hay dos iguales y, como todo padre sabe, ni siquiera los hijos educados del mismo modo resultan iguales.
La respuesta es la aleatorización. Si divides aleatoriamente una gran sala llena de personas en dos grupos, esos grupos, en promedio, tendrán un número similar de amigos. Del mismo modo, si eliges al azar quién en tu experimento recibe el tratamiento, encontrarás que los grupos de efecto y no efecto, en promedio, tendrán un número parecido de amigos. En otras palabras, a través de la aleatorización se controla el papel confuso de los factores. Pero lo más importante es que no solo se controla el efecto de las causas principales; también se equilibran, por ejemplo, el nivel educativo, la calidad del sueño y otros factores de confusión que podrían sesgar los resultados. Al dividir aleatoriamente un grupo grande de personas, los grupos, en promedio, serán iguales en todos los sentidos.
La aleatorización aparece entonces como un acto de humildad y pragmatismo: no se trata de fabricar mundos perfectos, sino de confiar en el azar como aliado metodológico. Es una paradoja: allí donde no podemos controlar la diversidad humana, el azar mismo se convierte en la herramienta de equilibrio. Lo que no podemos forzar a ser igual, podemos dejar que el azar lo distribuya. Y en ese gesto encontramos una manera imperfecta, pero poderosa, de acercarnos a la verdad.
Aquí está, entonces, nuestro diseño experimental simple: asignamos aleatoriamente a algunas personas a un grupo con la variable independiente y a otras a un grupo de control sin aplicar dicha causa. Luego medimos la variable dependiente —el efecto— en ambos grupos. La lógica básica de la aleatorización es que, si la causa genera el efecto, deberíamos observar más efecto, en promedio, en el grupo de la variable independiente.
La aleatorización es una herramienta poderosa, pero hay una advertencia: no siempre funciona. En promedio, la aleatorización asegurará que los grupos de análisis y medición de efectos sean iguales con respecto a los factores de confusión. Pero, así como al lanzar una moneda a veces puede salir “cara” nueve de cada diez veces, también puede ocurrir que uses la aleatorización y aun así aparezcan confusiones. Cuando aleatorizas, garantizas que, en promedio, todos los factores de confusión queden controlados. Por lo tanto, no habrá un sesgo sistemático en la estimación del efecto. Sin embargo, siempre existirá cierto ruido debido a la variación aleatoria. En resumen, la aleatorización es una forma notablemente simple y efectiva de mantener todo constante además de una variable manipulada. Al hacerlo, permite a los científicos experimentales hacer estimaciones imparciales de las relaciones causales. Es importante destacar que la aleatorización funciona tanto cuando se tiene el control de todos los aspectos del experimento —como al hornear un pastel—, como cuando no se tiene ese control, por ejemplo al realizar experimentos con personas.
Generalizabilidad es un problema de replicabilidad
Cuando hacemos preguntas sobre la realidad, es importante pensar en a quién estamos tratando de estudiar. ¿En partículas que están bajo diversas fuerzas? ¿En personas que viven en sociedades materialistas? Llamemos al grupo que estamos estudiando nuestra población de interés y a las personas que realmente participan en nuestro experimento nuestra muestra. El proceso de muestreo es lo que hacemos para reclutar personas en nuestro experimento. A veces, los investigadores toman muestras de una población, pero hacen una afirmación sobre otra población (generalmente más amplia). El desajuste de la muestra y la población, no siempre es un problema, pero muy a menudo las relaciones causales son diferentes para diferentes poblaciones.
Desafortunadamente, los científicos suelen asumir de manera generalizada que la investigación realizada sobre muestras específicas puede extrapolarse al resto del mundo, y a menudo no es así. Para resaltar este problema, Henrich, Heine y Norenzayan acuñaron el acrónimo WEIRD, que señala el error de hacer generalizaciones sobre toda la población a partir de experimentos en una muestra bastante inusual, porque los factores contextuales cambian.
Henrich y sus colegas argumentan que funciones psicológicas aparentemente fundamentales —como la percepción visual, la cognición espacial y el razonamiento social— difieren de manera significativa entre distintas poblaciones. Por lo tanto, cualquier generalización de un efecto estimado con una subpoblación WEIRD puede ser injustificada[54].
A principios de la década de 2000, los investigadores descubrieron que las intervenciones de gratitud —por ejemplo, escribir un breve ensayo sobre algo bueno que alguien hizo por ti— aumentaban la felicidad en estudios realizados en países occidentales. Con base en estos hallazgos, algunos psicólogos creyeron que las intervenciones de gratitud podrían incrementar la felicidad de todas las personas. Pero parece que estaban equivocados. Unos años más tarde, Layous (2013) realizó un experimento de gratitud en dos lugares de los Estados Unidos y en Corea del Sur[55]. Sorprendentemente, la intervención de gratitud disminuyó la felicidad en la muestra de Corea del Sur. Los investigadores atribuyeron este efecto negativo a los sentimientos de deuda que las personas en Corea del Sur experimentaron de manera más prominente al reflexionar sobre la gratitud. En este caso, podemos decir que los hallazgos obtenidos no pueden generalizarse a todas las personas del mundo.
Los problemas de generalización se extienden a todos los aspectos de un experimento, no solo a su muestra. Por ejemplo, incluso si nuestro experimento hipotético de intervención en efecto resultara en ganancias de felicidad, es posible que no estemos justificados para generalizar a diferentes formas de proporcionar dinero como factor de felicidad. Tal vez hubo algo especial en la cantidad que se dio o en la forma en que lo proporcionamos, lo cual condujo al efecto que observamos. Sin probar múltiples tipos de intervención diferentes[56], no podemos hacer una afirmación amplia en nuestro ejemplo, sobre la felicidad. Este problema tiene consecuencias tanto para nuestros análisis estadísticos como para nuestros diseños experimentales[57].
Las cuestiones de generalización son omnipresentes, pero el primer paso es simplemente reconocerlas y razonar sobre ellas. Quizás todos los reportes de investigación deberían declarar la restricción de generalidad, donde los investigadores discutan si esperan que sus hallazgos se generalicen a través de diferentes muestras, estímulos experimentales, procedimientos y características históricas o temporales. Este tipo de declaraciones al menos recordaría a los investigadores que deben ser humildes: los experimentos son una herramienta poderosa para comprender cómo funciona el mundo, pero hay límites a lo que cualquier experimento individual puede enseñarnos. Así lo expresan Simons, Shoda y Lindsay: “A menudo, no es posible determinar definitivamente si un intento de replicación se considera "directo" o no, debido a la flexibilidad en la interpretación de las diferencias de procedimiento. Especificar restricciones de generalidad en los artículos originales puede eliminar la ambigüedad de antemano, lo que conduce a una ciencia más acumulativa[58]”.
Teorías
Cuando haces un experimento, a veces solo quieres ver qué sucede, como un niño derribando una torre hecha de bloques de madera. Y a veces deseas conocer la respuesta a una pregunta aplicada específica, como: “¿dar un texto a los estudiantes y medir el desempeño de su capacidad de síntesis?”. Pero, más a menudo, nuestro objetivo es crear teorías que nos ayuden a explicar, predecir y determinar lo posible (contrafactual) en nuevas observaciones.
¿Qué es una teoría? Argumentaremos aquí que debemos pensar en las teorías como conjuntos de relaciones propuestas entre constructos: variables que creemos que juegan un papel causal en la determinación del comportamiento de lo real. En esta concepción de las teorías, el papel de la causalidad es central: las teorías son conjeturas sobre la estructura causal y sobre las relaciones causales entre mente y mundo. Esta definición involucra al observador y sus sesgos. La teoría y los marcos de referencia son amplios conjuntos de ideas que guían la investigación, aunque no siempre hacen contacto específico con observaciones empíricas particulares.
Los constructos son las variables que queremos que describa nuestra teoría, como el caso de “dinero” y “felicidad”. A primera vista, puede parecer extraño que necesitemos un concepto específico para estas variables, pero debemos construirlo: de ello depende justificar el constructo. Por ejemplo, para encontrar la relación entre dinero y felicidad, tendremos que hallar una manera de que el concepto permita hacer mediciones. Digamos que solo pedimos a la gente que responda: “¿qué tan feliz es usted?”, otorgando una puntuación en una escala de 1 (miserable) a 10 (sublime).
Ahora supongamos que alguien en el estudio informa un 8 en esta escala. ¿Es esto realmente lo feliz que es? ¿Qué pasaría si no se concentrara mucho en la calificación, o si pensara que el investigador quería que respondiera con mayor felicidad? ¿Qué sucede si, en sus interacciones con familiares y amigos, actúa mucho menos feliz?
Esto revela un dilema: las calificaciones de autorreportes que recopilamos son solo un reflejo parcial de una construcción latente, la felicidad. El constructo es latente porque nunca podemos verlo directamente, aunque creemos que tiene una influencia causal en la medida: las personas más felices deberían, en promedio, dar puntuaciones más altas. Pero muchos otros factores pueden provocar ruido o sesgo en la medición, de modo que no debemos confundir esas calificaciones con el constructo mismo.
Un punto crucial de la investigación científica: nuestras herramientas conceptuales son mediaciones, no espejos fieles de la realidad. El conocimiento no es solo acumulación de datos, sino también construcción de marcos que dan sentido. Una teoría, entonces, no es un mapa exacto del mundo, sino un artefacto humano que nos permite orientarnos en él. Reconocer la distancia entre constructo y realidad no debilita a la ciencia: la hace más humilde, más consciente de sus límites y, por tanto, más verdadera en su intento.
La pregunta particular “¿qué tan feliz eres?” es una forma de pasar de la construcción general a una medida específica. Este proceso de transformar una construcción abstracta en una instanciación concreta, que pueda ser medida o manipulada, se llama operacionalización. La felicidad puede ponerse en práctica de muchas maneras: por ejemplo, a través del análisis del uso de lenguaje positivo en un ensayo personal, mediante las calificaciones otorgadas por amigos, familiares o incluso por un médico. Estas decisiones sobre cómo operacionalizar un constructo con una medida particular son complejas y tienen consecuencias importantes. Cada operacionalización puede ser apropiada para un estudio específico, pero requiere justificación y argumentos que permitan conectarla con otras posibles medidas.
Proponer un constructo particular es una parte muy importante de la elaboración de una teoría. Por ejemplo, un investigador podría preocuparse de que los autorreportes de la felicidad son muy diferentes al bienestar observado por las personas que rodean a alguien, y afirmar que la felicidad no es una construcción única, sino más bien un grupo de construcciones distintas. Este investigador se sorprendería al saber que los autorreportes de felicidad se relacionan muy bien con las percepciones de los demás sobre el bienestar de una persona. Que el autorreporte y la percepción de los otros coincidan, al menos en parte, revela que incluso en lo más subjetivo hay puentes hacia lo intersubjetivo, hacia lo compartido.
Una síntesis hasta aquí, es la tensión entre lo que la mente construye y lo que el mundo ofrece como resistencia. Al recordar que toda teoría es un artefacto humano: la ciencia no es un oráculo, sino un lenguaje que aproxima, organiza y propone. Constructo operacionalizado es especialmente potente, nos muestra cómo lo humano o lo natural se vuelve medible a través de decisiones metodológicas que nunca son neutras.
Incluso las variables externas, aparentemente no psicológicas, como masa o carga eléctrica, no tienen efectos directos con las personas, sino que operan a través de constructos. Finalmente, un constructo puede ser operacionalizado a través de una manipulación conceptual de la relación causa-efecto (dinero-felicidad). Al tomar un conjunto de constructos abstractos que le interesan al investigador y formaran parte del diseño experimental específico con una manipulación de controles, una medida de tamaño de muestra que pone a prueba su teoría causal.
La relación entre constructos
Los constructos adquieren su significado en parte a través de sus propias definiciones y operacionalizaciones, pero también en parte de sus relaciones causales con otros constructos. Las hipótesis de relaciones causales entre constructos forman una red nomológica: un conjunto de propuestas sobre cómo las diferentes entidades están conectadas entre sí. La parte complicada es que los constructos clave nunca se observan directamente. Por lo tanto, los investigadores solo pueden ponderarlos midiéndolos a través de su operacionalización específica. Una forma poética de pensarlo es que el sistema teórico de constructos “flota, por así decirlo, por encima del plano de observaciones y está anclado a él por reglas de interpretación”. Entonces, incluso si una teoría postula que dos constructos —causa y efecto— están directamente relacionados, lo mejor que puede hacer el investigador es manipular una operación y medir otra. Si esta manipulación no produce ningún efecto, es posible que estemos equivocados y, por ejemplo, que el dinero no cause felicidad. Pero también es posible que la operacionalización empleada sea pobre.
Aquí hay una forma ligeramente diferente de pensar una teoría. Una teoría proporciona una comprensión de datos potencialmente complejos al condensarlos en un conjunto mucho más pequeño de factores generales. Por ejemplo, si tienes una secuencia larga de números —digamos 2, 6, 16, 32, 64, 128, 256…— la expresión corta 2^n funciona como una compresión de esa secuencia: nos dice qué números pertenecen y cuáles no. De la misma manera, una teoría puede comprimir un gran conjunto de observaciones (quizá los datos de muchos experimentos) en un pequeño conjunto de relaciones entre constructos. Ahora bien, si tus datos son ruidosos —es decir, incluyen desviaciones decimales como 2.4, 6.1, 31.8, 64.7, 128.01, 255.8…— entonces la teoría no será una representación perfecta de los datos. Sin embargo, seguirá siendo útil dentro del margen de incertidumbre práctico.
En particular, tener una teoría le permite explicar los datos observados y predecir nuevos datos. Ambas son cualidades valiosas en una teoría. En el ejemplo de la relación entre dinero y felicidad, si hubiera causalidad, podríamos usarla para explicar observaciones como los niveles más altos de felicidad entre personas ricas. También podríamos hacer predicciones sobre los efectos de políticas como otorgar un ingreso básico universal en la felicidad general. La explicación es una característica importante de las buenas teorías, pero también es fácil engañarse a sí mismo usando una teoría vaga para explicar un hallazgo después del hecho. Por lo tanto, la mejor prueba de una teoría suele ser una nueva predicción. ¿A qué o a quién se aplica esta teoría? Es una pregunta importante que debe hacerse sobre cualquier marco causal propuesto.
En psicología, muy pocas causalidades que llevan la etiqueta de “teorías” describen relaciones causales que vinculan constructos claramente definidos y operacionalizados. Un ejemplo de algo que se llama teoría pero que no cumple con los componentes descritos anteriormente es la teoría de sistemas ecológicos (EST) de Bronfenbrenner (1992[59]). La tesis clave de esta propuesta es que el desarrollo de los niños ocurre en un conjunto de contextos anidados que se afectan entre sí y, a su vez, afectan al niño. Esta teoría ha sido inmensamente influyente; sin embargo, si se lee como una teoría causal, casi no tiene sentido: prácticamente todo se conecta con todo en ambas direcciones, y los constructos no están operacionalizados. Así, resulta muy difícil averiguar qué tipo de predicciones realiza.
La teoría de sistemas ecológicos (EST) no es realmente una teoría en el sentido que defendemos, y lo mismo ocurre con muchas otras ideas muy interesantes en psicología. No es un conjunto de relaciones causales entre constructos que permitan predicciones específicas sobre observaciones futuras. La teoría de sistemas ecológicos es, en cambio, un amplio conjunto de ideas sobre qué tipo de teorías tienen más probabilidad de explicar fenómenos específicos.
Por ejemplo, nos ayuda a recordar que es probable que el comportamiento de un niño esté influenciado por una amplia gama de factores, de modo que ninguna teoría individual puede centrarse solo en un factor particular y esperar proporcionar una explicación completa. En este sentido, EST es un marco: guía e inspira teorías específicas, en el sentido que hemos discutido aquí, es decir, un conjunto de relaciones causales entre constructos, sin ser una teoría en sí misma.
Los marcos como EST suelen ser increíblemente importantes. También pueden marcar una gran diferencia en la práctica. EST apoya un modelo en el trabajo social en el que las necesidades de los niños se consideran no solo como la expresión de problemas específicos de desarrollo interno, sino también como derivadas de un conjunto de factores contextuales superpuestos. Concretamente, es más probable que un psicólogo examine los entornos (familiares, laborales y escolares) al analizar la situación de un niño a través de una lente EST. Una teoría, con su rigor causal y capacidad predictiva, ofrece precisión, pero puede volverse estrecha; un marco, en cambio, abre el horizonte y nos recuerda que la realidad es siempre más amplia que las categorías con las que intentamos entenderla. El valor de EST, no es tanto predecir con exactitud, sino orientar la mirada hacia la complejidad: que el niño no es un ente aislado, sino un nodo en una red de influencias contextuales. Esa conciencia evita reduccionismos y nos invita a la humildad: la ciencia psicológica no siempre puede dar respuestas cerradas, pero sí puede ofrecer lentes más justas para comprender lo humano.
Hay un continuo entre teorías específicas, con precisión, y marcos amplios. Algunas teorías proponen constructos interconectados, pero no especifican cómo deben ser operacionalizados. Por ello, cuando leas un artículo científico que afirma proponer una “teoría”, es una buena idea preguntarse si describe relaciones específicas entre constructos ya operacionalizados. Si no es así, puede ser más un marco que una teoría. Resalta una distinción fundamental en el trabajo intelectual: no confundir amplitud con rigor. Una teoría sin operacionalización corre el riesgo de quedarse en metáfora elegante, mientras que un marco demasiado cerrado puede sofocar la imaginación. El continuo que mencionas recuerda que la ciencia no avanza solo con predicciones exactas, sino también con orientaciones que guían las preguntas. El punto está en aprender a leer con espíritu crítico: reconocer cuándo estamos frente a una estructura explicativa y cuándo ante un conjunto inspirador de intuiciones.
El desarrollo de la teoría no se trata solo de un condimento para el conocimiento, sino que tiene implicaciones directas en las tecnologías y políticas construidas a partir de esas teorías. Un ejemplo proviene de la infame teoría de Edward Clarke sobre los supuestos efectos nocivos de la educación en las mujeres[60]. Clarke postuló que los procesos cognitivos y reproductivos se basaban en una misma reserva fija de energía. Según su argumento, los procesos reproductivos de las mujeres requerían más energía que los de los hombres, por lo que dedicar demasiada energía a tareas cognitivas, como la educación, agotaba la energía necesaria para mantener un sistema reproductivo saludable. Basándose en estudios de casos, Clarke sugirió que la educación estaba causando que las mujeres se enfermaran, experimentaran problemas de fertilidad y dieran a luz a niños más débiles. Por lo tanto, concluyó que los varones debían estudiar y trabajar a la manera de los varones, y las mujeres a la manera de las mujeres.
El trabajo de Clarke es un ejemplo escalofriante de las implicaciones de una teoría poco desarrollada. En este escenario, Clarke no tenía instrumentos que le permitieran medir sus constructos ni experimentos que pusieran a prueba las conexiones causales entre ellos. En cambio, simplemente destacó estudios de casos que coincidían con su idea. Sus planteamientos finalmente perdieron popularidad, especialmente cuando fueron sometidos a experimentos rigurosos. Sin embargo, los argumentos de Clarke se utilizaron para intentar disuadir a las mujeres de acceder a la educación superior y obstaculizaron durante un tiempo la configuración de la política educativa.
1.10 Conocimiento y justificación
La justificación doxástica es un concepto en epistemología que se refiere a la justificación de una creencia (en lugar de un conocimiento en sentido fuerte). La idea es que una creencia está justificada doxásticamente si la persona tiene razones o evidencia suficientes para sostenerla como verdadera, independientemente de si realmente es verdadera.
En otras palabras:
Creencia: algo que uno acepta como verdadero.
Justificación doxástica: estar razonablemente respaldado para mantener esa creencia, aunque pueda ser falsa.
Se contrasta con la justificación epistémica para conocimiento, donde se requiere verdad y otros criterios más estrictos.
Nota: Para más detalle en esta discusión por favor de apoyarse en curso en línea: Lógica II: Proposicional: https://libertadacademica.com/Bachillerato2021Logica2/pages/Logica2.html
La noción de conocimiento se centra, en gran medida, en la justificación de nuestras creencias. Una cuestión central en epistemología es si esta justificación debe ser internalista o si un enfoque externalista puede explicar mejor el conocimiento. El externalismo sostiene que el conocimiento puede depender de relaciones naturales entre el sujeto y su entorno, sin que el sujeto necesariamente tenga acceso consciente a todos los elementos que justifican su creencia. En otras palabras, es posible creer justificadamente algo sin saber que es verdad, siempre que la creencia esté conectada de manera adecuada con la realidad. Para los externalistas, la justificación puede ser un componente del conocimiento, pero no necesariamente requiere que el sujeto tenga un acceso introspectivo completo a esa justificación. Por el contrario, los internalistas defienden que la justificación depende completamente de lo que es accesible al sujeto desde su propia perspectiva. Algunos incluso pueden negar que el conocimiento requiera justificación en un sentido internalista estricto.
Imagina que ves un árbol frente a ti. Rogelio la cree: “Hay un árbol frente a mí”.
Un internalista diría: para que realmente sepas esto, debes tener acceso a las razones que te justifican. Es decir, debes poder reflexionar y decir: “Veo un árbol, puedo percibir su forma, altura y hojas; por eso sé que hay un árbol”. La justificación depende de tu conocimiento interno de por qué crees algo. Un externalista, en cambio, se centra en la conexión entre tu creencia y el mundo. Mientras tu percepción sea confiable y funcione correctamente para formar creencias verdaderas, tú sabes que hay un árbol, aunque no puedas explicar todos los detalles que justifican tu creencia. Es decir, no necesitas reflexionar sobre tu proceso; basta que tu mente esté conectada de manera adecuada con la realidad.
Diferencia clave:
Internalismo → la justificación debe ser accesible a tu mente.
Externalismo → basta que tu creencia esté conectada de forma correcta con la realidad, incluso si no puedes explicarlo.
Así, el externalismo permite que tengas conocimiento incluso cuando no sabes exactamente por qué sabes, mientras que el internalismo exige que puedas justificarlo internamente.
Considere dos preguntas
Q1: ¿Es posible tener conocimiento sin justificación?
Q2: ¿Es posible tener justificación sin conocimiento?
Para responder correctamente a estas preguntas, debemos distinguir entre tres tipos de atribuciones de justificación:
Justificación personal: S está justificado al creer P.
Justificación doxástica: La creencia de S de que P está justificada / S cree justificada P.
Justificación proposicional: S tiene una justificación para creer P / hay una justificación para que S crea P.
Las justificaciones personales nos dicen algo sobre el creyente: si está justificado para creer. Una adscripción de justificación doxástica, en cambio, nos dice algo sobre una creencia: si dicha creencia se sostiene justificadamente. Por su parte, una adscripción de justificación proposicional nos dice algo sobre una proposición: si hay suficiente justificación como para que alguien pueda creerla. Que yo sepa, no existe una práctica establecida que trate la justificación personal y la doxástica como intercambiables. Considerarlas equivalentes constituye un error, aunque, como suele ocurrir, un error relativamente inofensivo. Lo que más nos interesa no es tanto la noción de una creencia que está justificada, sino cómo una persona se siente justificada al sostener una proposición. La pregunta decisiva es: ¿cuándo está justificado que una persona crea algo de tal manera que se aplique la justificación? Una persona está justificada para creer en una proposición cuando no puede esperarse razonablemente más de ella en su esfuerzo por determinar si esa proposición es verdadera. Sin embargo, aquí se revela un punto clave: puede haber casos en los que no se pueda exigir razonablemente más de alguien, en su calidad de buscador de la verdad, y aun así la proposición en cuestión resulte ser falsa.
Esta distinción entre justificación personal y doxástica es importante para nuestros propósitos por dos razones. Primero, considero que algunos críticos tenían razón al afirmar que sus ejemplos no eran casos de justificación doxástica sin conocimiento, sino más bien de justificación personal sin conocimiento. De este modo, una persona podría estar justificada al creer en alguna proposición sin saber que dicha proposición es verdadera. En segundo lugar, los externalistas pueden acomodar ciertas intuiciones internalistas al conceder que la justificación personal es, en efecto, una noción internalista, al tiempo que insisten en que la justificación doxástica no lo es.
La distinción entre justificación personal y doxástica es análoga a la distinción acto/agente en ética. Una persona puede ser completamente excusada por haber actuado mal cuando ignora, sin culpa, algún hecho relevante o cuando actúa conforme a una creencia errónea. En tales casos, saber que es moralmente íntegra y que sus acciones reflejan bien en ella no implica necesariamente que dichas acciones se ajustaran a las demandas de la ética. Del mismo modo, una acción puede ajustarse a las exigencias éticas incluso si se realiza por motivos egoístas y, por lo tanto, no constituye un mérito para el agente ni un signo de buen carácter. En general, resulta útil pensar las justificaciones como defensas. Para comprender adecuadamente la justificación personal, doxástica y proposicional, debemos entender lo que implica defender a las personas, a las creencias particulares y a las creencias prospectivas. Defender a una persona que cree P consiste en mostrar que la manera en que forma sus creencias la presenta como epistémicamente responsable. Defender una creencia, en cambio, es mostrar que esa creencia se ajusta a las normas que gobiernan la formación y sostenimiento de las creencias.
¿Cómo se relacionan estos diferentes tipos de atribución de justificación? Parece plausible que uno pueda creer justificadamente en P solo si tiene una justificación para creer en P y esa justificación juega algún papel en la explicación de por qué cree lo que cree. Ciertamente resulta contradictorio afirmar que una creencia de culpabilidad está perfectamente justificada mientras se insiste en que no hay justificación alguna para que alguien crea que una persona es culpable.
El punto de vista estándar sostiene que la justificación doxástica implica tanto una justificación proposicional como una base adecuada. Para creer justificadamente en P, se requiere tener una justificación para creer en P, y que esa justificación sea la razón por la cual se sostiene la creencia. Si bien la justificación doxástica es suficiente para la justificación personal, lo contrario no es cierto. Puede haber suficiente justificación para que creas cosas que no crees; sin embargo, no puedes creer justificadamente aquello que no crees.
Algunos sostienen que las adscripciones de justificación personal y doxástica son lógicamente equivalentes. Creo que esto es un error. Aunque las creencias no pueden justificarse si una persona no está justificada para sostenerlas, es posible que alguien esté justificado para creer algo incluso si sus creencias particulares no estaban justificadas. Una persona está justificada en sus creencias si puede ser considerada responsable de ellas y no se le puede culpar por ningún incumplimiento del deber epistémico.
Es decir, una persona está justificada en sus creencias si persigue sus fines epistémicos de manera responsable y puede asumir racionalmente que ha cumplido con sus obligaciones epistémicas. Una creencia, en cambio, está justificada si se sostiene de manera permisible. Puedes ser excusado si no cumples con tus obligaciones epistémicas, pero no puedes dejar de cumplirlas justificadamente si te nombras académico o científico. Mientras que la justificación personal no requiere más que una excusa (a veces teñida del cinismo de intentar por todos los medios ocultar el egoísmo y la impunidad), la justificación doxástica exige permisibilidad.
Si Q1 tiene que ver con la justificación personal, la pregunta es si se le puede culpar por creer lo que sabe. Si Sabres que tus creencias son verdaderas, no se te puede culpar con razón por una violación del deber epistémico de evaluar sus credenciales de verdad. No sería razonable que yo dijera que usted fue irresponsable o irrazonable al creer que había admitido que sabía tenía razón. Si Q1 es una pregunta sobre la justificación doxástica, la pregunta es si su obligación puede ser abstenerse de creer lo que sabe que es verdad. Si admite que una persona conoce P, no puede decir que esta persona no estaba en condiciones de juzgar correctamente si P era cierto. El conocimiento es suficiente para la justificación doxástica si sus creencias justificadas son creencias permisibles. Dado que la justificación doxástica requiere justificación proposicional, el conocimiento es suficiente para la justificación proposicional.
Obligaciones epistemológicas son deberes o responsabilidades que tenemos respecto a nuestras creencias y conocimientos. Es decir, no se refieren a obligaciones morales hacia otros, sino a lo que razonablemente debemos hacer para formar, mantener o revisar nuestras creencias de manera correcta desde un punto de vista epistemológico.
Podemos entenderlas de la siguiente manera:
Buscar evidencia suficiente:
Tenemos la obligación de fundamentar nuestras creencias con evidencia adecuada antes de aceptarlas como verdaderas. No es suficiente con intuiciones o prejuicios.
Evitar la credulidad indebida:
No debemos aceptar creencias sin cuestionarlas, especialmente si hay motivos para dudar o si la evidencia es débil.
Revisar y actualizar creencias:
Cuando llega nueva evidencia o información relevante, tenemos la obligación epistemológica de reconsiderar nuestras creencias y ajustarlas si es necesario.
Coherencia interna:
Debemos procurar que nuestras creencias no se contradigan entre sí. Mantener un sistema de creencias consistente es parte de actuar responsablemente epistemológicamente.
Justificación doxástica:
Antes mencionada nuestra creencia deben estar respaldadas por razones suficientes, aunque no se requiera que sean absolutamente verdaderas.
Evitar sesgos y distorsiones:
Ser conscientes de sesgos cognitivos, prejuicios o influencias externas que puedan nublar el juicio es parte de cumplir con las obligaciones epistemológicas.
En síntesis, tener obligaciones epistemológicas significa formar y sostener creencias de manera responsable, crítica y racional, reconociendo los límites de nuestro conocimiento y la necesidad de evidencia honesta. La “evidencia honesta” se vincula estrechamente con la ética y la responsabilidad epistemológica. En términos filosóficos y epistemológicos, se refiere a la información, hechos o razones que uno posee y considera de manera objetiva y sincera al formar o sostener una creencia. No se trata solo de que la evidencia exista, sino de que uno la considere y la use con integridad intelectual.
¿Podemos demostrar que el conocimiento requiere una justificación doxástica sin argumentar desde la suposición de que las creencias justificadas son creencias permisiblemente sostenidas? Supongamos que es posible conocer algo sin creerlo justificadamente y que es posible creer algo sin conocerlo. Supongamos que Rogelio cree justificadamente que P sin saber que esto es así, y que sabe que P implica Q sin creer justificadamente que esto es así. Si Rogelio deduce competentemente Q, ¿cuál es el estado de la creencia de Rogelio? No tiene conocimiento de ambas premisas, por lo que parece que Rogelio no sabe Q. Seguramente hay algo epistémicamente bueno para una creencia que se deduce de manera competente de un conjunto de premisas conocidas o justificadamente creídas. Si no es una justificación, ¿cuál sería? Dado que no parece haber una buena respuesta a esta pregunta, tal vez deberíamos decir que Rogelio creyó justificadamente cada una de las premisas de su deducción después de todo.
Lo podemos explicar así la relación entre justificación doxástica, conocimiento y deducción competente.
Planteamiento de la hipótesis
Supongamos que Rogelio cree justificadamente que P, pero no sabe que P es verdad.
Además, sabe que P→Q, pero no cree justificadamente que esta implicación sea verdadera.
Rogelio deduce competentemente Q.
Estado de la creencia de Rogelio sobre Q
Para que alguien conozca Q a partir de premisas, usualmente se requiere que tenga justificación para todas las premisas relevantes.
Rogelio no tiene justificación doxástica sobre la segunda premisa (P→Q). Por lo tanto, no cumple los criterios estándares de conocimiento: no sabe Q.
Sin embargo, la deducción competente sugiere que hay algo "epistémicamente bueno" en su creencia sobre Q, porque siguió un razonamiento correcto.
Justificación doxástica de la deducción
La dificultad que señalamos es: si no llamamos "justificación" a esta propiedad epistémica derivada de la deducción competente, ¿cómo explicamos el hecho de que su creencia en Q sea epistemológicamente valiosa?
Esto lleva a la idea de que una creencia derivada de una deducción competente debería contarse como justificada (doxásticamente), incluso si no se justificaba plenamente la implicación P→Q.
En otras palabras, la justificación doxástica puede verse como inherente al proceso de deducción competente: el razonamiento correcto "eleva" la creencia a un estado de justificación.
Conclusión parcial
Aunque inicialmente supusimos que Rogelio no tenía justificación doxástica para una de las premisas, el hecho de que deduzca correctamente Q nos fuerza a reconsiderar: su creencia en
Q es justificadamente sostenida, por la virtud epistemológica del razonamiento.
Esto sugiere que la justificación doxástica no se puede eludir si queremos preservar la idea de que el conocimiento es la creencia verdadera y justificada.
En términos simples: para que el conocimiento funcione como concepto, la justificación doxástica no es opcional, sino que es una condición necesaria.
Volviendo ahora a la pregunta Q2, es obvio que la justificación proposicional no es suficiente para el conocimiento. Puedes tener suficiente justificación proposicional para proposiciones que nunca has considerado, pero no puedes conocer P sin haber tenido P en mente. También está claro que la justificación personal no requiere conocimiento. Podemos estar personalmente justificados para creer en proposiciones verdaderas sin saber que son verdaderas.
Monedas. Supongamos que Rogelio y Luis han solicitado un determinado trabajo. Y supongamos que Rogelio tiene una fuerte evidencia para la siguiente proposición conjuntiva:
“Luis es el hombre que conseguirá el trabajo, y Rogelio tiene diez monedas en el bolsillo”.
La evidencia de Rogelio para esta proposición podría ser que el presidente de la compañía le aseguró que Luis finalmente sería seleccionado, y que él, Rogelio, había contado las monedas en el bolsillo de Luis hace diez minutos. La proposición implica:
“El hombre que conseguirá el trabajo tiene diez monedas en el bolsillo”.
Supongamos que Rogelio ve la implicación de la proposición y la acepta sobre la base de pruebas sólidas. En este caso, Rogelio está claramente justificado al creer que es verdadera. Pero imaginemos, además, que sin que Rogelio lo sepa, él mismo —y no Luis— obtiene el trabajo. Y, también sin que lo sepa, él mismo tiene diez monedas en el bolsillo. La proposición “El hombre que conseguirá el trabajo tiene diez monedas en el bolsillo” resulta verdadera, aunque la proposición “Luis es el hombre que conseguirá el trabajo, y Rogelio tiene diez monedas en el bolsillo” es falsa.
Este ejemplo clásico (tomado de Edmund Gettier) ilumina con precisión la tensión entre creencia justificada y conocimiento verdadero. Muestra que no basta con que alguien esté justificado y que, además, su creencia sea verdadera: puede haber una desconexión fatal entre las razones que sostienen la creencia y la verdad de la proposición. El caso de las “diez monedas” obliga a replantear la definición tradicional de conocimiento como “creencia verdadera justificada”. Lo interesante aquí es que el conocimiento no depende solo de la verdad y de la justificación, sino de una relación más profunda y no accidental entre ambas. Esa es la herida que Gettier abre en la epistemología contemporánea: la verdad, la creencia y la justificación pueden alinearse… pero por accidente[61].
En nuestro enfoque principal de la noción de justificación, nos centraremos en la versión doxástica. Esto no se debe a que la noción de justificación personal carezca de interés, sino a que la justificación doxástica es la noción más íntimamente conectada con cuestiones relacionadas con el deber epistémico y el derecho a creer. Me complace admitir que la justificación personal es una noción internista en el sentido de que, si persigues tus fines epistémicos de manera responsable, depende completamente de las condiciones comunes a ti y a aquellos internamente semejantes a ti; por ejemplo, cómo te parecen las cosas y cómo razonas dadas las consideraciones que tienes en mente. La pregunta interesante, en mi opinión, es si el derecho a creer lo que crees podría depender de algo externo a ti. Si no es así, tal vez el hecho de que creas con justificación no dependa de si eres afortunado y las cosas te salen bien.
Lógica simbólica y tablas de verdad
1.11 Método indirecto de decisión de la tabla de verdad
En el método de la tabla de verdad, para averiguar el valor de verdad de la proposición simbólica, necesitamos dibujar columnas y filas dependiendo del número de variables proposicionales y conectivos lógicos que tiene. Si una proposición tiene más de tres variables proposicionales y algunas conectivas lógicas, entonces el ejercicio de la tabla de verdad resulta en inconvenientes, molestias e incomodidad. Además, adaptar el procedimiento del método de la tabla de verdad para determinar la validez o invalidez de un argumento requeriría una tabla grande con muchas filas y columnas. Para evitar la incomodidad y la torpeza del ejercicio, los lógicos desarrollaron un método más corto conocido como reductio ad absurdum o método indirecto de decisión de la tabla de verdad para determinar la validez e invalidez de un argumento. En un método tabular de verdad, los valores de verdad que se encuentran bajo el conectivo lógico principal de una proposición determinan si la proposición se considera una tautología, una contradicción o una contingencia. Pero en el caso del método indirecto de decisión de tabla de verdad, comenzamos asumiendo que las premisas o proposiciones del argumento son verdaderas (T) y la conclusión es falsa (F). Más precisamente, asumimos que la forma del argumento no es válida y escribimos "F" debajo de la conectiva lógica principal del argumento.
En el método tabular de verdad, se encuentra el valor de verdad de la conectiva lógica principal del argumento al final del ejercicio, pero en el caso del método indirecto de decisión de tabla de verdad, el ejercicio tiene que comenzar con la conectiva lógica principal del argumento. Después de asignar "F" bajo la conectiva lógica principal del argumento, aplicamos las reglas básicas de las funciones de verdad de las conectivas lógicas y averiguamos los valores de verdad de todas las variables proposicionales del argumento. De ahí en adelante, necesitamos examinar si la suposición "F" ocurre en el conectivo lógico principal del argumento ha llevado a una contradicción de las reglas básicas del procedimiento de la tabla de verdad. Si no encontramos ninguna contradicción al final del ejercicio, entonces el argumento es inválido. Es así porque la hipótesis resultará correcta. Pero si la contradicción se encuentra al final del ejercicio, entonces se contradice la hipótesis asumida al principio "F". Por tanto, la hipótesis "F" se tratará como incorrecta. La suposición "F" debería haber sido "T" en su lugar. Por lo tanto, el argumento se trata como un argumento válido. El método indirecto de decisión de la tabla de verdad se explica con la ayuda de los siguientes ejemplos.
Ejemplo-1: (((p → q) ∧ p) → q)
Este argumento consta de dos premisas "(p → q)" y "p" y una conclusión "q". La conclusión q ’se deriva de dos premisas. Hay dos variables proposicionales p y q , y dos conectivos lógicos " → "y" ∧ " están asociados con este argumento. La conexión lógica principal del argumento es "→". Este argumento establece que si "(p → q)" y "p" entonces podemos sacar una conclusión "q". Ahora, averiguaremos si el argumento es
Paso 1:
 13.40.40.png)
Comenzamos asumiendo que la forma del argumento no es válida. Por lo tanto, asignamos "F" bajo la conectiva lógica principal del argumento.
Paso 2:
 13.40.45.png)
La columna conectiva lógica principal puede ser falsa solo cuando el antecedente "(p → q) ∧ p)" es verdadero y el consecuente "q" es falso. Entonces, tenemos el valor de verdad de "q", es decir, "F".
Paso 3:
 13.40.50.png)
Acerca del antecedente del argumento, el conectivo lógico principal "∧" es verdadero cuando "(p → q)" es T y "p" es T. Aquí, hemos obtenido el valor de verdad de "p".
Paso 4:
 13.40.55.png)
Obtuvimos el valor de verdad de "p" como T y "q" como F. Los valores de verdad de estas variables proposicionales se asignan en "(p → q)". Después de asignar los valores de verdad a "(p → q)", encontramos que hay inconsistencia en la expresión "(p → q)". Es decir, cuando p es T y q es F, la función de verdad de (p → q) es T. El valor de verdad (p → q) debería haber sido F. una contradicción en el resultado basado en nuestra suposición. La suposición debe tener T en el lugar de F. Dado que la suposición bajo la conectiva lógica principal es T, todo el argumento se trata como un argumento válido.
Ejemplo-2: {(p → q) → ~ (p ∧ (q ∧ r))}
Este argumento consta de una premisa “(p → q)” y una conclusión “~ (p ∧ (q ∧ r))” . La conclusión "~ (p ∧ (q ∧ r))" se deriva de la premisa. El argumento tiene tres variables proposicionales; "P", "q" y "r", dos conectivos lógicos; ‘→’ y ‘∧’, y una constante lógica ‘~’. La conexión lógica principal del argumento es "→". Este argumento establece que si ‘(p → q)’ entonces ‘~ (p ∧ (q ∧ r))’, como conclusión. Ahora, descubriremos la validez del argumento adoptando el método indirecto de decisión de la tabla de verdad.
Paso 1:
 13.47.37.png)
Comenzamos asumiendo que la forma del argumento no es válida. Por lo tanto, asignamos "F" bajo la conectiva lógica principal del argumento.
Paso 2:
 13.47.41.png)
La columna conectiva lógica principal puede ser falsa cuando el antecedente "(p → q)" es verdadero y el consecuente "~ (p ∧ (q ∧ r))" es falso.
Paso 3:
 13.47.46.png)
Acerca del consecuente del argumento, si el valor de verdad de ‘~ (p ∧ (q ∧ r))’ es F, entonces el valor de verdad de ‘(p ∧ (q ∧ r))’ es T.
Paso 4:
 13.47.51.png)
El valor de verdad de “(p’ (q ‘r))” es T cuando “p” es T y “(q’ r)”’ es T. Aquí, obtuvimos el valor de verdad de “p” como T.
Paso 5:
 13.47.56.png)
El valor de verdad de “(q ∧ r)” es T si y solo si “q” es T y “r” es T. En este paso, obtuvimos el valor de verdad de “q” como T y “r” como F.
Paso 6:
 13.48.01.png)
Obtuvimos el valor de verdad de "p" como T y "q" como T. El valor de verdad de estas variables proposicionales se asigna a "(p → q)". Después de asignar los valores de verdad en "(p → q)", encontramos que no hay inconsistencia en la expresión "(p → q)". Es decir, cuando "p" es T y "q" es T, la función de verdad de "(p → q)" es T. Por lo tanto, no encontramos ninguna contradicción en el resultado basado en nuestra suposición. La suposición F era correcta. Dado que la suposición bajo la conectiva lógica principal era F y es correcta, todo el argumento se trata como un argumento inválido.
Ejemplo-3: [{((p → q) ∧ (s → r)) ∧ (q → s)} → (p ∨ r)]
Este argumento consta de tres premisas “(p → q)”, “(s → r)”, “(q → s)” y una conclusión “(p ∨ r)”. La conclusión "(p ∨ r)" se deriva de tres premisas. Este argumento tiene cuatro variables proposicionales "p", "q", "r" y "s" y tres conectivos lógicos "→", "∧" y "∨". La conexión lógica principal del argumento es "→". Este argumento establece que si "(p → q)", "(s → r)" y "(q → s)", entonces "(p ∨ r)" es la conclusión. Ahora, descubriremos la validez del argumento adoptando el método indirecto de decisión de la tabla de verdad.
Paso 1:
 13.53.08.png)
Comenzamos asumiendo que la forma del argumento no es válida. Por lo tanto, asignamos "F" bajo la conectiva lógica principal del argumento.
Paso 2:
 13.53.12.png)
La columna conectiva lógica principal puede ser falsa cuando el antecedente “{((p → q) ∧ (s → r)) ∧ (q → s)}” es verdadero y el consecuente “(p ∨ r)” es falso.
Paso 3:
 13.53.17.png)
Con respecto al consecuente “(p ∨ r)” del argumento, el valor de verdad de “(p ∨ r)” es F cuando “p” es F y “r” es F. En este paso, obtuvimos la verdad- valores de “p” y “r” como F.
Paso 4:
 13.53.21.png)
La conectiva lógica principal del antecedente “{((p → q) ∧ (s → r)) ∧ (q → s)}” es “∧”. El antecedente consta de dos partes “((p → q) ∧ (s → r))” y “(q → s)”. Ya obtuvimos que el valor de verdad bajo la conectiva lógica principal del antecedente es T. El valor de verdad del antecedente es T cuando los valores de verdad de sus dos partes constituyentes son T.
Paso 5:
 13.53.26.png)
El valor de verdad de la proposición compuesta "((p → q) ∧ (s → r))" es T cuando "(p → q)" es T y "(s → r)" es T.
Paso 6:
 13.53.31.png)
Ya hemos obtenido el valor de verdad de "p" y "r", que ponemos en las proposiciones "(p → q)" y "(s → r)".
Paso 7:
 13.53.36.png)
Con respecto a la proposición “(s → r)”, cuando “s” es F y “r” es F, el valor de verdad de la proposición “(s → r)” es T. En este paso, obtuvimos el valor de verdad de “s” como F. Hemos mencionado que el valor de verdad de “s” es F en la proposición “(q → s)”.
Paso 8:
 13.53.41.png)
Tras la consideración de la proposición compuesta “(q → s)”, podemos asignar que el valor de verdad de “q” es F. Es así porque el valor de verdad de “(q → s)” es T cuando q es F y s es F. En este paso, obtuvimos el valor de verdad de q como F. El valor de verdad de q se menciona en la proposición (p → q). Después de asignar el valor de verdad en "(p → q)", "(s → r)" y "(q → s)", encontramos que no hay inconsistencia en estas premisas. Por lo tanto, no encontramos ninguna contradicción en el resultado basado en nuestro supuesto. Se demostró que la suposición F era correcta. Dado que la suposición bajo la conectiva lógica principal era F y es correcta, todo el argumento se trata como un argumento inválido. Además del método indirecto de decisión de la tabla de verdad, existe otro método conocido como "cuadros analíticos" o "árboles" que existe para determinar la validez e invalidez de un argumento. El método de los "árboles" se conoce popularmente como "árboles de Beth", ya que el profesor Evert Willem Beth (1908-1964) lo introdujo en la lógica y el discurso lógico. El profesor Beth es conocido por su contribución al desarrollo del "método de cuadros semánticos (1955)" conocido como "árbol de Beth" y "árbol de la verdad".
1.12 Árbol de Beth
El árbol de Beth es un método que ayuda a determinar la validez de un argumento. Para examinar un argumento, necesitamos organizar sus premisas y conclusión en una lista. Necesitamos negar la conclusión mientras la mencionamos en la lista. La razón es que necesitamos verificar si el argumento se satisface o no con una conclusión negativa. Tras nuestro examen, si encontramos que las premisas no son verdaderas juntas, entonces el argumento es válido. La razón es que al menos una de sus premisas contradice la conclusión negativa, que se tomó como un supuesto al enumerar la conclusión antes de iniciar la verificación. Si todas las premisas son verdaderas, entonces el argumento no es válido porque la conclusión negativa es correcta. Para probar un argumento a través del método del árbol de verdad, debemos cumplir con las siguientes reglas y procedimientos. Reglas del árbol de la verdad Las reglas del árbol de Beth se emplean para desarrollar las ramas o cerrarlas. Para eso, necesitamos ramificar una proposición o apilar la ramificación de la siguiente manera.
Procedimientos del árbol de la verdad:
(i) La construcción del árbol de la verdad comienza con el conectivo lógico principal de una proposición simbólica.
(ii) La construcción del árbol de la verdad avanza hacia abajo, mientras que la evaluación de las ramas avanza hacia arriba.
(iii) Las proposiciones que implican apilamiento deben descomponerse antes que las proposiciones que implican ramificaciones.
(iv) Siempre que se descompone una proposición, se coloca una marca de verificación a su derecha. Las proposiciones marcadas se ignoran en el momento de la evaluación de la rama.
(v) Se dice que una construcción de árbol de verdad está terminada cuando la proposición dada se descompone completamente en una proposición simple o una proposición simple negada.
(vi) Una rama se cierra si y solo si contiene una contradicción. Esa rama se bloquea colocando una "x" en el extremo inferior.
(vii) Cualquier sucursal que no esté cerrada se dice que está abierta. Dichas sucursales se notifican colocando un "0" en el extremo inferior.
(viii) Un árbol de verdad se cierra si y solo si sus ramas están cerradas.
(ix) Cuando todas las ramas de un árbol de verdad están cerradas debido a la auto-contradicción, el argumento se trata como válido; de lo contrario, el argumento se considera inválido.
Con estos procedimientos y reglas del árbol de verdad, averigüemos la validez de los siguientes argumentos que se presentan a través de proposiciones simbólicas.
(a) (((p → q) ∧ ~ q) → ~ p)
(b) (((p → q) ∧ p) → q)
(c) {(p → (p → q)) → ((p → q) → (q → p))}
(d) {((p → q) ∧ (~ r → ~ q)) → (p → r)}
Ejemplo-1: (((p → q) ∧ ~ q) → ~ p)
Este argumento tiene dos premisas "(p → q)" y "~q" y una conclusión "~p". Enumeremos las premisas y la conclusión según los procedimientos del árbol de verdad.
Paso 1:
 14.03.34.png)
En el paso 1, después de enumerar las premisas, negamos la conclusión "~ p", que se convierte en "~~ p".
Paso 2:
 14.03.40.png)
En el paso 2, colocamos la marca de verificación a la derecha de "~ q" y "p" ya que ambas proposiciones se descomponen. La proposición "~~ p" se apila en "p".
Paso 3:
 14.03.44.png)
En el paso 3, descomponemos la proposición "(p → q)" y colocamos la marca de verificación a la derecha de ella. Encontramos las ramas "~ p" y "q", y no queda más proposición que descomponer. Tras la evaluación de la rama de este árbol de verdad a través del movimiento ascendente, encontramos "p" y "~ p", "q" y "~ q". Por tanto, el árbol de la verdad contiene auto-contradicción. Como resultado, bloqueamos la rama "~ p" y "q" colocando "x" en la parte inferior. Dado que todas las ramas de este árbol de verdad están cerradas y se involucran en autocontradicciones, el argumento no se satisface. Significa, la negación a la conclusión, que colocó al enumerar el argumento, no es correcta. Por tanto, las premisas dadas (proposiciones) y la conclusión juntas se tratan como un argumento válido.
Ejemplo-2: (((p → q) ∧ p) → q)
Este argumento tiene dos premisas "(p → q)" y "p" y una conclusión "q". Enumeremos las premisas y la conclusión según los procedimientos del árbol de verdad.
Paso 1:
 14.06.16.png)
En el paso 1, después de enumerar las premisas, negamos la conclusión "q" que se convierte en "~ q".
Paso 2:
 14.06.21.png)
En el paso 2, colocamos la marca de verificación a la derecha de la "p" y "~ q", ya que ambas proposiciones están descompuestas.
Paso 3:
 14.06.25.png)
En el paso 3, descomponemos la proposición "(p → q)" y le ponemos la marca de verificación. Encontramos las ramas “~ p” y “q”, y no queda más proposición que descomponer aún más. Tras la evaluación de la rama de este árbol de verdad a través del movimiento ascendente, encontramos en la rama izquierda "p" y "~ p", en la rama derecha "q" y "~ q".
Por tanto, el árbol de la verdad contiene auto-contradicción. Como resultado, bloqueamos la rama "~ p" y "q" colocando "x" en la parte inferior. Dado que todas las ramas de este árbol de verdad están cerradas y se involucran en autocontradicciones, el argumento no se satisface. Significa, la negación a la conclusión, que colocó al enumerar el argumento, no es correcta. Por tanto, las premisas dadas (proposiciones) y su conclusión juntas se consideran un argumento válido.
Ejemplo-3: {(p → (p → q)) → ((p → q) → (q → p))}
Enumeremos la premisa y la conclusión según los procedimientos del árbol de verdad. Paso 1:
 14.08.23.png)
En el paso 1, después de enumerar la premisa, negamos la conclusión, es decir, "~ ((p → q) → (q → p))".
Paso 2:
 14.08.27.png)
En el paso 2, aplicamos la regla del árbol de verdad "~ (a → b)" y apilamos las proposiciones. También colocamos una marca de verificación a la derecha de la proposición para su descomposición.
Paso 3:
 14.08.31.png)
En el paso 3, aplicamos la regla del árbol de verdad "~ (a → b)" y apilamos las proposiciones también, colocamos una marca de verificación a la derecha de la proposición compuesta para su descomposición.
Paso 4:
 14.08.37.png)
En el paso 4, aplicamos la regla del árbol de verdad "(a → b)" y ramificamos las proposiciones. También colocamos una marca de verificación a la derecha de la proposición compuesta para su descomposición.
Paso 5:
 14.08.42.png)
En el paso 5, aplicamos la regla del árbol de verdad "(a → b)" y ramificamos las proposiciones. También colocamos una marca de verificación a la derecha de la proposición compuesta para su descomposición. Pero la descomposición de la proposición compuesta aún no está completa. Tras la evaluación de la rama izquierda “~ p”, encontramos que esta proposición no implica autocontradicción; por lo tanto, colocamos "0" en su extremo inferior. Es una propuesta autoconsistente. Nuevamente, al considerar la rama derecha "~ p" del árbol, se encuentra que no está resultando en una auto-contradicción. Por lo tanto, la rama está marcada con "0" en su extremo inferior.
Paso 6:
 14.08.48.png)
En el paso 6, aplicamos la regla del árbol de verdad "(a → b)" y ramificamos las proposiciones. También colocamos una marca de verificación a la derecha de la proposición compuesta para su descomposición. En este paso, todas las proposiciones se descomponen en una proposición simple o una proposición negada. Tras la evaluación de la rama extrema izquierda "~p" y "q", encontramos que estas proposiciones no implican una auto-contradicción. Son proposiciones autoconsistentes. De manera similar, tras la evaluación de "~p" y "q" de la rama derecha del árbol de verdad, encontramos que estas proposiciones tampoco implican autocontradicción. Son proposiciones autoconsistentes. Dado que todas las ramas de este árbol de verdad no están cerradas y no implican una auto-contradicción, el argumento está satisfecho. Significa, la negación de la conclusión, que se coloca al enumerar el argumento, es correcta. Por tanto, las premisas dadas (proposiciones) y su conclusión juntas se consideran un argumento inválido.
Ejemplo-4: {((p → q) ∧ (~ r → ~ q)) → (p → r)}
Enumeremos la premisa y la conclusión según los procedimientos del árbol de verdad.
Paso 1:
 14.14.52.png)
En el paso 1, después de enumerar las premisas, negamos la conclusión, es decir, "~(p→ r)".
Paso 2:
 14.14.56.png)
En el paso 2, aplicamos la regla del árbol de verdad "~ (a → b)" y apilamos las proposiciones. También colocamos una marca de verificación a la derecha de la proposición compuesta para su descomposición.
Paso 3:
 14.15.01.png)
En el paso 3, aplicamos la regla del árbol de verdad “(a → b)” y ramificamos las proposiciones. También colocamos una marca de verificación a la derecha de la proposición compuesta para su descomposición. Además aplicamos la regla del árbol de verdad “~~ a” a descomponer la rama del lado izquierdo, es decir “~~ r”. Colocamos una marca de verificación a la derecha de la proposición doble negativa para su descomposición.
Paso 4:
 14.15.08.png)
En el paso 4, aplicamos la regla del árbol de verdad "(a → b)" y ramificamos las proposiciones. También colocamos una marca de verificación a la derecha de la proposición compuesta para su descomposición. Tras la evaluación de la rama extrema izquierda "r" y dos ramas de la derecha "~ p" y "q", encontramos que estas proposiciones implican una auto-contradicción. Por lo tanto, ponemos "x" en la parte inferior. Dado que todas las ramas de este árbol de verdad están cerradas y se involucran en una auto-contradicción, el argumento no se satisface. Significa negación a la conclusión, que colocada al enumerar el argumento, es incorrecta. Por tanto, las premisas dadas (proposiciones) y su conclusión juntas se consideran un argumento válido.
1.13 Fórmulas de derivación proposicional
Las fórmulas de derivación proposicional se conocen como "reglas de reemplazo". Afirma que una proposición puede derivarse de otra proposición que tenga un valor de verdad similar. En otras palabras, una proposición puede reemplazar a otra proposición, ya que son equivalentes entre sí y tienen un valor de verdad similar.
Fórmula-1: ∼∼a ≡ a
Esta fórmula establece que la negación de la negación de una proposición es la proposición misma. Entonces, la doble negación se convierte en afirmación.
Fórmula-2: (a ∧ b) ≡ (b ∧ a)
Esta fórmula se conoce como ley conmutativa. Enuncia que a y b es igual ab y a.
Fórmula-3: (a ∨ b) ≡ (b ∨ a)
Esta fórmula se conoce también como ley conmutativa. Enuncia que a o b es igual a b o a.
Fórmula-4: (a ∧ (b ∧ c)) ≡ ((a ∧ b) ∧ c)
Esta fórmula se conoce como ley asociativa. Expresa que a, b y c es igual a “a y b”, y c. Fórmula-5: (a ∨ (b ∨ c)) ≡ ((a ∨ b) ∨ c)
Esta fórmula también se conoce como ley asociativa. Expresa que a, b o c es igual a a o b, o c.
Fórmula-6: (a ∧ (b ∨ c)) ≡ ((a ∧ b) ∨ (a ∧ c)) Esta fórmula se llama ley distributiva. Se lee como a, y b o c es igual a a y b o a y c.
Fórmula-7: (a ∨ (b ∧ c)) ≡ ((a ∨ b) ∧ (a ∨ c))
Esta fórmula se llama ley distributiva. Se lee como a o, b y c es igual a a o b y a o c.
Fórmula 8: (a ∧ b) ≡∼ (∼ a∨ ∼ b)
Esta fórmula se denomina ley de DeMorgan. Se lee como “a y b” es igual a la negación de la "negación de a" o "negación de b". El valor de verdad de "(a ∧ b)" y el valor de verdad de "~ (~ a ∨ ~ b)" son idénticos entre sí. En este caso, una proposición compuesta disyuntiva se deriva de una proposición conjuntiva. Para explicar, una proposición en la que ocurre la conjunción puede expresarse a través de la disyunción si negamos tanto los componentes de la conjunción como la conjunción misma.
Fórmula 9: (a ∨ b) ≡∼ (∼ a∧ ∼ b)
Esta fórmula también se denomina ley de De Morgan. Se lee como a o b es igual a la negación de la "negación de a" y la "negación de b". El valor de verdad de "(a ∨ b)" y el valor de verdad de "~ (~ a ∧ ~ b)" son idénticos entre sí. En este caso, una proposición compuesta conjuntiva se deriva de una proposición disyuntiva. Para explicar, una proposición en la que ocurre una disyunción puede expresarse a través de la conjunción si negamos tanto los componentes de la disyunción como la disyunción misma.
Fórmula-10: (a → b) ≡ (∼ b → ∼ a)
Esta fórmula se conoce como ley de contraposición. Se lee como a implica que b es igual a la negación de b implica la "negación de a". El valor de verdad de "(a → b)" es idéntico al valor de verdad de "(~ b → ~ a)". Expresa que una proposición compuesta de implicación puede reducirse a una proposición compuesta de implicación siempre que necesitemos intercambiar su antecedente y su consecuente negando ambos.
Fórmula 11: (a → b) ≡ (∼ a ∨ b)
Esta fórmula es una definición de implicación material. Se lee como a implica que b es igual a la negación de a o b. El valor de verdad de "(a → b)" es idéntico al valor de verdad de "(~ a ∨ b)". Establece que una proposición compuesta de implicación se puede expresar en la forma de proposición disyuntiva siempre que el antecedente de la proposición implicativa se niegue en la proposición compuesta disyuntiva.
Fórmula-12: (a → b) ≡∼ (a∧ ∼ b)
Esta fórmula también es una definición de implicación material. Se lee como a implica que b es igual a la negación de a y la negación de b. El valor de verdad de "(a → b)" es idéntico al valor de verdad de "~ (a ∧ ~ b)". Esta fórmula enuncia que una proposición compuesta de implicación puede expresarse en forma de proposición conjuntiva siempre que el consecuente de la proposición implicativa se niegue en la proposición conjuntiva y la proposición conjuntiva se niegue a sí misma.
Fórmula-13: {((a → b) ∧ (b → c)) → (a → c)} Esta fórmula se conoce como transitividad de implicación. Se lee como si a implica b y b implica c, entonces a implica c. Establece que si una proposición "a" implica otra proposición "b" y la proposición "b" implica "c", entonces la proposición "a" implica "c" necesariamente.
Fórmula 14:
(i) ((a → b) ∧ a) → b
(ii) ((a → b) ∧ ∼ b) → ∼ a
Estas fórmulas se conocen como la ley del desprendimiento. Transmite que si el antecedente de una proposición implicativa se afirma junto con la proposición implicativa, se sigue el consecuente de la proposición implicativa. Además, establece que si el consecuente de una proposición implicativa se niega junto con la proposición implicativa, entonces sigue la negación del antecedente de la proposición implicativa.
Fórmula-15: (a ≡ b) ≡ ((a → b) ∧ (b → a))
Esta fórmula se llama equivalencia material. Se lee como una equivalencia b es igual a a implica b y b implica a. El valor de verdad de "(a ≡ b)" es idéntico al valor de verdad de "((a → b) ∧ (b → a))". Expresa que una proposición compuesta de equivalencia se puede reducir a una combinación de forma de proposición lógica de implicación y conjunción.
Fórmula 16: (a ≡ b) ≡ ((a ∧ b) ∨ (∼ a∧ ∼ b))
Esta fórmula también se denomina equivalencia de material. Se lee, una equivalencia b es igual a “a y b” o negación de ay negación de b. El valor de verdad de "(a ≡ b)" es idéntico al valor de verdad de "((a ∧ b) ∨ (~ a ∧ ~ b))". Expresa que una proposición compuesta de equivalencia puede reducirse a una combinación de forma de proposición lógica de conjunción y disyunción.
Fórmula 17: ((a ∧ b) → c) ≡ (a → (b → c)) Esta fórmula también se denomina ley de exportación. Se lee si “a y b” entonces c es equivalente a a implica, b implica c. El valor de verdad de "((a ∧ b) → c)" es idéntico al valor de verdad de "(a → (b → c))". Transmite que una combinación de proposición de implicación y conjunción puede reducirse a una forma de proposición de implicación.
Fórmula-18: (a ∨ a) ≡ a Esta fórmula se llama ley de tautología. Se lee que a o a es equivalente a a.
Fórmula-19: (a ∧ a) ≡ a Esta fórmula también se llama ley de tautología. Se lee que a y a es equivalente a a.
Fórmula 20:
(i) (a ∧ b) → a
(ii) (a ∧ b) → b
Hemos mencionado dos fórmulas en la fórmula 20 debido a su naturaleza similar. El primero se lee como a y b implica a, mientras que el segundo se lee como a y b implica b. Esta fórmula enuncia que la conjunción implica cualquiera de las proposiciones unidas.
Fórmula-21: (p∨ ∼ p)
Esta fórmula se conoce como la ley del medio excluido. Se lee p o negación p. Afirma que toda proposición debe ser verdadera o falsa. Si se niega una opción entre dos alternativas, se aceptará la otra. Las fórmulas anteriores se mencionan en la tabla a continuación para referencia y uso inmediato.
 13.20.33.png)
Usaremos estas fórmulas para reducir las proposiciones simbólicas a la forma normal conjuntiva (CNF) o la forma normal disyuntiva (DNF). El objetivo de reducir una proposición simbólica dada a DNF o CNF es descubrir el valor de verdad de la proposición, ya sea una tautología o no. El DNF y el CNF se consideran "métodos de procedimiento de decisión" para determinar el valor de verdad de las proposiciones simbólicas compuestas y complejas.
1.14 Forma normal disyuntiva
La forma normal disyuntiva (DNF) es aquella en la que una proposición simbólica se puede transformar en una expresión que consiste en una disyunción de conjunciones. En este caso, la conjunción consta de variables proposicionales y sus negaciones, y cada proposición conjuntiva está conectada con otra proposición conjuntiva a través de una conectiva lógica disyuntiva. La disyunción construida a partir de estas conjunciones retrata un ordenación y horquillado estándar. Por ejemplo,
. . . (∼ a ∧ b) ∨ (segundo ∧ p) ∨ (∼ p ∧ a) ∨ ∼ p. . .
Al aplicar las fórmulas anteriores, podemos transformar una proposición simbólica en la forma DNF. Al convertir la proposición simbólica en la forma DNF, debemos hacer lo siguiente. Primero, elimine todas las negaciones dobles aplicando la fórmula 1. En segundo lugar, aplique las fórmulas de implicación material (fórmulas 11 y 12) y convierta la proposición en su forma equivalente. En tercer lugar, aplique las leyes de De Morgan (fórmulas 8 y 9) para deshacerse de los corchetes. Necesitamos continuar aplicando otras fórmulas cuando sea necesario mientras convertimos la proposición simbólica en DNF. En el DNF, debemos encontrar una proposición o su negación que se conecte con "∨". Si no se encuentra una variable proposicional atómica, entonces debe haber proposiciones conjuntivas compuestas que consistan en variables proposicionales atómicas o su negación conectada con el conectivo lógico '∧', y cada proposición conjuntiva está conectada con otra proposición conjuntiva con una disyunción '∨' . Además, no habrá una proposición conjuntiva compuesta negativa en la forma DNF. Un DNF se considera tautología cuando uno de sus elementos es verdadero. Significa que el valor de verdad de uno de los conjuntos debe ser verdadero. Una vez más, una proposición compuesta conjuntiva es verdadera cuando los valores de verdad de sus variables proposicionales son verdaderos. Ahora, convierta las siguientes proposiciones simbólicas en DNF aplicando las fórmulas anteriores y averigüemos si estas proposiciones son tautología o no.
(i) {((p → q) ∧ ~ q) → ~ p}
(ii) {((p → q) ∧ p) → q}
(iii) ~ (p → q) → (~ r ∨ p)
Ejemplo-1: {((p → q) ∧ ~ q) → ~ p}
{((p → q) ∧ ~ q) → ~ p} Esta proposición se nos da
= ~ ((p → q) ∧ ~ q) ∨ ~ p Fórmula aplicada-11
= ~ ((~ p ∨ q) ∧ ~ q) ∨ ~ p Fórmula aplicada-11
= (~ (~ p ∨ q) ∨ ~~ q) ∨ ~ p Fórmula aplicada-9
= (~ (~ p ∨ q) ∨ q) ∨ ~ p Fórmula aplicada-1
= ((p ∧ ~ q) ∨ q) ∨ ~ p Fórmula aplicada-8
= ((p ∨ q) ∧ (~ q ∨ q)) ∨ ~ p Fórmula aplicada-7
= ((q ∨ p) ∧ (q ∨ ~ q)) ∨ ~ p Fórmula aplicada-3
= (q ∨ (p ∧ ~ q)) ∨ ~ p Fórmula aplicada-7
= (p ∧ ~ q) ∨ ~ p ∨ q Fórmula aplicada-3 (Esto es DNF)
Esta expresión está ahora en forma disyuntiva normal. Es así porque, dentro del corchete, encontramos que “p” y “~ q” están conectados con el operador lógico conjuntivo. La proposición entre corchetes y otras variables proposicionales están conectadas con un operador lógico disyuntivo. Encontramos "p" y "~ p", "q" y "~ q" en el DNF; estos están conectados con la disyunción, y el valor de verdad de "p" “~ p" y "q" “~ q" es verdadero cuando al menos una de las variables proposicionales es verdadera. Por tanto, toda la expresión es una tautología.
Ejemplo-2: {((p → q) ∧ p) → q}
{((p → q) ∧ p) → q} Esta proposición se nos da
= ~ ((p → q) ∧ p) ∨ q Fórmula aplicada-11
= ~ ((~ p ∨ q) ∧ p) ∨ q Fórmula aplicada-11
= (~ (~ p ∨ q) ∨ ~ p) ∨ q Fórmula aplicada-8
= (~~ (p ∧ ~ q) ∨ ~ p) ∨ q Fórmula aplicada-9
= ((p ∧ ~ q) ∨ ~ p) ∨ q Fórmula aplicada-1
= (p ∧ ~ q) ∨ ~ p ∨ q Fórmula aplicada-15 (Esto es DNF)
Esta expresión está ahora en forma disyuntiva normal. Es así porque, dentro del corchete, encontramos que “p” y “~ q” están conectados con el operador lógico conjuntivo. La proposición entre corchetes y otras variables proposicionales están conectadas con un operador lógico disyuntivo. Encontramos "p" y "~ p", "q" y "~ q" en el DNF; éstos están conectados con la disyunción, y el valor de verdad de "p" “~ p" y "q" “~ q" es verdadero cuando al menos una de las variables proposicionales es verdadera. Por tanto, toda la expresión es una tautología.
Ejemplo-3: ~ (p → q) → (~ r ∨ p)
~ (p → q) → (~ r ∨ p) Esta proposición se nos da
= ~~ (p → q) ∨ (~ r ∨ p) Fórmula aplicada-11
= (p → q) ∨ (~ r ∨ p) Fórmula aplicada-1
= (~ p ∨ q) ∨ (~ r ∨ p) Fórmula aplicada-11
= (~ p ∨ q ∨ ~ r ∨ p) Fórmula aplicada-5 (Esto es DNF)
Esta expresión está ahora en forma disyuntiva normal. Es así porque encontramos variables proposicionales y su negación está conectada con el operador lógico disyuntivo. Encontramos "p" y "~ p" en el DNF, que están conectados con la disyunción. El valor de verdad de “p” “~ p“ es verdadero cuando al menos una de las variables proposicionales es verdadera. Por tanto, toda la expresión es una tautología.
1.15 Forma normal conjuntiva
La forma normal conjuntiva (CNF) es aquella en la que una proposición simbólica se puede convertir en una expresión que consiste en una conjunción de disyunciones. En este caso, las proposiciones disyuntivas consisten en variables proposicionales y sus negaciones, y cada proposición disyuntiva está conectada con otra proposición disyuntiva a través de un operador lógico conjuntivo. La conjunción construida a partir de las disyunciones retrata un ordenamiento y un horquillado estándar. Por ejemplo,
. . . (a∨ ∼ b) ∧ (∼ c∨ ∼ b) ∧ (∼ c ∨ a) ∧ ∼ a. . .
Al aplicar las fórmulas de derivación proposicional, podemos convertir una proposición simbólica en la forma CNF. Al convertir la proposición simbólica en forma CNF, debemos hacer lo siguiente. Primero, elimine todas las negaciones dobles aplicando la fórmula-1. En segundo lugar, aplique fórmulas de implicación material (fórmulas 11 y 12) y convierta la proposición en su forma equivalente. En tercer lugar, aplique las leyes de De Morgan (fórmulas 8 y 9) para deshacerse de los corchetes. Necesitamos seguir adelante aplicando otras fórmulas cuando sea necesario mientras se convierte la proposición simbólica en CNF. En el CNF, si encontramos una proposición que se conecta con la misma proposición con ‘∧’, el CNF se trata como una tautología. Si no se encuentra una variable proposicional atómica en el CNF, entonces debe haber proposiciones disyuntivas compuestas que consistan en variables proposicionales atómicas o su negación conectada con el conectivo lógico '∨', y cada proposición disyuntiva está conectada con otra proposición disyuntiva con una conjunción. '∧'. Además, no habrá una proposición conjuntiva compuesta negativa en el CNF. Un CNF se considera tautología cuando el valor de verdad de ambas proposiciones disyuntivas es verdadero. Una proposición compuesta disyuntiva es verdadera cuando el valor de verdad de una de sus variables proposicionales es verdadero. Ahora, convierta las siguientes proposiciones simbólicas en CNF aplicando las fórmulas de derivación proposicional y averigüemos si estas proposiciones son tautología o no.
(i) {((p → q) ∧ p) → q}
(ii) (p → (q ∧ r)) ∧ (~ p → (~ q ∧ ~ r))
(iii) (q ∨ (p ∧ r)) ∧ ~ ((p ∨ r) ∧ q)
(iv) ((p → q) ≡ (~ p ∨ q))
Ejemplo-1: {((p → q) ∧ p) → q}
{((p → q) ∧ p) → q} Esta proposición se nos da
= ~ ((p → q) ∧ p) ∨ q Fórmula aplicada-11
= ~ ((~ p ∨ q) ∧ p) ∨ q Fórmula aplicada-11
= (~ (~ p ∨ q) ∨ ~ p) ∨ q Fórmula aplicada-9
= ((p ∧ ~ q) ∨ ~ p) ∨ q Fórmula aplicada-8
= (~ p ∨ (p ∧ ~ q)) ∨ q Fórmula aplicada-3
= ((~ p ∨ p) ∧ (~ p ∨ ~ q)) ∨ q Fórmula aplicada-7
= (~ p ∨ p ∨ q) ∧ (~ p ∨ ~ q ∨ q) Fórmula aplicada-7 (Esto es CNF)
Esta expresión está ahora en forma conjuntiva normal. Es así porque encontramos variables proposicionales y su negación están conectadas con un operador lógico disyuntivo dentro del corchete y las proposiciones disyuntivas están conectadas con un operador lógico conjuntivo. En el CNF, encontramos "p" y "~ p" en la proposición disyuntiva del lado izquierdo y "q" y "~ q" en la proposición disyuntiva del lado derecho. Dado que “p” y “~ p”, “q” y “~ q” están conectados con la disyunción, el valor de verdad de la proposición disyuntiva del lado izquierdo y la proposición disyuntiva del lado derecho sería verdadero incluso si una de sus variables proposicionales es verdadero. Además, no importa cuál sería el valor de "q" con respecto a la proposición disyuntiva del lado izquierdo y "~ p" con respecto a la proposición disyuntiva del lado derecho. La razón es que “q” y “~ p” están conectados con sus variables proposicionales con disyunción. Dado que “p” “~ p” es verdadero en la proposición disyuntiva del lado izquierdo y “q” “~ q” es verdadero en la proposición disyuntiva del lado derecho, el valor de verdad de toda la proposición disyuntiva sería verdadero. Dado que ambas proposiciones disyuntivas están unidas con conjunción y sus valores de verdad son verdaderos, el valor de verdad de toda la expresión es verdadero. Es así porque el valor de verdad de una proposición conjuntiva es verdadero cuando sus dos variables proposicionales son verdaderas. Por tanto, la expresión simbólica es una tautología.
Ejemplo-2: (p → (q ∧ r)) ∧ (~ p → (~ q ∧ ~ r))
(p → (q ∧ r)) ∧ (~ p → (~ q ∧ ~ r)) Esta proposición se nos da
= (~ p ∨ (q ∧ r)) ∧ (~~ p ∨ (~ q ∧ ~ r)) Fórmula aplicada-11
= (~ p ∨ (q ∧ r)) ∧ (p ∨ (~ q ∧ ~ r)) Fórmula aplicada-1
= (~ p ∨ q) ∧ (~ p ∨ r) ∧ (p ∨ ~ q) ∧ (p ∨ ~ r) Fórmula aplicada-7 (Esto es CNF)
Esta expresión está ahora en forma conjuntiva normal. Es así porque encontramos variables proposicionales y su negación están conectadas con un operador lógico disyuntivo dentro del corchete, y las proposiciones disyuntivas están conectadas con un operador lógico conjuntivo. En el CNF, no encontramos ni "p" ni "~ p"; "Q" y "~ q"; ni "r" y "~ r" unidos con un operador lógico disyuntivo. Por tanto, el valor de verdad de las proposiciones disyuntivas no es verdadero. Esto, a su vez, el valor de verdad de la proposición conjuntiva es falso. Por tanto, toda la proposición no es una tautología.
Ejemplo-3: (q ∨ (p ∧ r)) ∧ ~ ((p ∨ r) ∧ q)
(q ∨ (p ∧ r)) ∧ ~ ((p ∨ r) ∧ q) Esta proposición se nos da
= ((q ∨ p) ∧ (q ∨ r)) ∧ ~ ((p ∨ r) ∧ q) Fórmula aplicada-7
= ((q ∨ p) ∧ (q ∨ r)) ∧ (~ (p ∨ r) ∨ ~ q) Fórmula aplicada-8
= ((q ∨ p) ∧ (q ∨ r)) ∧ ((~ p ∧ ~ r) ∨ ~ q) Fórmula aplicada-9
= ((q ∨ p) ∧ (q ∨ r)) ∧ (~ q ∨ (~ p ∧ ~ r)) Fórmula aplicada-3
= (q ∨ p) ∧ (q ∨ r) ∧ (~ q ∨ ~ p) ∧ (~ q ∨ ~ r) Fórmula aplicada-3 (Esto es CNF)
Esta expresión está ahora en forma conjuntiva normal. Es así porque encontramos variables proposicionales y su negación están conectadas con un operador lógico disyuntivo dentro del corchete, y las proposiciones disyuntivas están conectadas con un operador lógico conjuntivo. En el CNF, no encontramos ni "p" ni "~ p"; "Q" y "~ q"; ni "r" y "~ r" unidos con un operador lógico disyuntivo. Por tanto, el valor de verdad de las proposiciones disyuntivas no es verdadero. Por lo tanto, afirma que el valor de verdad de la proposición conjuntiva es falso, ya que el valor de verdad de las proposiciones disyuntivas que están conectadas con un operador lógico conjuntivo en el CNF no es verdadero. Por tanto, toda la proposición no es una tautología.
Ejemplo-4: ((p → q) ≡ (~ p ∨ q))
((p → q) ≡ (~ p ∨ q)) Esta proposición se nos da
= ((~ p ∨ q) ≡ (~ p ∨ q)) Fórmula aplicada-11
= ((~ p ∨ q) ∧ (~ p ∨ q)) ∨ (~ (~ p ∨ q) ∧ ~ (~ p ∨ q)) Fórmula aplicada-16
= (~ p ∨ q) ∨ ~ (~ p ∨ q) Fórmula aplicada-19
= (~ p ∨ q) ∨ (p ∧ ~ q) Fórmula aplicada-8
= (~ p ∨ q ∨ p) ∧ (~ p ∨ q ∨ ~ q) Fórmula aplicada-7 (Esto es CNF)
Esta expresión está en la forma conjuntiva normal. Es así porque encontramos variables proposicionales y su negación están conectadas con un operador lógico disyuntivo dentro del corchete, y las proposiciones disyuntivas están conectadas con un operador lógico conjuntivo. En el CNF, encontramos "p" y "~ p" en la proposición disyuntiva del lado izquierdo y "q" y "~ q" en la proposición disyuntiva del lado derecho entre otras variables proposicionales. Dado que “p”y “~ p”, “q” y “~ q” están conectados con el operador lógico disyuntivo, el valor de verdad de la proposición disyuntiva del lado izquierdo y la proposición disyuntiva del lado derecho serían verdaderas incluso si la verdad -valor de una de las variables proposicionales es verdadero. Además, no importa cuál sería el valor de "q" con respecto a la proposición disyuntiva del lado izquierdo y "~ p" con respecto a la proposición disyuntiva del lado derecho. La razón es que “q”y “~ p” están conectados con sus respectivas variables proposicionales con disyunción. Dado que “p” “~ p” es verdadero en la proposición disyuntiva del lado izquierdo y m “q” “~ q” es verdadero en la proposición disyuntiva del lado derecho, el valor de verdad de las proposiciones disyuntivas sería verdadero. Dado que ambas proposiciones disyuntivas están unidas con conjunción y sus valores de verdad son verdaderos, el valor de verdad de toda la expresión es verdadero. Es así porque el valor de verdad de una proposición conjuntiva es verdadero cuando sus dos variables proposicionales son verdaderas. Por tanto, toda la expresión simbólica es una tautología.
1.16 Demostración de la validez de los argumentos
Para probar la validez de un argumento, necesitamos averiguar si la conclusión del argumento puede derivarse de sus premisas o no. Para hacerlo, hay un procedimiento de decisión que debemos adaptar conocido como "probar la validez del argumento". La prueba de validez es un procedimiento de decisión para determinar la validez o invalidez de un argumento. Probar la validez de un argumento es como resolver un rompecabezas para el que no habrá un modus operandi fijo o una estrategia. Tenemos que tratar cada argumento de manera diferente, ya que cada argumento requiere una estrategia diferente para averiguar si la conclusión dada se sigue de sus premisas o no. no. Para probar la validez de un argumento, necesitamos aplicar las fórmulas de derivación proposicionales mencionadas anteriormente. Estas fórmulas son las reglas evidentes por sí mismas. Usamos estas fórmulas para derivar la conclusión de las premisas. Probemos los siguientes argumentos simbólicos y averigüemos su validez.
Argumento-1
Premisa-1: a → b
Premisa-2: b → c
Premisa-3: a
Conclusión: c
Ahora, organice las premisas y la conclusión en una lista y averigüe si la conclusión puede derivarse de estas premisas aplicando fórmulas de derivación proposicionales.
1: a → b
2: b → c
3: a
Conclusión: c
4. a → c (de 1 y 2 aplicando la fórmula-13)
5. c (de 4 y 3 aplicando la fórmula-14)
Este argumento se prueba como un argumento válido.
Argumento-2
Premisa-1: a → ~ b
Premisa-2: ~ b → c
Premisa-3: c → d
Premisa-4: (a ∧ d) → e
Conclusión: a → e
Ahora, organice las premisas y la conclusión en una lista y averigüe si la conclusión dada se puede derivar de estas premisas aplicando fórmulas de derivación proposicionales.
1. a → ~ b
2. ~ b → c
3. c → d
4. (a ∧ d) → e
Conclusión: a → e
5. a → c (de 1 y 2 aplicando la fórmula-13)
6. a → d (de 5 y 3 aplicando la fórmula-13)
7. a → (a ∧ d) (de 6 aplicando la fórmula-20)
8. a → e (de 7 y 4 aplicando la fórmula-13)
Se demuestra que este argumento es un argumento válido.
Argumento-3
Premisa-1: a → b
Premisa-2: b → c
Premisa-3: b → d
Premisa-4: ~ d
Premisa-5: a ∨ b
Conclusión: c
Ahora, organice las premisas y la conclusión en una lista y averigüe si la conclusión dada se puede derivar de estas premisas aplicando fórmulas de derivación proposicionales.
1. a → b
2. b → c
3. b → d
4. ~ d
5. a ∨ b
Conclusión: c
6. ~ b (de 3 y 4 aplicando la fórmula-14)
7. ~ a (de 1 y 6 aplicando la fórmula-14)
8. b (de 5 y 7 aplicando la fórmula 21)
9. c (de 2 y 8 aplicando la fórmula 14)
Se demuestra que este argumento es un argumento válido.
Argumento-4
Premisa-1: a → b
Premisa-2: b → (c ∨ d)
Premisa-3: d → e
Premisa-4: e → f
Premisa-5: c → g
Premisa 6: a
Premisa-7: ~ g
Conclusión: f
Ahora, organice las premisas y la conclusión en una lista y averigüe si la conclusión dada se puede inferir de estas premisas aplicando fórmulas de derivación proposicionales.
1. a → b
2. b → (c ∨ d)
3. d → e
4. e → f
5. c → g
6. a
7. ~ g
Conclusión: f
8. a → (c ∨ d) (de 1 y 2 aplicando la fórmula-13)
9. c ∨ d (de 8 y 6 aplicando la fórmula-14)
10. ~ c (de 5 y 7 aplicando la fórmula-14)
11. d (de 9 y 10 aplicando la fórmula-21)
12. d → f (de 3 y 4 aplicando la fórmula-13)
13. f (de 12 y 11 aplicando la fórmula-14)
Este argumento se prueba como un argumento válido. Consideremos ahora los siguientes pasajes como argumentos. Cada argumento consta de premisas y una conclusión. Simbolizaremos las premisas y la conclusión del argumento utilizando los alfabetos y operadores lógicos en inglés. A partir de entonces, averiguaremos si la conclusión dada se deriva de las premisas o no. En resumen, averiguaremos la validez de los argumentos aplicándoles las fórmulas de derivación proposicional.
Argumento-5
Si un administrador toma una decisión importante, y si desea implementarla, entonces debe ser racional en su decisión. El administrador no toma una decisión importante. Es falso que el administrador sea racional en su decisión. Por lo tanto, el administrador no implementará su decisión.
Permitir a: un administrador toma una decisión importante.
yo — Ella quiere implementarlo.
r — Debe ser racional en su decisión.
1. (a ∧ i) → r
2. ~ a
3. ~ r
Conclusión: ~ i
4. ~ (a ∧ i) (de 1 y 3 aplicando la fórmula-14)
5. ~ a ∨ ~ i (de 4 aplicando la fórmula-8)
6. ~ i (de 5 y 2 aplicando la fórmula-21)
Se demuestra que este argumento es un argumento válido.
Argumento-6
Si la mayoría no está dispuesta a aceptar la decisión de la minoría, no puede haber democracia. Si la minoría no respeta los derechos de la mayoría, la mayoría no estará dispuesta a aceptar la decisión de la minoría. La minoría no respeta los derechos de la mayoría. Por tanto, no puede haber democracia.
Sea m: la mayoría está dispuesta a aceptar la decisión de la minoría.
d — Puede haber una democracia.
r — La minoría respeta los derechos de la mayoría.
1. ~ m → ~ d
2. ~ r → ~ m
3. ~ r
Conclusión: ~ d
4. ~ m (de 2 y 3 aplicando la fórmula-14)
5. ~ d (de 1 y 4 aplicando la fórmula-14)
Este argumento se prueba como un argumento válido.
1.17 Lógica de predicado
Ya discutimos la lógica simbólica en detalle. La lógica simbólica es una parte de la lógica de la oración donde una oración (sentencia) se considera como la unidad básica de un argumento. Mientras discutíamos la lógica simbólica, discutimos las variables proposicionales, las conectivas lógicas y el método tabular de verdad para determinar el valor de verdad de una proposición. También aclaramos el método del árbol de Beth, la forma normal conjuntiva y la forma normal disyuntiva para determinar el valor de verdad de proposiciones complejas y juzgar la validez de los argumentos. Además de estos temas, explicamos los métodos para probar la validez de los argumentos aplicando reglas de derivación proposicionales. Continuando con la sección anterior, en esta sección, deliberaremos sobre la lógica de predicados. Explicaremos el cuantificador universal y el cuantificador existencial. Discutiremos el método para traducir oraciones lógicas a la forma lógica de predicados considerando la semántica de las oraciones. También ilustraremos la oposición de proposiciones considerando proposiciones categóricas de lógica de predicados. Además, probaremos la validez de los argumentos adoptando reglas de derivación proposicionales.
1.18 ¿Qué es la lógica de predicados?
En la lógica de predicados, una proposición y su tema se toman en consideración al traducir una proposición en forma simbólica. Aquí, debemos considerar la calidad y la cantidad de una proposición mientras la traducimos en forma simbólica. El objetivo de la lógica de predicados es explicar la estructura lógica interna de una proposición mientras la traduce a una forma simbólica. Gottlob Frege (1848-1925), un filósofo alemán que se cree que es el fundador de la lógica de predicados y la filosofía analítica, escribe que la lógica oracional no expresa el concepto de una proposición con precisión cuando se traduce a lógica simbólica[62]. Por lo tanto, una oración de lógica simbólica debe considerar la calidad y cantidad de una proposición para transmitir correctamente el tema de la proposición. Esto ayudaría a determinar correctamente la validez de un argumento.
Frege explica la noción de "cuantificación" en su trabajo Concept Script (Begriffsschrift) (1879). Siguiendo a Frege, el profesor Alfred North Whitehead (1861-1947[63]) y Bertrand Russell (1872-1970) elaboran el trabajo sobre 'cuantificación' de la lógica de predicados en su manuscrito Principia Mathematica. Estos tratados destacan los defectos de la lógica oracional. En lógica oracional, una proposición se considera la unidad básica de un argumento. El tema de la proposición no se toma en consideración al traducirlo a forma simbólica. Por ejemplo,
Sita es bailarina, "p".
Sita no es una bailarina: "~ p".
Todas las mujeres son hermosas, "p".
No todas las mujeres son hermosas, "~ p".
En estos ejemplos, encontramos que "~p" representa dos proposiciones y "p" representa dos proposiciones. Aunque las dos proposiciones se simbolizan como "p", ambas tienen calidad afirmativa pero difieren en cantidad. Existe una situación similar con las proposiciones "~p". En este contexto, surge una pregunta: ¿es correcto simbolizar una proposición considerando solo su calidad e ignorando su cantidad? En la lógica oracional, cada proposición se simboliza como "p" o "m", o "s" o una letra minúscula del alfabeto inglés como variable proposicional. En este caso, consideramos la estructura de la proposición cuando simbolizamos la proposición. No consideramos el significado de la proposición para su simbolización. Por ejemplo, podemos simbolizar la proposición "Todos los cisnes son blancos" como "p" y "La hierba es verde" como "p". Aquí, "Todos los cisnes son blancos" y "La hierba es verde" son proposiciones afirmativas y se simbolizan como "p", pero no transmiten un significado similar. Además, la proposición "Algunos estudiantes son altos" se puede simbolizar como "p" y "Todos los estudiantes son solteros" también se puede simbolizar como "p". Estas dos proposiciones también se juzgan como proposiciones afirmativas, pero difieren entre sí en cuanto a sus significados. Es así porque, cuando la proposición "Algunos estudiantes son altos" se refiere a unos pocos estudiantes, la proposición "Todos los estudiantes son solteros" se refiere a todos los estudiantes. Además, cuando la primera proposición se refiere a la estatura de los estudiantes, la segunda proposición se refiere a la licenciatura de los estudiantes. Aunque estas dos proposiciones difieren significativamente entre sí, sin embargo, en la lógica de la oración, simbolizamos estas dos proposiciones como "p". En lógica oracional, consideramos la calidad (afirmativa o negativa) de una proposición solo mientras simboliza la proposición. Esto conduce a una situación crítica en la que, si consideramos una proposición afirmativa como "p" en un argumento independientemente de su cantidad (universal o particular), entonces el argumento puede parecer válido, pero no sería válido de hecho. Por ejemplo,
Todos los estudiantes son jugadores de fútbol.
Algunos nadadores son estudiantes.
Por lo tanto, algunos nadadores son jugadores de fútbol.
Este argumento consta de tres proposiciones: una premisa mayor, una premisa menor y una conclusión. Todas estas proposiciones son proposiciones afirmativas. En la lógica de la oración, simbolicemos la premisa mayor como "p", la premisa menor como "q" y la conclusión como "r". Entonces, podemos escribir
p
q
Por tanto, r.
Podemos escribir el argumento en forma de proposición simbólica como ((p ∧ q) → r). Ahora, los problemas no son ni "p" ni "q". El símbolo revela la estructura interna de la proposición (es decir, la cantidad de proposiciones). Además, los símbolos "p" y "q" no indican nada sobre el predicado de la proposición. Más bien, representan la proposición completa como tal. Debido a la falta de claridad en las proposiciones simbólicas de la premisa mayor y la premisa menor, la derivación de la conclusión de la premisa mayor y menor juntas conducirá a confusión y desconcierto. Dado que consideramos solo la estructura de la proposición, no el significado de la proposición, en la lógica de la oración, podemos terminar derivando una conclusión inválida de las premisas verdaderas. Para arreglar las lagunas de la lógica oracional, se introduce la lógica de predicados en el sujeto lógico. La lógica de predicados también se conoce como cálculo de predicados. La lógica de predicados considera la calidad y cantidad de una proposición mientras traduce la proposición en forma simbólica. El objetivo de la lógica de predicados es hacer que la estructura interna de la proposición sea correcta y vívida. En resumen, en la lógica de predicados, la calidad de una proposición (afirmativa o negativa) y la cantidad (universal o particular) se aclaran al traducirla en forma simbólica. En este sentido, la lógica de predicados ofrece información exacta y precisa sobre la estructura interna de la proposición. En la lógica de predicados, se le da importancia al predicado. Significa que necesitamos averiguar si el predicado afirma o niega al sujeto en la proposición y, además, si el predicado afirma al sujeto en parte o en su totalidad. Puede haber casos en los que el predicado de una proposición declare algo sobre dos sujetos diferentes de una proposición. Por ejemplo, Mario y María son profesores de las universidades gubernamentales de México. También hay situaciones en las que una proposición tiene dos predicados, y se refieren a un sujeto y afirman algo afirmativa o negativamente sobre él. Por ejemplo, Rogelio es un estudiante inteligente y sincera. Debido a estas características peculiares de las proposiciones, en la lógica de predicados, tanto el sujeto como el predicado se consideran propiedades de las proposiciones. En la lógica de predicados, una proposición se explica así con sus propiedades. Por ejemplo, "Todos los cisnes son blancos". Esta proposición se explica en la lógica de predicados como si hubiera algo que tuviera la propiedad de ser un cisne; luego, tiene la propiedad de ser blanco. Considere otro ejemplo: "Todos los estudiantes de lógica son inteligentes". Esta proposición en la lógica de predicados se analiza como si una persona (cosa) fuera un estudiante de lógica, entonces tiene la propiedad de ser inteligente. Tenga en cuenta que en la lógica de predicados, nos ocupamos de una cosa que tiene propiedad (es). La lógica de predicados proporciona más información sobre la proposición en comparación con la lógica de la oración. Sin embargo, la lógica de predicados toma prestadas muchas cosas de la lógica enunciativa. Por ejemplo, en lógica oracional, utilizamos constantes lógicas y conectivas lógicas mientras traducimos una proposición compuesta a la proposición simbólica. También en la lógica de predicados, usamos constantes lógicas y conectivas lógicas mientras traducimos proposiciones compuestas en proposiciones simbólicas. En lógica proposicional, para probar la validez de un argumento, usamos reglas de derivación proposicionales, etc. Usamos las reglas de derivación proposicionales en la lógica de predicados también para probar la validez de un argumento. Por lo tanto, no sería inapropiado decir que la lógica de predicados es una extensión y un avance de la lógica oracional. En la lógica de predicados, los siguientes símbolos se utilizan para traducir proposiciones en proposiciones simbólicas.
(i) Variables individuales: x, y, z,…
(ii) Constantes individuales para nombres propios: a, b, c, ...
(iii) Cuantificador universal: ∀x
(iv) Cuantificador existencial: ∃x
(v) Predicados: L, M, N,…
El símbolo "∀x" se transmite como "para todos los valores de x", y "∃x" se lee como "hay al menos una cosa x tal que". El cuantificador universal "x" se relaciona con las proposiciones categóricas A y E, mientras que el cuantificador existencial "x" se ocupa de las proposiciones categóricas I y O. Ahora, analicemos cuatro proposiciones categóricas A, E, I y O de la lógica de predicados y analicemos aquellas con ejemplos apropiados.
R: Todos los estudiantes de lógica son seres racionales.
E: Ningún estudiante de lógica es astronauta.
E: Algunos estudiantes de lógica son nadadores.
O: Algunos estudiantes de lógica no son jugadores de fútbol.
1.19 Cuantificador universal
El cuantificador universal se simboliza como "∀x". Se lee como "para todo x". El cuantificador universal "∀x" se utiliza en el caso de proposiciones A (universal afirmativo) y E (universal negativo). En el caso de las proposiciones A y E, todos los miembros del sujeto se toman en consideración al simbolizar las proposiciones. Con respecto a la proposición A, todos los miembros del sujeto tienen una cualidad o cosa sobre la que el predicado afirma, mientras que en el caso de la proposición E, todos los miembros del sujeto niegan una cualidad o cosa sobre la que el predicado afirma. Por ejemplo, "Todos los estudiantes de lógica son seres racionales". Esta es una propuesta A. Ahora, simbolicémoslo en la lógica de predicados.
A: Todos los estudiantes de lógica son seres racionales.
= (Sea lo que sea x) (Si x es un estudiante de lógica, entonces es un ser racional)
= (∀x) (Si x es L entonces x es R)
= (∀x) (Lx → Rx)
En este caso, hemos considerado L para "estudiante de lógica" y R para "ser racional", y la proposición "si entonces" se simboliza con "implicación" conectiva lógica.
Un ejemplo de la proposición E es "Ningún estudiante de lógica es astronauta". Ahora, simbolizaremos la proposición en la lógica de predicados.
E: Ningún estudiante de lógica es astronauta.
= (Sea lo que sea x) (Si x es un estudiante de lógica, entonces x no es un astronauta)
= (∀x) (Si x es L entonces x no es una A)
= (∀x) (Lx → ~ Ax)
En este caso, hemos tomado L para "estudiante de lógica" y A para "astronauta". La palabra no se simboliza como "~".
1.20 Cuantificador existencial
El cuantificador existencial se simboliza como "∃x". Se lee como "para alguna x". El cuantificador existencial "x" se usa para proposiciones I (afirmativa particular) y O (negativa particular). En el caso de las proposiciones I y O, al menos un miembro del sujeto se toma en consideración mientras simboliza las proposiciones. En el caso del cuantificador existencial, una función proposicional afirma que al menos una instancia de sustitución verdadera existe como verdadera. Significa que estamos sustituyendo una constante individual por su variable individual Con respecto a la proposición I, al menos un miembro del sujeto tiene una cualidad o cosa sobre la que el predicado dice, mientras que en el caso de la proposición O, al menos un miembro del sujeto niega una cualidad o una cosa sobre la que el predicado establece. Por ejemplo, "Algunos estudiantes de lógica son nadadores". Esta es una propuesta de I. Ahora, simbolicémoslo en la lógica de predicados.
I: Algunos estudiantes de lógica son nadadores.
= (Hay algo x) (Esta x es un estudiante y esta x es un nadador)
= (∃x) (Esta x es una S y esta x es M)
= (∃x) (Sx ∧ Mx)
En este caso, hemos considerado S para "estudiante" y M para "nadador", y la proposición se simboliza con la conjunción conectiva lógica. Ahora, consideraremos una proposición O y simbolizaremos la proposición en la lógica de predicados.
O: Algunos estudiantes de lógica no son jugadores de fútbol.
= (Hay algo x) (Esta x es un estudiante y esta x no es un jugador de fútbol)
= (∃x) (Esta x es una S y esta x no es una C)
= (∃x) (Sx ∧ ~ Cx)
En esta proposición simbólica, hemos tomado S para "estudiante" y C para "jugador de fútbol". La palabra no se simboliza como "~".
1.21 Proposición atómica
Una proposición atómica es aquella que no se combina con ninguna otra proposición, y no se puede dividir en otras proposiciones simples. Las proposiciones atómicas se conocen como proposiciones elementales y proposiciones simples. Ejemplos de proposiciones atómicas son: Rogelio es un buen chico, el autor de ética es un hombre alto, etc. Estas proposiciones no se combinan con ninguna otra proposición. No contienen ningún conectivo lógico, como "y", "uno o" y "si entonces" para determinar su función de verdad. La parte del sujeto de una proposición atómica es un nombre propio (Rogelio) o una descripción definida (el autor de de ética) del sujeto. En la lógica de predicados, se entiende que el sujeto de una proposición debe ser una cosa o una persona que tiene una cualidad sobre la que el predicado está expresando. Así, la simbolización de una proposición atómica en la lógica de predicados se lleva a cabo de una manera única donde se toman en consideración tanto la calidad como la cantidad de la proposición. Usamos alfabetos pequeños como a, b, c, etc., para una persona o una cosa, y letras mayúsculas como A, B, C, etc., para la calidad del tema. El símbolo de calidad se usa a la izquierda de la persona o cosa.
Por ejemplo:
Ejemplo 1
Rogelio es un buen chico.
= m es una G
= G m
En esta proposición simbólica, "m" significa Rogelio y "G" significa "buen chico".
Ejemplo 2
María es cantante.
= s es una N
= Ns
En esta proposición simbólica, "s" significa María y "N" significa "cantante".
Ahora, consideremos una proposición compuesta donde un sujeto tiene dos cualidades, y simbolicémosla en la lógica de predicados.
Ejemplo 3
Mira es cantante y bailarina.
= m es una S y m es una D
= Sm ∧ Dm
En esta proposición simbólica, "m" significa Mira, "S" significa "cantante" y "D"
significa "bailarina".
Ejemplo 4
Mita es jugadora de bádminton y escritora.
= m es una B y m es una W
= Bm ∧ Wm
En esta proposición simbólica, "m" significa Mita, "B" significa "bádminton
jugador” y W significa "escritor".
1.22 Oposición de proposición
Discutimos la oposición de proposiciones como parte de la lógica oracional. Tomamos prestadas las reglas y condiciones de la oposición de proposiciones y las usamos en la lógica de predicados. Tomamos prestadas las proposiciones A, E, I y O de la lógica enunciativa para explicarlas en la lógica de predicados. En la lógica de predicados se encuentran cuatro formas de oposición de proposiciones que están relacionadas con las proposiciones atómicas A, E, I y O. Estos son:
(i) Subalternación
(ii) Contrario
(iii) Subcontrario
(iv) Contradictorio
En la figura siguiente las proposiciones A y E están relacionadas entre sí en relación contraria, y las proposiciones A e I, y E y O están relacionadas entre sí en relación de subalternación. Las proposiciones I y O tienen la relación subcontraria. Además, las proposiciones A y O, y E e I están relacionadas entre sí en una relación contradictoria. Las proposiciones categóricas A, E, I y O se tratan con la cantidad y calidad de las proposiciones. Las proposiciones A y E están simbolizadas en cuantificadores universales, mientras que las proposiciones I y O están simbolizadas en cuantificadores existenciales. Ahora, simbolicemos las proposiciones A, E, I y O en la lógica de predicados con el sujeto X y el predicado Y.
 13.48.33.png)
Oposición de propuestas
 13.50.36.png)
1.23 Traducción de proposiciones lógicas a lógica de predicados
A diferencia de la lógica oracional, en la lógica de predicados, tanto la calidad como la cantidad de la proposición se toman en consideración al simbolizarla. El objetivo de la lógica de predicados es revelar la estructura interna de la proposición a través de su forma simbólica. A partir de ahora, hemos discutido los métodos para simbolizar proposiciones atómicas y proposiciones compuestas en la lógica de predicados. Pero en el discurso lingüístico, es posible que no siempre encontremos proposiciones simples o compuestas. Más bien, hay ocasiones en las que las proposiciones no se encuentran en una forma lógica estándar. Para simbolizar estas proposiciones en la lógica de predicados, necesitamos reducir estas proposiciones a la forma lógica estándar y necesitamos identificar la calidad y cantidad de estas proposiciones. A continuación, aclararemos algunos ejemplos de este tipo de proposiciones para su referencia, comprensión y comprensión. discernimiento. Por ejemplo,
Ejemplo 1
Ninguno de los ingenieros civiles de la ciudad pudo salvar el paso elevado.
= Ningún ingeniero civil en la ciudad es una persona que pueda salvar el paso elevado.
= (Cualquiera que sea x) (Si x es un ingeniero civil en la ciudad, entonces x es una persona que
no pudo salvar el paso elevado)
= (∀x) (Cx → ~ Fx)
Ejemplo 2
No a todos los estudiantes les gusta la lógica.
= A algunos estudiantes no les gusta la lógica.
= (Hay algo x) (Esta x es un estudiante y a x no le gusta la lógica)
= (∃x) (Sx ∧ ~ Lx)
Ejemplo 3
Solo los profesores son doctores.
= Todos los que son doctores son profesores.
= (Cualquiera que sea x) (Si x es un doctorado, entonces x es un profesor)
= (∀x) (Dx → Px)
En el discurso lingüístico, también se encuentra que las proposiciones tienen un sujeto y un predicado, y el sujeto y el predicado tienen más de una cualidad. Para simbolizar este tipo de proposición en la lógica de predicados, necesitamos averiguar la calidad y cantidad de la proposición. Por ejemplo,
Ejemplo 1
Las chicas que nadan son fuertes.
= (Cualquiera que sea x) (Si x es una niña y x es un nadador, entonces x es fuerte)
= (∀x) ((Gx ∧ Mx) → Sx)
En esta proposición simbólica, G significa "niña", M significa "nadador" y S
significa "fuerte".
Ejemplo 2
Los niños que juegan al bádminton son fuertes y activos.
= (Cualquiera que sea x) (Si x es un niño y x juega bádminton, entonces x es fuerte y
x está activo)
= (∀x) ((Bx ∧ Nx) → (Sx ∧ Ax))
En esta proposición simbólica, B significa "niño", N significa "bádminton", S
significa "fuerte" y A significa "activo".
Ejemplo 3
Es falso que algunos estudiantes sean analfabetos.
= ~ (Hay algo x) (Esta x es un estudiante y esta x es analfabeta)
= ~ (∃x) (Sx ∧ Ix)
En esta proposición simbólica, S significa "estudiante" y I representa "analfabeto".
También hay proposiciones que constan de más de una cosa (o una persona) y un predicado. Para simbolizar este tipo de proposición en la lógica de predicados, necesitamos averiguar los nombres de las cosas o personas y predicados usados en la proposición. Por ejemplo,
Ejemplo 1
A todos les gusta algo.
= (Sea lo que sea x) (Si x es una persona, (hay algo y, y es una cosa), entonces
x le gusta y)
= (∀x) (Px → (∃y) Lxy)
En esta proposición simbólica, "todos" se reduce a "todas las personas". Por tanto, se representa mediante un cuantificador universal. Tomamos la variable "x" para representar a "todas las personas". La palabra "algo" se representa en cuantificador existencial. En este caso, tomamos la variable "y" para representar "algo". La palabra "me gusta" es un predicado que conecta a "todos" con "algo". Como resultado, la proposición establece que si hay una persona y hay una cosa, entonces a la persona le gusta esa cosa.
Ejemplo 2
Alguien ama a todos.
= (Hay algo x) (Esta x es una persona y (sea lo que sea y, si y es una
persona entonces x ama y))
= (∃x) (Px ∧ (∀y) (Py → Lxy))
En esta proposición simbólica, "alguien" se reduce a "una persona". Por tanto, se simboliza en cuantificador existencial. La palabra "todos" se reduce a "todas las personas" y se representa en un cuantificador universal. Para el cuantificador universal y el cuantificador existencial, hemos tomado dos variables separadas, x e y, respectivamente. La palabra "amor" es el predicado que conecta "una persona" con "cada persona". Como resultado, esta proposición establece que hay una persona y si hay otras personas, entonces una persona ama a todas las demás.
Ejemplo 3
Todo el mundo ama a alguien.
= (Cualquiera que sea x) (Si x es una persona, entonces (hay algo y, esta y es una
persona y x ama a esta persona))
= (∀x) (Px → (∃y) (Py ∧ Lxy))
En esta proposición simbólica, "alguien" se reduce a "una persona", por lo que se representa a través del cuantificador existencial. La palabra "todos" se reduce a "todas las personas" y se representa a través de un cuantificador universal. Para el cuantificador universal y el cuantificador existencial, hemos tomado dos variables separadas, x e y, respectivamente. La palabra "amor" es un predicado que conecta "todas las personas" con "una persona". Por tanto, esta proposición establece que si hay una persona, entonces hay otra persona y todas y cada una de las personas aman a esa persona.
1.24 Demostración de la validez de los argumentos
En lógica oracional, explicamos las técnicas y los procedimientos para probar la validez de los argumentos simbólicos mediante la aplicación de fórmulas de derivación proposicionales. Las fórmulas de derivación proposicionales se consideran reglas evidentes por sí mismas. Usamos estas fórmulas en la lógica de predicados para probar la validez de argumentos simbólicos. Para nuestra conveniencia y referencia inmediata, mencionamos las fórmulas de derivación proposicionales para probar la validez de los argumentos.
 13.58.27.png)
Junto con estas fórmulas, necesitamos otras cuatro reglas para probar la validez de los argumentos en la lógica de predicados. Estas reglas son:
Creación de instancias universal (UI)
Generalización universal (UG)
Instanciación existencial (EI)
Generalización existencial (EG)
La expresión "instanciación universal" se abrevia como UI. La rule UI expresa que en una proposición, cualquier cosa que se predique (ya sea afirmativa o negativamente) universalmente a una clase, puede predicarse (ya sea afirmativa o negativamente) a todos sus miembros de la clase. Por ejemplo, si "Todos los cuervos son negros" es verdadero, entonces "Cuervo x es negro", "Cuervo y es negro", "Cuervo z es negro", etc., también son verdaderos. Además, si "Ningún cisne es negro" es cierto, entonces "El cisne x no es negro", "El cisne y no es negro" y "El cisne z no es negro" también son verdaderas. La expresión "generalización universal" se abrevia como UG. La regla UG establece que si una proposición dada es verdadera para cualquier cosa o persona, entonces aplicando la regla de inferencia, a partir de esta proposición, podemos inferir la proposición válida universal. Por ejemplo, si "La suma de los tres ángulos interiores de un triángulo es igual a dos ángulos rectos" es verdadera, entonces "La suma de los tres ángulos interiores de todos los triángulos es igual a dos ángulos rectos" también es verdad. La expresión "instanciación existencial" se abrevia como EI. La regla EI expresa que en una proposición todo lo que se predica (ya sea afirmativa o negativamente), particularmente a una clase, puede predicarse (ya sea afirmativa o negativamente) al menos a un miembro de la clase. Por ejemplo, si "Algunos estudiantes son nadadores" es cierto, entonces al menos un estudiante dice que “Rogelio es un nadador" también es cierto. Además, si "Algunos estudiantes no son jugadores de fútbol" es cierto, entonces al menos un estudiante dice que “José no es un jugador de fútbol" también es cierto. La expresión "generalización existencial" se abrevia como EG. La regla EG establece que si una proposición dada es verdadera para cualquier cosa o persona, entonces aplicando la regla de inferencia, a partir de esta proposición, podemos inferir la cuantificación existencial de la proposición. Por ejemplo, si "La suma de los tres ángulos interiores de un triángulo es igual a dos ángulos rectos" es verdadera, entonces "La suma de los tres ángulos interiores de todos los triángulos es igual a dos ángulos rectos" también es verdad. Ahora, probemos la validez de los siguientes argumentos en la lógica de predicados.
Ejemplo 1
Todos los profesores son aprendices.
Todos los investigadores son profesores.
Por tanto, todos los investigadores son aprendices.
La traducción simbólica de este argumento es la siguiente.
(∀x) (Tx → Lx)
(∀x) (Rx → Tx)
Por lo tanto, (∀x) (Rx → Lx)
En este argumento, T significa "maestro", L significa "aprendiz" y R significa "investigador". Al traducir la proposición en forma simbólica, hemos tenido en cuenta la calidad y cantidad de todas las proposiciones del argumento. Podemos probar la validez de este argumento de dos formas. Primero, aplique la regla de UI a todas las premisas del argumento, ya que son proposiciones afirmativas universales (proposiciones A). Podemos reemplazar una constante individual, digamos "a" con la variable "x". Por tanto, no necesitamos mencionar el cuantificador en el argumento. Una vez que formulamos el argumento con constante individual, podemos aplicar las fórmulas de derivación proposicionales para probar la validez del argumento. Al hacerlo, estamos reduciendo el argumento de lógica de predicados a un argumento de lógica de oración.
1. (Ta → La)
2. (Ra → Ta)
Conclusión (Ra → La)
3. (Ra → La) (de 2 y 1 aplicando la fórmula-13)
Este argumento se prueba como un argumento válido.
En segundo lugar, necesitamos reducir el cuantificador de las premisas del argumento una por una utilizando las reglas UI y EI, como se exige. Al final de este proceso, encontramos que el argumento de la lógica de predicados se reduce a la forma de lógica enunciativa. Luego, aplicamos las fórmulas de derivación proposicionales para probar la validez del argumento. A partir de entonces, traducimos la proposición lógica oracional (conclusión del argumento) en forma de proposición lógica predicada utilizando las reglas UG y EG según lo exigido.
El argumento anterior se prueba de la siguiente manera.
1. (∀x) (Tx → Lx)
2. (∀x) (Rx → Tx)
Conclusión (∀x) (Rx → Lx)
3. (Ta → La) (desde 1 usando la interfaz de usuario)
4. (Ra → Ta) (desde 2 usando la interfaz de usuario)
5. (Ra → La) (de 2 y 1 aplicando la fórmula-13)
6. (∀x) (Rx → Lx) (de 5 usando UG)
Este argumento se prueba como un argumento válido.
Ejemplo 2
1. (∀x) (Ax → Bx)
2. (∃x) (Ax ∧ Cx)
Por lo tanto, (∃x) Bx
Al aplicar el primer método, estamos probando la validez del argumento.
3. (Aa → Ba)
4. (Aa ∧ Ca)
Conclusión Ba
5. Aa (de 2 aplicando la fórmula-20)
6. Ca (de 2 aplicando fórmula-20)
7. Ba (de 1 y 3 aplicando la fórmula 14)
Este argumento se prueba como un argumento válido.
Ahora, aplicaremos el segundo método para probar la validez del argumento.
1. (∀x) (Ax → Bx)
2. (∃x) (Ax ∧ Cx)
Conclusión, (∃x) Bx
3. (Aa → Ba) (de 1 usando la interfaz de usuario)
4. (Aa ∧ Ca) (de 2 usando EI)
5. Aa (de 4 aplicando la fórmula 20)
6. Ca (de 4 aplicando fórmula-20)
7. Ba (de 3 y 5 aplicando la fórmula 14)
8. (∃x) (Bx) (desde 7 usando EG)
Este argumento se prueba como un argumento válido.
1.25 Silogismo puro y mixto
En el módulo anterior, discutimos las cuatro figuras y los posibles modos de silogismo. Explicamos las reglas del silogismo y, aplicando las reglas, probamos todos los modos posibles del silogismo. Mencionamos los nombres de los estados de ánimo válidos sobre las cuatro figuras del silogismo. Discutimos las similitudes y diferencias entre la falacia formal y la falacia material, y aclaramos algunas de las falacias informales. Aquí discutiremos la naturaleza y tipos de silogismo puro, la diferencia entre silogismo puro y silogismo mixto, y tipos de silogismo mixto. Describiremos “sorites” y “entimemas” con ejemplos adecuados. Además, explicaremos el "dilema" y las formas del dilema con ejemplos. El silogismo es de dos tipos: silogismo puro y silogismo mixto. En el caso del silogismo puro, todas las proposiciones constituyentes (premisa mayor, premisa menor y conclusión) tienen la misma relación. Por ejemplo, si todas las proposiciones son categóricas, el silogismo se considera un silogismo categórico puro. Si todas las proposiciones son hipotéticas, el silogismo se considera un silogismo hipotético puro. Si todas las proposiciones son disyuntivas, el silogismo se considera un silogismo disyuntivo puro. Por lo tanto, tenemos tres tipos de silogismo puro: silogismo categórico puro, silogismo hipotético puro y silogismo disyuntivo puro.
A diferencia del silogismo puro, las proposiciones constituyentes de un silogismo mixto no tienen la misma relación. El silogismo mixto es de tres tipos: categórico hipotético, categórico disyuntivo y dilema. En el caso del silogismo categórico hipotético, la premisa principal es una proposición hipotética; la premisa menor y la conclusión son proposiciones categóricas. En el caso del silogismo categórico disyuntivo, la premisa principal es una proposición disyuntiva; la premisa menor y la conclusión son proposiciones categóricas. En el caso de un dilema, la premisa principal es una proposición compuesta hipotética. La premisa menor es una proposición disyuntiva. La conclusión es una proposición categórica o disyuntiva. El siguiente dibujo muestra tipos de silogismo.
Tipos de silogismo
 12.11.11.png)
1.26 Silogismo categórico puro
Un silogismo categórico puro acepta todas las reglas y normas del silogismo formal, como ya se discutió. Es una inferencia deductiva mediata. Consiste en tres proposiciones categóricas, a saber, premisa mayor, premisa menor y conclusión, y tiene tres términos, a saber, término mayor, término menor y término medio. A continuación se muestra un ejemplo de silogismo categórico puro.
A: Todos los estudiantes de lógica son seres inteligentes. (Premisa principal)
I: Algunos jugadores de críquet son estudiantes de lógica. (Premisa menor)
I: Por lo tanto, algunos jugadores de críquet son seres inteligentes. (Conclusión)
Este silogismo es válido porque corresponde a la primera figura del silogismo y satisface todas las reglas silogísticas. Se llama DARII. En este silogismo, se encuentran tres términos, a saber, término mayor, término menor y término medio. En la premisa principal, el término medio (es decir, estudiantes de lógica) y el término principal (es decir, seres inteligentes) concuerdan entre sí. En la premisa menor, término medio y término menor (es decir, jugadores de críquet) concuerdan entre sí. En conclusión, tanto los términos mayores como los menores concuerdan entre sí. Debido a la concordancia entre tres términos, la conclusión derivada de dos premisas se juzga como una proposición verdadera en este silogismo. En un silogismo categórico puro, todo lo que se niega o se afirma de una clase entera se negaría o se afirmaría de cualquier parte de ella.
En palabras de Aristóteles, se conoce como “Dictum de omni et nullo”. Este dicho se aplica solo a la primera figura del silogismo, ya que la primera figura del silogismo se considera la figura perfecta del silogism. Salvo la primera figura, el resto de figuras del silogismo no se consideran figuras perfectas del silogismo. Las razones son, como dijo Aristóteles, la proposición afirmativa universal "A" se encuentra en la conclusión de un silogismo válido (es decir, BARBARA) de la primera figura sola, que no se encuentra en otras figuras de silogismos válidos. Además, las proposiciones A, E, I, O se encuentran como una conclusión de estados de ánimo válidos de la primera figura (es decir, AAA, EAE, AII, EIO), que no se encuentran en otras figuras de silogismo.
1.27 La máxima de todos y ninguno
Con respecto al "Dictum de omni et nullo", Aristóteles sostiene que en un silogismo categórico puro, para cada proposición, lo que se predica (o no se predica) de un grupo se predica (o no se predica) de los miembros contenidos en ese es lo que es cierto para una determinada clase, lo es para los miembros de esa clase, y lo que no es cierto para una determinada clase, no lo es para los miembros de esa clase. Por ejemplo, si el color blanco es verdadero para todos los cisnes, entonces el color blanco debe ser verdadero para algunos miembros de la clase "cisne". Además, si el color amarillo no es cierto para todos los cuervos, entonces el amarillo no será cierto para algunos miembros de la clase "cuervo".
Un ejemplo de "Dictum de Omni et nullo"
Ningún hombre es un ser perfecto.
José es un hombre.
Por tanto, José no es un ser perfecto.
En este argumento, se afirma que los hombres (es decir, una clase) no son seres perfectos. José es un hombre que pertenece a la clase de "hombres" y, por tanto, José no es un ser perfecto. Este argumento afirma que todo lo que no es cierto para todos los hombres no debe serlo para José, ya que un miembro individual pertenece a la clase de "hombres".
Otro ejemplo de "Dictum de omni et nullo"
Los hombres son seres racionales.
Sócrates es un hombre.
Por tanto, Sócrates es un ser racional.
En este argumento, se afirma que los hombres (es decir, una clase) son seres racionales. Sócrates es un hombre que pertenece a la clase de los hombres ”. Por tanto, Sócrates es un ser racional. Este argumento establece que todo lo que es cierto para todos los hombres debe serlo para Sócrates, ya que un miembro individual pertenece a la clase de "hombres".
1.28 Entimemas
En nuestra vida diaria, formulamos y compartimos muchos argumentos con los oyentes en forma de inferencia deductiva mediata (silogismo). Mientras comunicamos los argumentos a los oyentes, no declaramos todas las proposiciones del argumento explícitamente, ya que se cree que será redundante enunciar las proposiciones verdaderas triviales y conocidas a los oyentes de un argumento. Sin embargo, el hablante tiene la intención de que el oyente pueda insertar la proposición verdadera trivial en el argumento de manera apropiada, y el oyente llevará a cabo esta tarea considerando la intención del hablante y el contexto del argumento. Esto se llama entimema. En pocas palabras, cuando un argumento carece de una de sus proposiciones, el oyente entiende la proposición no declarada (puede ser una premisa o una conclusión) basándose en la intención del hablante y el contexto del argumento, se conoce como un entimema. Este fenómeno de una discusión surge cuando un hablante comparte sus ideas parciales o incompletas con los oyentes y expresa sus puntos de vista sobre algo con vehemencia. Los entimemas se tratan como retórica, y la retórica es más poderosa y vigorosa cuando se comunica a través de un lenguaje en comparación con un argumento que se expresa en detalle con sus proposiciones constituyentes.
Un ejemplo de entimema
Todos los políticos son mentirosos.
Por tanto, Raul es una mentiroso.
Este argumento (silogismo) está incompleto porque solo tenemos dos proposiciones: una premisa y una conclusión. Necesitamos justificar la conclusión agregando una premisa tácita y faltante al argumento. Una vez que agregamos la premisa tácita al argumento, podemos probar el silogismo aplicando todas las reglas silogísticas y averiguar si el silogismo se considera un silogismo válido o no. El oyente agrega fácilmente la premisa perdida (premisa tácita) al argumento de su conocimiento y comprensión sobre los políticos y sus discursos públicos. El argumento completo (silogismo) aparecería como:
Todos los políticos son mentirosos. (Premisa mayor)
Raul es político. (Premisa menor)
Por tanto, Raul es un mentiroso. (Conclusión)
La proposición categórica “Raul es un político" se agrega al silogismo como premisa menor para derivar la conclusión. Esto se debe a que, en un silogismo, la conclusión se deriva de dos premisas al tomarlas juntas. Este silogismo tiene proposiciones categóricas A, I, I. Corresponde a la primera figura del silogismo en función de la posición de su término medio. Satisface todas las reglas silogísticas. Por lo tanto, es un silogismo válido tener AII un estado de ánimo válido llamado DARII. Los entimemas son de tres tipos: el entimema de primer orden, el entimema de segundo orden y el entimema de tercer orden. Estos tipos de entimemas se determinan en función de la proposición no declarada que falta en el argumento. En un argumento, si se mencionan la premisa menor y la conclusión, y la premisa mayor no se establece, pero se entiende implícitamente, se conoce como entimema de primer orden. De manera similar, en un argumento, si se mencionan la premisa mayor y la conclusión, y no se establece la premisa menor, pero se entiende implícitamente, se conoce como un entimema de segundo orden. Además, en un argumento, si se mencionan las premisas mayores y menores, y la conclusión no se establece, pero se entiende implícitamente, se denomina entimema de tercer orden.
Un ejemplo del entimema de primer orden
Todo nativo de México es ciudadano de México. (El oyente agrega esta proposición más adelante para el argumento)
Raul es originario de México.
Por lo tanto, Raul es ciudadano de México.
En este silogismo, la premisa principal no fue establecida por el hablante, pero el oyente la entiende implícitamente como "Todo nativo de México es ciudadano de México". Este silogismo corresponde a la primera figura del silogismo basado en su posición de término medio en las premisas. Se compone de proposiciones categóricas A, I, I. No viola ninguna regla silogística. Por tanto, es un silogismo válido de la primera figura denominada DARII.
Un ejemplo del entimema de segundo orden
Todos los estudiantes son personas educadas.
Todos los estudiantes de pregrado son estudiantes. (El oyente agrega esta proposición más adelante al argumento)
Por lo tanto, todos los estudiantes universitarios son personas educadas.
En este silogismo, la premisa menor no fue expresada por el hablante, pero el oyente la entendió implícitamente al considerar la intención del hablante y el contexto del argumento, como "Todos los estudiantes de pregrado son estudiantes". Este silogismo corresponde a la primera figura del silogismo basado en su posición de término medio en las premisas. Se compone de proposiciones categóricas A, A, A. Satisface todas las reglas silogísticas. Por tanto, es un silogismo válido de la primera figura llamada BARBARA.
Un ejemplo del entimema de tercer orden
Ningún verdadero mexicano es un pueblo rígido de mentalidad religiosa.
Algunos precios de los templos son rígidos para personas de mentalidad religiosa.
Por lo tanto, algunos precios de los templos no son verdaderos mexicanos. (El oyente agrega esta proposición más adelante al argumento)
En este silogismo, el orador no enunció la conclusión, pero el oyente la entendió al considerar la intención del orador y el contexto del argumento, como "Algunos precios de los templos no son verdaderos mexicanos”. Este silogismo corresponde a la segunda figura del silogismo basado en su posición de término medio en las premisas. Comprende proposiciones categóricas E, I, O. Satisface todas las reglas silogísticas. Por tanto, es un silogismo válido de la segunda figura denominada FESTINO. Hay ciertos casos en los que un hablante comparte dos premisas con el oyente, que son proposiciones categóricas negativas (es decir, E y O) o proposiciones categóricas particulares (es decir, I y O), el oyente no podrá derivar ninguna conclusión de estas dos. local. Si el oyente intenta derivar la conclusión no declarada del argumento, el argumento se consideraría un silogismo inválido, ya que no satisfará algunas de las reglas silogísticas. Por tanto, a partir de dos proposiciones categóricas negativas y dos proposiciones categóricas particulares, no se puede inferir ninguna conclusión (entimema de tercer orden).
1.29 Sorites
Un silogismo categórico consta de tres proposiciones: dos premisas y una conclusión. La conclusión de un silogismo se extrae de dos premisas considerándolas juntas. A diferencia del silogismo, un sorites requiere más de tres proposiciones para inferir la conclusión. En resumen, un sorites consta de más de tres proposiciones. La última proposición de los sorites se conoce como conclusión, y el resto de las proposiciones han tratado las premisas y/o conclusiones en función de sus posiciones en el argumento. Un sorites no se considera un silogismo, sino una cadena de silogismos categóricos. En sorites, todo el argumento es válido cuando los silogismos constituyentes se tratan como válidos. Las características más destacadas de un sorites son las siguientes: consta de más de tres premisas y la última proposición se considera una conclusión. Cada término de un silogismo constituyente de la cadena de silogismos categóricos aparece sólo dos veces. Además, algunas de las premisas y/o conclusiones se expresan entimemáticamente. La premisa no declarada y/o la conclusión del argumento deben agregarse al silogismo constituyente de la cadena de silogismos para llegar a la conclusión deseada. Al probar la validez de un sorites, debemos considerar las premisas y/o conclusiones no declaradas o faltantes de todo el argumento.
Un ejemplo de sorites
Todas las aves son criaturas voladoras. (Proposición-1)
Algunas especies emplumadas son aves. (Proposición-2)
Todas las especies emplumadas son animales bípedos.
En este ejemplo, se nos dan tres proposiciones categóricas. Ahora, necesitamos averiguar si estas tres proposiciones categóricas deben ser consideradas como premisa-1, premisa-2 y conclusión o no. Tras un examen, se encuentra que la última proposición no está vinculada a las otras dos proposiciones. Por tanto, no se consideraría como una conclusión del argumento. Entonces, necesitamos agregar una proposición después de la segunda proposición y antes de la última proposición. Es decir, "Algunas especies emplumadas son criaturas voladoras". Esta proposición se infiere considerando una regla silogística que establece que cada término debe aparecer dos veces en un silogismo, y el término medio debe establecer un vínculo entre el término mayor y el término menor para sacar una conclusión de un argumento. Entonces, la proposición "Algunas especies emplumadas son criaturas voladoras" se trata como un entimema de tercer orden. También se trata como una conclusión cuando consideramos la proposición 1 y la proposición 2 del argumento. Después de agregar la proposición "Algunas especies emplumadas son criaturas voladoras" al argumento, se encuentra que la última proposición no debe considerarse como una conclusión de los sorites. Las razones son que obtenemos un nuevo término animales bípedos en la parte del predicado de la proposición que no aparece dos veces en el argumento. Además, en consideración de las proposiciones “Algunas especies emplumadas son criaturas voladoras” y “Todas las especies emplumadas son animales bípedos”, encontramos un término intermedio (es decir, especies emplumadas) que se conecta con “animales bípedos” por un lado, y criaturas voladoras por otra parte. Como resultado, nos ayuda a sacar una conclusión, es decir, algunos animales bípedos son criaturas voladoras. Ahora, si consideramos el argumento completo, encontramos que el argumento consta de cinco proposiciones categóricas. La última proposición, "Algunos animales bípedos son criaturas voladoras", se considera una conclusión y las proposiciones anteriores se consideran premisas. Sin embargo, la proposición "Algunas especies emplumadas son criaturas voladoras" se considera tanto una premisa como una conclusión. Se considera una conclusión cuando consideramos la proposición 1 y la proposición 2 del argumento. Se trata como una premisa cuando consideramos que la proposición "Todas las especies emplumadas son animales bípedos" es una premisa, y "Algunos animales bípedos son criaturas voladoras" es una conclusión. En este caso, la conclusión de los sorites es un entimema de tercer orden, que no se declaró explícitamente en el argumento dado. Este sorites consta de dos silogismos de la siguiente manera:
Todas las aves son criaturas voladoras. (Proposición-1)
Algunas especies emplumadas son aves. (Proposición-2)
Algunas especies emplumadas son criaturas voladoras. (Proposición-3 y conclusión)
Todas las especies emplumadas son animales bípedos. (Proposición-4)
Por tanto, algunos animales bípedos son criaturas voladoras. (Conclusión)
Ahora, necesitamos probar estos sorites para averiguar si son sorites válidos o no. Al considerar la proposición-1, la proposición-2 y la proposición-3, encontramos que la proposición-1 y la proposición-2 se consideran la premisa principal y la premisa menor, respectivamente, y la proposición-3 es una conclusión válida. Es así porque la conclusión se extrae de las dos premisas al tomarlas juntas sin violar ninguna regla silogística. El modo válido del silogismo es AII, y corresponde a la primera figura del silogismo. Este silogismo válido se llama DARII. Este silogismo es uno de los componentes de las salidas. La razón es que además de este silogismo, encontramos otro silogismo cuando consideramos la proposición-3, la proposición-4 y la conclusión (última proposición) de los sorites. En este silogismo, la proposición-3 y la proposición-4 se consideran como premisa mayor y premisa menor, respectivamente. La conclusión del silogismo se infiere de la proposición-3 y la proposición-4 al tomarlas juntas. Este silogismo corresponde a la tercera figura y satisface todas las reglas silogísticas. El modo válido del silogismo es IAI, y se llama DISAMIS. La proposición "Algunos animales bípedos son criaturas voladoras" se trata como la conclusión del segundo silogismo y también como conclusión de los sorites.
Otro ejemplo de sorites
Todos los estudiantes son personas educadas.
Todas las personas educadas son nadadores.
Ningún animal cuadrúpedo es una persona educada.
Por lo tanto, ningún animal cuadrúpedo es nadador.
En este ejemplo, se dan cuatro proposiciones categóricas. Ahora, necesitamos averiguar si las primeras tres proposiciones categóricas deben considerarse como premisas y la cuarta proposición debe considerarse como una conclusión de los sorites o no. Al examinar estas cuatro proposiciones, se encuentra que la primera proposición y la segunda proposición están vinculadas entre sí, pero no están vinculadas entre sí a la tercera proposición. La razón es que, en la tercera proposición, encontramos un nuevo término animales cuadrúpedos que no se encuentra ni en la primera proposición ni en la segunda proposición. Por tanto, la tercera proposición “Ningún animal cuadrúpedo es persona educada” no puede extraerse de la primera y la segunda proposición considerándolas juntas. Además, se observa que la tercera proposición está vinculada a la cuarta proposición (es decir, conclusión). Entonces, falta una proposición en la cadena de silogismos, que necesitamos identificar. Una vez que agreguemos la proposición no declarada a la cadena de silogismos, podremos probar los sorites si es válida o no. Si consideramos las proposiciones primera y segunda, sacaremos la conclusión Todos los nadadores son estudiantes. Pero esta no es la tercera proposición dada en el argumento. Además, esta proposición no está vinculada a la tercera proposición dada, "Ningún animal cuadrúpedo es persona educada". La razón es que no se encuentra un término intermedio entre las proposiciones "Todos los nadadores son estudiantes" y "Ningún animal cuadrúpedo es una persona educada". Por lo tanto, necesitamos agregar una proposición, es decir, "Todos los nadadores son estudiantes" antes de la primera proposición del argumento dado para sacar la conclusión "Todas las personas educadas son nadadores". La conclusión "Todas las personas educadas son nadadores" está vinculada a la proposición "Ningún animal cuadrúpedo es persona educada" y, por lo tanto, ayuda a sacar la conclusión "Ningún animal cuadrúpedo es nadador". Aquí, "Todos los nadadores son estudiantes" se considera como el entimema de primer orden. Los soritos completos se indican a continuación.
Todos los nadadores son estudiantes. (Proposición-1)
Todos los estudiantes son personas educadas. (Proposición-2)
Todas las personas educadas son nadadores. (Proposición-3)
Ningún animal cuadrúpedo es una persona educada. (Proposición-4)
Por lo tanto, ningún animal cuadrúpedo es nadador. (Conclusión)
Este sorites es una cadena de dos silogismos. El primer silogismo consiste en la proposición 1, la proposición 2 y la proposición 3. El segundo silogismo consiste en la proposición 3, la proposición 4 y la conclusión. La proposición categórica "Todas las personas educadas son nadadores" es la conclusión del primer silogismo y la proposición categórica "Ningún animal cuadrúpedo es nadador" es la conclusión del segundo silogismo. Al examinar esta cadena de silogismo, se encuentra que el primer silogismo corresponde a la cuarta figura del silogismo y viola las reglas silogísticas. Se encuentra con una falacia conocida como "menor ilícito". Dado que uno de los constituyentes (primer silogismo) de los sorites no es válido, los sorites se tratan como inválidos.
1.30 Silogismo hipotético puro
En un silogismo hipotético puro, las proposiciones constituyentes deben ser proposiciones hipotéticas. En otras palabras, un silogismo se considera puramente hipotético cuando su premisa mayor, premisa menor y conclusión son proposiciones hipotéticas. Un ejemplo,
Si Migue estudia lógica, aprenderá lecciones. (Premisa mayor)
Si aprende lecciones, obtendrá una buena nota. (Premisa menor)
Si Migue estudia lógica, aprenderá lecciones. (Premisa mayor)
Si aprende lecciones, obtendrá una buena nota. (Premisa menor)
Por lo tanto, si Migue estudia lógica, obtendrá una buena nota. (Conclusión)
En este silogismo, todas las proposiciones constituyentes son proposiciones compuestas porque tienen partes antecedente y consecuente. Las partes antecedente y consecuente se combinan con la expresión "si ... entonces". En la premisa principal, "Migue estudia la lógica" se considera un antecedente, y "Él aprenderá lecciones" se trata como un consecuente. Tanto el antecedente como el consecuente de una proposición hipotética se tratan como proposiciones categóricas. Con esta lógica, podemos afirmar que una proposición hipotética es una proposición compuesta de proposiciones categóricas. El silogismo hipotético puro mencionado anteriormente se puede simbolizar como:
Si X entonces Y. (premisa mayor)
Si Y entonces Z. (premisa menor)
Por lo tanto, si X entonces Z. (Conclusión)
En este silogismo, X, Y y Z se utilizan como variables proposicionales para representar proposiciones categóricas. Un silogismo hipotético puro se considera válido cuando satisface las siguientes condiciones.
(i) Debe haber una proposición categórica común que exista en la premisa mayor y la premisa menor.
(ii) La proposición categórica común será antecedente de una premisa y consecuente de otra premisa.
(iii) La conclusión no debe tener la proposición categórica común, pero debe tener un antecedente de una premisa y un consecuente de otra premisa.
Al aplicar estas tres condiciones a un silogismo hipotético puro, obtenemos dos tipos de silogismo válido. Estos son:
(a) Si X entonces Y.
Si Y entonces Z.
Por lo tanto, si X entonces Z.
(b) Si Y entonces Z.
Si X entonces Y.
Por lo tanto, si X entonces Z.
La violación de cualquiera de estas tres condiciones, el silogismo hipotético puro se consideraría inválido. Por ejemplo,
(a) Si X entonces Y.
Si Y entonces Z.
Por lo tanto, si Z entonces X.
(b) Si Y entonces Z.
Si X entonces Y.
Por lo tanto, si Z entonces X.
(c) Si X entonces Y.
Si Z entonces Y.
Por lo tanto, si X entonces Z.
(d) Si X entonces Y.
Si X entonces Z.
Por lo tanto, si Y entonces Z.
1.31 Silogismo disyuntivo puro
En un silogismo disyuntivo puro, la premisa mayor, la premisa menor y la conclusión son las proposiciones disyuntivas. Una proposición disyuntiva consta de dos proposiciones categóricas combinadas con la expresión “cualquiera ... o". Por ejemplo, "Rogelio es ingeniero o bailarín". En este ejemplo, encontramos dos proposiciones categóricas, "Rogelio es un ingeniero" y "Rogelio es un bailarín", y estas proposiciones se combinan. En el caso de una proposición disyuntiva, ambas proposiciones categóricas son proposiciones afirmativas. Es así porque no podemos formular una proposición disyuntiva negando sus dos alternativas. Además, ni siquiera podemos negar una de sus alternativas de una proposición disyuntiva. Si intentamos negar una de las alternativas a una proposición disyuntiva, cometeremos un error, que se llama estructura incorrecta de la proposición disyuntiva. Por ejemplo, "Ni Nic es cantante ni bailarina". En esta proposición, no podemos afirmar ninguna de sus alternativas, ya que rechaza ambas alternativas. Por tanto, esta proposición no se considera una proposición disyuntiva. Tomemos otro ejemplo, "O Nic es un nadador o no es un bailarín". En esta propuesta, dos alternativas no están vinculadas entre sí. Por tanto, esta proposición tampoco se considera una proposición disyuntiva en el discurso lógico. Dado que una proposición disyuntiva abarca dos proposiciones afirmativas, la regla silogística sobre la calidad no se aplica al silogismo disyuntivo puro. Los silogismos disyuntivos puros rara vez se encuentran en la lógica y el discurso lógico, por lo que los lógicos modernos no le dan mucha importancia al silogismo disyuntivo puro. Para los lógicos modernos, silogismo significa solo silogismo categórico, no cualquier tipo de argumento que tenga meramente dos premisas y una conclusión de muchas variedades. Pero para los lógicos tradicionales, un silogismo debe constar de dos premisas y una conclusión independientemente de la estructura de las proposiciones constituyentes del silogismo. A continuación se muestra un ejemplo de silogismo disyuntivo puro.
Cualquier Ana se casará con Juan o se casará con José. (Premisa mayor)
Cualquier Ana se casará con José o se casará con Miguel. (Premisa menor)
Por lo tanto, Ana se casará con Miguel o se casará con Juan. (Conclusión)
Este silogismo se puede representar simbólicamente como,
Si X entonces Y. (premisa mayor)
Si Y entonces Z. (premisa menor)
Por lo tanto, si X entonces Z. (Conclusión)
Tenga en cuenta que X, Y y Z son las variables proposicionales y representan proposiciones categóricas.
Un silogismo disyuntivo puro se considera válido cuando satisface las siguientes condiciones:
(i) Debe haber una proposición categórica común para la premisa mayor y la premisa menor.
(ii) La proposición categórica común será una de las alternativas a la premisa mayor y la premisa menor.
(iii) La conclusión no debe tener la proposición categórica común, pero debe tener una proposición alternativa de la premisa mayor y la premisa menor.
Al aplicar estas tres condiciones al silogismo disyuntivo puro, obtenemos dos silogismos válidos que se mencionan a continuación simbólicamente.
(a) Cualquier X o Y.
Cualquier Y o Z.
Por lo tanto, Z o X.
(b) Cualquier X o Y.
Cualquier Y o Z.
Por lo tanto, X o Z.
1.32 Silogismo categórico hipotético
Un silogismo categórico hipotético es un silogismo mixto en el que la premisa principal es una proposición hipotética. La premisa menor y la conclusión son las proposiciones categóricas. El antecedente de la premisa mayor es la premisa menor y el consecuente de la premisa mayor es la conclusión del silogismo. Un ejemplo,
Si María viene a la clase de piano, aprenderá las lecciones. (Premisa mayor)
María llega a la clase de piano. (Premisa menor)
Por lo tanto, aprenderá las lecciones. (Conclusión)
Este silogismo se representa simbólicamente como,
Si X entonces Y.
X.
Por tanto, Y.
Tenga en cuenta que el alfabeto X e Y son las variables proposicionales y representan proposiciones categóricas en el argumento mencionado anteriormente. Un silogismo categórico hipotético tiene dos formas válidas: modus ponens y modus tollens. Modus ponens se conoce como silogismo constructivo, mientras que modus tollens se conoce como silogismo negativo. Modus ponens se considera un estado de ánimo afirmativo. La razón es que la palabra ponens se deriva de la palabra latina ponere, que significa "afirmar". Modus ponens tiene las siguientes reglas para validar un argumento.
(i) Afirmar el antecedente de la premisa mayor en la premisa menor, y
(ii) Afirmar el consecuente de la premisa mayor en conclusión.
Al satisfacer estas dos reglas, podemos tener el siguiente modus ponens válido, representado simbólicamente.
(a) Si X entonces Y.
X.
Por tanto, Y.
(b) Si X entonces no Y.
X.
Por lo tanto, no Y.
(c) Si no es X, entonces Y.
Angustia X.
Por tanto, Y.
(d) Si no es X, entonces no Y.
Angustia X.
Por lo tanto, no Y.
Si se da la violación de las reglas del modus ponens, cometemos la falacia conocida como "negar el antecedente". Por ejemplo,
Si X entonces Y. (premisa mayor)
No X. (premisa menor)
Por lo tanto, no Y. (Conclusión)
Este silogismo es falaz porque negamos el antecedente de la premisa mayor en la premisa menor y negamos el consecuente de la premisa mayor en conclusión. Si reducimos este silogismo al silogismo categórico puro, encontramos el siguiente silogismo.
R: Todos los casos de X son casos de Y.
O: Este no es un caso de X.
O: Por lo tanto, este no es un caso de Y.
Este silogismo no es válido porque el término mayor se distribuye en conclusión, pero no se distribuye en la premisa mayor. De ahí que el silogismo cometa una falacia conocida como "ilícita mayor". Modus tollens es también una forma válida de un silogismo categórico hipotético. Se le conoce como silogismo negativo, ya que posee un estado de ánimo negativo. La palabra tollens se deriva de la palabra latina tollere, que significa negar o negar. Modus tollens tiene las siguientes reglas para validar un argumento.
(i) Negar el consecuente de la premisa mayor en la premisa menor, y
(ii) Negar el antecedente de la premisa mayor en conclusión. Una vez cumplidas estas reglas, podemos tener las siguientes tolerancias de modo válidas, como se presenta a continuación simbólicamente.
(a) Si X entonces Y.
No es Y.
Por lo tanto, no X.
(b) Si X entonces no Y.
Y.
Por lo tanto, no X.
(c) Si no es X, entonces Y.
No es Y.
Por tanto, X.
(d) Si no es X, entonces no Y.
Y.
Por tanto, X.
Violación de las reglas del modus tollens, cometemos la falacia conocida como "afirmar el consecuente". Un ejemplo,
Si X entonces Y. (premisa mayor)
Y. (premisa menor)
Por tanto, X. (Conclusión)
Este silogismo es falaz porque afirmamos el consecuente de la premisa mayor en la premisa menor y afirmamos el antecedente de la premisa mayor en conclusión. Si reducimos este silogismo al silogismo categórico puro, encontramos el siguiente silogismo.
A: Todos los casos de X son casos de Y.
I: Este es un caso de Y.
I: Por lo tanto, este es un caso de X.
Este no es un silogismo válido porque el término medio no se distribuye en ninguna de las premisas. Por tanto, el silogismo comete la falacia conocida como "medio no distribuido".
1.33 Silogismo categórico disyuntivo
Un silogismo se trata como silogismo categórico disyuntivo cuando su premisa principal es una proposición disyuntiva. Su premisa menor y la conclusión son proposiciones categóricas. En este silogismo, la premisa menor niega una de las alternativas de las premisas mayores y la conclusión afirma la otra alternativa de la premisa mayor. Dado que no todas las proposiciones constituyentes tienen la misma relación, el silogismo se considera un silogismo mixto. Un ejemplo del silogismo categórico disyuntivo se coloca a continuación.
Cualquier Rogelio es nadador o cantante. (Premisa mayor)
Rogelio no es nadador. (Premisa menor)
Por tanto, Rogelio es cantante. (Conclusión)
Este silogismo se representa simbólicamente como,
Cualquier X o Y. (premisa principal)
No X. (premisa menor)
Por tanto, Y. (Conclusión)
Tenga en cuenta que X e Y se utilizan como variables proposicionales y representan proposiciones categóricas. En este silogismo, con respecto a la premisa mayor, la verdad de una alternativa no implica necesariamente la falsedad de otras alternativas. Más bien, en algunas situaciones, ambas alternativas pueden considerarse verdaderas. Entonces, para averiguar la validez del silogismo, necesitamos aplicarle las reglas del silogismo categórico disyuntivo. La regla dice que negar una de las alternativas de la premisa mayor en la premisa menor es afirmar la otra alternativa de la premisa mayor en conclusión. Los siguientes silogismos válidos satisfacen las reglas del silogismo categórico disyuntivo.
(a) Cualquier X o Y.
Angustia X.
Por tanto, Y.
(b) Cualquier X o Y.
No es Y.
Por tanto, X.
La violación de las reglas del silogismo categórico disyuntivo resultaría en los siguientes silogismos inválidos.
(a) Cualquier X o Y.
X.
Por lo tanto, no Y.
(b) Cualquier X o Y.
Y.
Por lo tanto, no X.
Pero los lógicos modernos afirman que cuando dos proposiciones categóricas alternativas de la premisa mayor son mutuamente excluyentes como proposiciones contradictorias, podemos afirmar una alternativa de la premisa mayor en la premisa menor y negar la otra alternativa de la premisa mayor en conclusión. Al hacer eso, no violaremos las reglas del silogismo categórico disyuntivo. Por ejemplo,
Cualquier Mita es mujer o hombre. (Premisa mayor)
Mita es una mujer. (Premisa menor)
Por tanto, Mita no es un hombre. (Conclusión)
En este silogismo, la verdad de una alternativa implica necesariamente la falsedad de la otra alternativa de la premisa mayor. Por tanto, dos alternativas mencionadas en la premisa principal son mutuamente excluyentes. Pero, cuando dos proposiciones categóricas de una premisa mayor disyuntiva no son mutuamente excluyentes, tenemos que aplicar las reglas del silogismo categórico disyuntivo para comprobar la validez del argumento.
1.34 Dilema
Un dilema es cuando al ser humano le resulta difícil optar por una opción entre dos o muchas alternativas. Por ejemplo, una persona quiere llegar a un destino en diez minutos. En este caso, si espera un autobús del gobierno, es posible que no llegue a su destino a tiempo porque algunos autobuses del gobierno no llegan a tiempo. Si viaja en un auto- compartido, es posible que no llegue a su destino a tiempo porque los auto- compartidos se detienen de vez en cuando y luego reciben más pasajeros en sus rutas. En esta coyuntura, se encuentra en el dilema de optar por un autobús del gobierno o un auto- compartido para llegar al destino. Otro ejemplo, la mayoría de los padres en la India se encuentran en un dilema acerca de si enviar sus recompensas para estudios de ingeniería o medicina que han aprobado el duodécimo examen estándar de ciencias con un alto porcentaje de calificaciones. Un dilema es un silogismo mixto en el que la premisa mayor es una proposición compuesta hipotética, la premisa menor es una proposición disyuntiva y la conclusión es una proposición categórica o disyuntiva. En la premisa menor, necesitamos afirmar el antecedente o negar el consecuente de la premisa mayor. Un ejemplo simbólico de dilema,
Si X entonces Y y si L entonces Y. (premisa principal)
Cualquier X o L. (premisa menor)
Por tanto, Y. (Conclusión)
Aquí, X, Y y L se utilizan como variables proposicionales y representan proposiciones categóricas. El dilema surge en este silogismo debido a su principal premisa hipotética compuesta. La razón está en la premisa menor si queremos afirmar el antecedente, cuyas proposiciones tenemos que tomar en consideración como antecedente de la premisa mayor. ¿Es "Si X entonces Y" o "X y L"? Además, si deseamos negar el consecuente de la premisa mayor en la premisa menor, ¿qué proposiciones deben tomarse en consideración de la premisa mayor? ¿Es "Si L entonces Y" o "Y" solo? El dilema también persiste en la conclusión. Se trata de si la conclusión debe afirmarse o negarse. Si deseamos afirmar las proposiciones en conclusión, entonces, ¿qué proposiciones deben afirmarse, y si deseamos negar las proposiciones en conclusión, entonces, qué proposiciones deben ser negadas? Además, ¿la conclusión debe ser categórica o disyuntiva? Un dilema será juzgado como constructivo o destructivo según la calidad de su premisa menor. En caso de un dilema constructivo, la premisa menor disyuntiva afirma alternativamente el antecedente de la premisa mayor hipotética compuesta. En caso de un dilema destructivo, la premisa menor disyuntiva niega alternativamente el consecuente de la premisa mayor hipotética compuesta. Un dilema que será tratado como simple o complejo se basa en la conclusión del dilema. Si la conclusión es una proposición categórica, el dilema se considera un simple dilema. Pero si la conclusión es una proposición disyuntiva, entonces el dilema se considera un dilema complejo. Considerando un dilema simple, un dilema complejo, dilema constructivo y dilema destructivo, tenemos cuatro formas de dilemas. Estos son,
(i) Dilema constructivo simple
(ii) Dilema constructivo complejo
(iii) Dilema destructivo simple
(iv) Dilema destructivo complejo.
1.35 Formas de dilema
En los siguientes ejemplos de dilemas, X, Y, L y M se utilizan como variables proposicionales y representan proposiciones categóricas.
Dilema constructivo simple
La representación simbólica de un simple dilema constructivo es,
Si X entonces Y y si L entonces Y. (premisa principal)
Cualquier X o L. (premisa menor)
Por tanto, Y. (Conclusión)
Un ejemplo concreto de un simple dilema constructivo es,
Si una mujer se guía por la opinión de los demás, será criticada y si un
la mujer actúa según sus juicios, entonces será criticada.
Una mujer actúa según la opinión de los demás o según su
juicios.
En cualquier caso, será criticada.
La representación simbólica de un dilema constructivo complejo es,
Si X entonces Y y si L entonces M. (premisa mayor)
Cualquier X o L. (premisa menor)
Por lo tanto, o Y o M. (Conclusión)
Un ejemplo concreto de un dilema constructivo complejo es,
Si María canta una canción, será venerada y si Ana juega bádminton, será reconocida.
Cualquier Ana cantará una canción o Maria jugará bádminton. Por lo tanto, se venerará a Ana o se reconocerá a María.
Dilema destructivo simple
La representación simbólica de un simple dilema destructivo es,
Si X entonces Y y si X entonces M. (premisa mayor)
Cualquier no Y o no M. (premisa menor)
Por tanto, no X. (Conclusión)
Un ejemplo concreto de un simple dilema destructivo es,
Si el cielo está despejado, entonces hay sol y si el cielo está despejado, entonces hay luna.
Cualquier no hay sol o no hay luna.
Por tanto, el cielo no está despejado.
Dilema destructivo complejo
La representación simbólica de un complejo dilema destructivo es,
Si X entonces Y y si L entonces M. (premisa mayor)
Cualquier no Y o no M. (premisa menor)
Por lo tanto, o no X o no L. (Conclusión)
Un ejemplo concreto de un dilema destructivo complejo es,
Si un estudiante es obediente, obedecerá las órdenes y si es inteligente, entonces
entenderá las lecciones.
Cualquier no obedece las órdenes o no comprende las lecciones.
Por lo tanto, o no es obediente o no es inteligente.
1.36 Lógica simbólica
1.36.1 Nacimiento de la lógica simbólica
En los manuscritos anteriores, mencionamos que la lógica se ocupa de los argumentos. Los argumentos contienen proposiciones y una proposición consta de unas pocas palabras y de términos. Dado que los argumentos se formulan en lenguaje natural (lenguaje ordinario), las palabras y los términos utilizados en los argumentos a menudo se asocian con vaguedad y ambigüedades y, por lo tanto, confunden (tergiversan/distorsionan) el significado de las proposiciones de los argumentos. Debido al significado engañoso de las proposiciones, la validez e invalidez de un argumento no se determinaría correctamente. Por ejemplo, "Los estudiantes de lógica no son malos". En esta proposición, el término "malo" es vago porque carece de precisión. Puede referirse al comportamiento de los estudiantes de lógica o al desempeño de los estudiantes en los cursos de lógica, o puede referirse además a la capacidad de razonamiento de los estudiantes de lógica. Por lo tanto, para derivar la conclusión del argumento y juzgar la validez y la invalidez del argumento de manera correcta y sencilla, los lógicos propusieron "lógica simbólica" en el sujeto de la lógica. Se observa que los argumentos formulados a través del lenguaje natural son demasiado grandes, ya que consta de unas pocas proposiciones compuestas y complejas. Un argumento involucrado con la complejidad a menudo se enreda con ambigüedades y confusión. Por ejemplo, la diferencia entre el cuadrado de los dos números es igual al producto de la suma y la diferencia de los dos números. Esta expresión está involucrada con la complejidad ya que se formula a través del lenguaje natural. Crea confusión para los lectores a menos que estén al tanto del álgebra elemental, las ecuaciones matemáticas y sus interpretaciones. Pero para evitar confusiones y aportar claridad a esta expresión, se puede traducir a la forma simbólica como x2 - y2 = (x + y) (x - y). En esta expresión simbólica, x e y se consideran variables y se puede asignar cualquier número a estas variables. De esta manera, para detener las lagunas y evitar las deficiencias del lenguaje natural de un argumento, los lógicos intentaron reformar la lógica clásica y desarrollar la "lógica simbólica". En lógica simbólica, cada proposición se comunica a través de una variable proposicional. Entonces, es más fácil averiguar la validez o invalidez de un argumento. Según Mitchell, los símbolos especiales de la lógica simbólica nos permiten exhibir con mayor claridad las estructuras lógicas de los argumentos que pueden quedar oscurecidas por la formulación en lenguaje natural (lenguaje ordinario[64]). Aristóteles introdujo la noción de "variable" al sujeto lógico en el siglo IV. Sus trabajos se limitan a la formulación de la proposición lógica a través de términos sujeto-predicado, descubrir la estructura correcta de la proposición de un argumento, determinar la validez e invalidez de un argumento aplicando las reglas silogísticas, etc. fundamento de la lógica. Por tanto, la lógica aristotélica se denomina lógica clásica. En el siglo XVII, G. W. Von Leibniz (1646-1716) propuso el desarrollo de la lógica clásica. Sugirió que "podría idearse un cálculo universal del razonamiento que proporcionaría un método automático de solución para todos los problemas y que podría expresarse en el lenguaje universal[65]". Siguiendo a Leibniz, George Boole (1815-1864), un matemático-filósofo inglés; Augustus DeMorgan (1806-1871), matemático y lógico nacido en India; Charles Peirce (1839-1914), un filósofo estadounidense, ha elaborado en detalle el tema de la "lógica simbólica" y lo ha mencionado como un tema de estudio independiente. En el siglo XX, el matemático y filósofo alemán Gottlob Frege (1848-1925), el matemático italiano Guiseppe Peano (1858-1935), el matemático y filósofo inglés Alfred North Whitehead (1861-1947), el filósofo británico Bertrand Russell (1872-1970), el filósofo estadounidense CI Lewis (1883-1964), el lógico polaco-estadounidense Alfred Tarski (1901-1983) y algunos otros han contribuido con sus trabajos sobre el tema de la "lógica simbólica[66]". Este tema es ahora rico en su alcance e importante en su aplicación en la formulación de argumentos y su validación. Según Morrill, la lógica simbólica es una rama de la lógica que representa cómo debemos razonar mediante el uso de un lenguaje formal compuesto por símbolos abstractos[67]. En opinión de Whitehead (1911), con la ayuda del simbolismo, podemos hacer transiciones en el razonamiento casi mecánicamente por el ojo, que de otro modo pondrían en juego las facultades superiores del cerebro[68]. Según C. I. Lewis (1883-1964), la lógica simbólica tiene tres componentes esenciales. Estos son ideogramas, variables proposicionales y constantes lógicas (conectivas[69]).
1.36.2 Ideogramas
Los ideogramas son aquellos signos que se utilizan para transmitir ideas o conceptos sobre asuntos mundanos. Estos signos no se transmiten a través de sonidos. Son signos silenciosos. Por ejemplo, signo mayor que >, signo de resta - , etc. El signo mayor que expresa que un valor es mayor que otro valor. El signo de resta indica que menos un número de otro número. Estos signos no tienen ambigüedades ni vaguedades en su uso. Independientemente de la religión, la edad, el género y otras diferencias de los seres humanos, estos signos transmiten el mismo significado a todos. Los ideogramas se utilizan en la lógica simbólica porque transmiten el significado sin ambigüedades. Sus significados no cambian con el tiempo. El uso de ideogramas en lógica simbólica ayuda a determinar el valor de verdad de las proposiciones y la validez de los argumentos. Los fonogramas son aquellos signos que se utilizan para expresar objetos y conceptos de asuntos mundanos a través de sonidos o palabras. En otras palabras, los fonogramas son los sonidos que corresponden a objetos o conceptos del mundo fenoménico. En el lenguaje natural, los fonogramas se transmiten a través de sonidos. Por ejemplo, "signo de interrogación", "resta", "suma", etc., se pronuncian en palabras en el lenguaje natural (es decir, lenguaje ordinario). Dado que el lenguaje natural no está libre de ambigüedades y vaguedades, los fonogramas no son útiles para la lógica simbólica.
1.36.3 Variables proposicionales y conectivas lógicas
En aritmética, los alfabetos ingleses pequeños x, y, z, etc., se utilizan como variables de un enunciado matemático y una ecuación. Estas variables representan un valor o un número. Pero en la lógica simbólica, x, y, z, etc., se utilizan como variables para representar proposiciones. Por tanto, en el discurso de la lógica simbólica, x, y, z, etc., se tratan como variables proposicionales. Por ejemplo, p es una variable proposicional que puede representar "El cielo es azul" o "La hierba es verde" o “Rogelio es un chico alto" o alguna otra proposición. En el caso de una proposición compuesta, se usa más de una variable proposicional para representar la proposición. Digamos, “José es un nadador y Pedro es un jugador de fútbol”. En esta proposición, dos proposiciones se combinan con la palabra "y". Entonces, podemos asignar una variable proposicional única a cada proposición constituyente. Es decir, p significa que Rogelio es un nadador "y q significa que Mario es un jugador de fútbol”. Entonces, podemos escribir "p y q". Una proposición se juzga necesariamente como verdadera o falsa en el discurso lógico. No se puede juzgar como verdadero y falso a la vez. Además, no es posible juzgar una proposición como ni verdadera ni falsa en un momento dado. Por tanto, la verdad y la falsedad de una proposición se consideran valores de la proposición. Si una proposición es verdadera, entonces su negación será falsa, y si una proposición es falsa, entonces su negación se considera verdadera. Entonces, invariablemente, una proposición tiene un valor de verdad. Una variable proposicional representa una variedad de proposiciones en diferentes contextos. Entonces, no tiene ningún significado fijo. Por lo tanto, la mayor consideración de proposicional las variables no bastarían para traducir proposiciones del lenguaje natural en proposiciones simbólicas. Necesitamos constantes lógicas (conectivas) además de variables proposicionales para traducir las proposiciones del lenguaje natural en proposiciones simbólicas. Los conectivos lógicos combinan las variables proposicionales y las ponen juntas en un paréntesis como un todo para transmitir su significado. Los significados de los conectivos lógicos no cambian de vez en cuando, de un argumento a otro argumento, y de un contexto a otro contexto. Sus significados permanecen fijos todo el tiempo. Conectivos lógicos Hay seis conectivos lógicos que se utilizan en lógica simbólica. Además de eso, la "negación" se utiliza como una constante lógica en el discurso lógico. La "negación" se trata como un operador unario porque está destinada a negar una variable proposicional en la lógica simbólica y una proposición en el lenguaje natural. Por lo tanto, no se considera un conectivo lógico sino un operador funcional de verdad. Los seis conectivos lógicos requieren un mínimo de dos variables proposicionales para su conexión y, por lo tanto, se consideran operadores binarios.
Operador unario (constante lógica) ~
Operador binario (conectivos lógicos) ∧, ∨, →, ≡, ↓, |
La constante lógica y las conectivas lógicas son
(i) Negación
(ii) Conjunción
(iii) Disyunción
(iv) Implicación
(v) Equivalencia
(vi) Daga
(vii) Accidente cerebrovascular
La constante lógica y las conectivas lógicas tienen símbolos únicos y distintos
connotaciones. Los detalles se presentan a continuación.
 16.46.33.png)
En lógica simbólica, una variable proposicional representa una proposición simple o atómica. Digamos que "p" es una variable proposicional que representa una proposición atómica (proposición simple) "La nieve es blanca". Escribimos la proposición en forma simbólica como "p". Si se niega la proposición, entonces escribimos "La nieve no es blanca", y su forma simbólica es "~p", que se lee como "no p". Debe notarse aquí que la negación lógica constante 'siempre está asociada con una variable proposicional solamente. Por ejemplo,
p - La nieve es blanca.
~ p - La nieve no es blanca.
~~ p - No es cierto que la nieve no sea blanca.
El símbolo "~" se comunica a través de muchas expresiones de lenguajes naturales, por ejemplo, no es cierto, es falso y no es el caso. Considere un ejemplo; consideremos que p, r, t son variables proposicionales. Estas variables se presentan simbólicamente para las siguientes proposiciones.
~ p - No es cierto que el sol salga por el oeste.
~ r - Es falso que los cuervos sean blancos.
~ t - No es el caso de que las mujeres hermosas sean inmortales.
La conjunción conectiva lógica 'está vinculada a dos proposiciones simples y, por lo tanto, está conectada con dos variables proposicionales a la vez. Se simboliza como "∧" y se lee como "y". Por ejemplo, "m" significa “Rogelio es un buen chico" y "n" significa "Mini es un cantante". Estas dos proposiciones simples se combinan con la conjunción conectiva lógica ", y está escrito como Rogelio es un buen chico y María es un cantante". Esta proposición compuesta se simboliza como "m ∧ n". A continuación se mencionan algunos ejemplos más.
m - Rogelio es un buen chico.
n - María es cantante.
m ∧ n - Rogelio es un buen chico y María es cantante.
~ m ∧ n - Rogelio no es un buen chico y María es cantante.
m ∧ ~ n - Rogelio es un buen chico y María no es cantante.
~ m ∧ ~ n - Rogelio no es un buen chico y María no es cantante.
El símbolo lógico “∧” se puede usar para las siguientes expresiones del lenguaje natural, pero no se limita solo a estas, ambos, aunque, pero, sin embargo, además, todavía, etc. Tome un ejemplo, considere p, r, n, m son las variables proposicionales. Estas variables se presentan simbólicamente para las siguientes proposiciones.
p - María es nadadora.
r - María es una chica bajita.
n - María es sincera.
m - Gita es nadadora.
p ∧ r - María es nadadora pero es una niña pequeña.
p ∧ ~ n - María es nadadora aunque no es sincera.
m p - Tanto Gita como María son nadadores.
~ n ∧ p - María no es sincera, pero es nadadora.
La "disyunción" conectiva lógica está vinculada a dos variables proposicionales y, por lo tanto, está asociada a una proposición compuesta. Está simbolizado como "∨". Por ejemplo, x significa "La nieve es blanca" e y significa "La hierba es verde". Si estas dos proposiciones simples se combinan con la disyunción conectiva lógica, se convertiría en una proposición compuesta. Esta proposición compuesta se escribe como "O la nieve es blanca o la hierba es verde". Se presenta simbólicamente como "x" ∨ y". A continuación se mencionan algunos ejemplos.
x - La nieve es blanca.
y - La hierba es verde.
x ∨ y: la nieve es blanca o la hierba es verde.
~ x ∨ y: la nieve no es blanca o la hierba es verde.
x ∨ ~ y: la nieve es blanca o la hierba no es verde.
~ x ∨ ~ y: la nieve no es blanca o la hierba no es verde.
Una proposición lógica formulada con una expresión "si-entonces" se llama proposición hipotética o implicativa o condicional. La proposición hipotética consta de dos partes, a saber, antecedente y consecuente. La implicación conectiva lógica se conecta con dos partes (es decir, dos variables proposicionales) y establece su relación. "Implicación" se simboliza como "→". Tome un ejemplo, considere dos proposiciones simples; “Ana vendrá al patio de recreo" y “Rogelio devolverá sus notas de clase". Si combinamos estas dos proposiciones con el conectivo lógico "implicación", la proposición compuesta se escribiría como "Si Rogelio vendrá al patio de recreo, José devolverá sus apuntes de clase". Esta proposición hipotética se simboliza como "x → y". Algunos ejemplos más son los siguientes:
x - María vendrá al patio de recreo.
y - Ana devolverá sus notas de clase.
x → y - Si María va al patio de recreo, Ana devolverá sus notas de clase.
~ x → y - Si María no viene al patio de recreo, Ana devolverá sus notas de clase.
x → ~ y - Si María va al patio de recreo, Ana no devolverá sus notas de clase.
~ x → ~ y - Si Ana no viene al patio de recreo, Ana no devolverá sus notas de clase.
La "equivalencia" conectiva lógica se conoce popularmente como "bicondicional". Se relaciona con dos proposiciones atómicas o simples que se combinan con una expresión sí y sólo si ". La expresión si y solo si "se simboliza como" ≡ ". Por ejemplo, "p" significa "Serás ascendido en el trabajo" y "q" significa "Calificarás en el examen escrito". Si estas dos proposiciones simples se combinaran con el conectivo lógico "equivalencia", entonces se convertiría en una proposición compuesta y sería estar escrito como "Serás ascendido en el puesto si y solo si calificas para el examen escrito". Esta proposición compuesta se representa simbólicamente como "x ≡ y". A continuación se ofrecen algunos ejemplos más.
p - Serás ascendido en el puesto.
q - Calificarás la prueba escrita.
p ≡ q - Serás ascendido en el trabajo si y solo si calificas para el examen escrito.
~ p ≡ q - No serás promovido en el trabajo si y solo si calificas para el examen escrito.
p ≡ ~ q - Serás ascendido en el trabajo si y solo si no calificas para el examen escrito.
~ p ≡ ~ q - No serás promovido en el trabajo si y solo si no calificas la prueba escrita.
La "daga" conectiva lógica se simboliza como "↓". Connota "ninguno no”. Se entiende como "negación conjunta". Se conecta con dos variables proposicionales simples. Por ejemplo, "p" significa "Él es honesto" y "q" significa "Es estudioso". Si estas dos simples proposiciones se combinan con el conectivo lógico "daga", entonces se escribiría como "Ni él es honesto ni es estudioso". Esta proposición compuesta se simboliza como "p ↓ q". A continuación se colocan algunos ejemplos relacionados con el conector daga.
p - Es honesto.
q - Es estudioso.
p ↓ q - Ni es honrado ni estudioso.
~ p ↓ q - Ni no es honesto ni es estudioso.
p ↓ ~ q - Ni es honrado ni estudioso.
~ p ↓ ~ q - Ni no es honesto ni estudioso.
El "trazo" es un conectivo lógico y un operador binario. Se conecta con dos proposiciones simples y formula una proposición compuesta. Está simbolizado como "|". Se expresa sobre la "negación alternativa" de la proposición compuesta. No connota ambos ”. Por ejemplo, "b" significa "Es una silla" y "q" significa "Es una mesa". Si estas dos proposiciones simples se combinaran con el trazo conectivo lógico", entonces se convertiría en una proposición compuesta y se escribiría como No es tanto una silla como una mesa". Se simboliza como "p | q ’.
p - Es una silla.
q - Es una mesa.
p | q - No es una silla y una mesa a la vez.
Un argumento simbólico consta de algunas proposiciones simbólicas. Cada proposición simbólica consta de unas pocas variables proposicionales y constantes lógicas, así como conectivos lógicos. Si una proposición simbólica compuesta consta de muchas variables proposicionales y conectivos lógicos junto con constantes lógicas, entonces tenemos que limitar el alcance de cada proposición que está unida con otra proposición. Para hacerlo, necesitamos usar paréntesis "()", llaves "{}" y corchetes "[]" en un orden jerárquico en la proposición. Esto nos ayudaría a mantener en orden las proposiciones simbólicas y aclarar el vínculo entre dos proposiciones simbólicas en un argumento.
 12.46.30.png)
Las proposiciones simbólicas se formulan con variables proposicionales, constantes lógicas, conectivos lógicos con paréntesis, llaves y corchetes apropiados cuando sea necesario. Si una proposición compuesta simbólica consta de más de dos variables y conectivos lógicos, entonces necesitamos identificar el conectivo lógico principal de la proposición. El conectivo lógico principal ayuda a identificar la relación entre dos proposiciones. El conectivo lógico principal también guía en la traducción de proposiciones simbólicas a la proposición lógica del lenguaje natural. Al identificar los paréntesis, llaves y corchetes correctos de una proposición simbólica, podemos identificar su conectivo lógico principal. Los paréntesis, llaves y corchetes limitan el alcance de las proposiciones compuestas de la proposición simbólica. La técnica para identificar la conexión lógica principal de una proposición simbólica se aclara a continuación. Consideremos la proposición simbólica [{~ (p ∧ s) → (q ∨ r)} ∨ p]. En esta propuesta, el más a la derecha "tiene el mayor alcance. Se trata como el conectivo lógico principal de la proposición porque contiene otros conectivos lógicos y constantes lógicas en su alcance. El tema conectivo lógico "∨" se conecta con dos proposiciones "{~ (p ∧ s) → (q ∨ r)}" y "p". A continuación, la conectiva lógica principal de la proposición "{~ (p ∧ s) → (q ∨ r)}" es "→". Es así porque "~ (p ∧ s)" y "(q ∨ r)" están en su alcance. A continuación, en consideración de la proposición "(q ∨ r)", la conectiva lógica principal es "∨", ya que conecta las proposiciones "q" y "r". En consideración de la proposición '~ (p s)', es el '~' lo que niega la proposición compuesta 'p' s. Es el alcance mínimo de la proposición compuesta. Además, es el "∧" el que representa la conexión lógica principal de "p" y "s". Identificar el conectivo lógico principal de algunas de las proposiciones simbólicas.
Proposición simbólica Constante lógica principal o conectiva
 12.34.03.png)
Ahora, vamos a formular argumentos simbólicos a partir de proposiciones simbólicas.
Consideremos las siguientes proposiciones simbólicas.
(i) {((p → q) ∧ p) → q}
(ii) {((p → q) ∧ ~ q) → ~ p}
(iii) {((p → q) ∧ ~ p) → ~ q}
(iv) {(~ (p ∧ q) ∧ p) → ~ q}
(v) {((p ∨ q) ∧ ~ p) → q}
(vi) [{(p ∧ ~ r) ∧ (~ r ∨ q)} → ((r ∨ q) ∧ ~ p)]
Considere la proposición simbólica {((p → q) ∧ p) → q}. En esta proposición, la conexión lógica principal es "→". La principal implicación conectiva lógica "se conecta con el antecedente ((p → q) ∧ p) y la consecuente q de la proposición. En el consecuente, se encuentra una variable proposicional (proposición simple) q. Este consecuente se deriva del antecedente ((p → q) ∧ p). Con respecto al antecedente de la proposición, "∧" es el conectivo lógico principal del antecedente según el paréntesis. Por lo tanto, el antecedente consta de dos proposiciones, una proposición compuesta (p → q) y una proposición simple p. La proposición compuesta y la proposición simple juntas concluyen q, como consecuencia de la proposición. Por lo tanto, podemos decir que q "se sigue del antecedente ((p → q) ∧ p). Mientras que la proposición simbólica se traduce a una forma de argumento, tenemos que identificar el conectivo lógico principal de la proposición simbólica. La conexión lógica principal de la proposición simbólica es principalmente "→". Representa la expresión "si entonces". La parte consecuente de la proposición simbólica se considera una conclusión, y la parte o partes precedentes se consideran premisas del argumento.
En un argumento, escribimos las premisas en forma de proposiciones y sacamos una conclusión a partir de las premisas considerándolas juntas. Un argumento simbólico se puede formular a partir de la proposición simbólica {((p → q) ∧ p) → q} de la siguiente manera.
(i) Proposición simbólica: {((p → q) ∧ p) → q}
Argumento simbólico
Premisa 1: (p → q)
Premisa 2: p
Conclusión: Por tanto, q.
(ii) Proposición simbólica: {((p → q) ∧ ~ q) → ~ p}
Argumento simbólico
Premisa 1: (p → q)
Premisa 2: ~ q
Conclusión: Por lo tanto, ~ p.
(iii) Proposición simbólica: {((p → q) ∧ ~ p) → ~ q}
Argumento simbólico
Premisa 1: (p → q)
Premisa 2: ~ p
Conclusión: Por lo tanto, ~ q.
(iv) Proposición simbólica: {(~ (p ∧ q) ∧ p) → ~ q}
Argumento simbólico
Premisa 1: ~ (p ∧ q)
Premisa 2: p
Conclusión: Por lo tanto, ~ q
(v) Proposición simbólica: {((p ∨ q) ∧ ~ p) → q}
Argumento simbólico
Premisa 1: (p ∨ q)
Premisa 2: ~ p
Conclusión: Por lo tanto, q
(vi) Proposición simbólica: [{(p ∧ ~ r) ∧ (~ r ∨ q)} → ((r ∨ q) ∧ ~ p)]
Argumento simbólico
Premisa 1: (p ∧ ~ r)
Premisa 2: (~ r ∨ q)
Conclusión: Por lo tanto, (r ∨ q) ∧ ~ p
También podemos convertir un argumento simbólico en una proposición simbólica. En otras palabras, podemos formular una proposición simbólica considerando las premisas y la conclusión de un argumento simbólico. Consideremos el siguiente argumento simbólico.
Argumento simbólico
Premisa 1: (p ∨ q)
Premisa 2: p
Conclusión: Por tanto q.
Este argumento consta de dos premisas y una conclusión. Dos premisas juntas ayudan a sacar la conclusión. Se requiere que las premisas estén unidas por "∧" al convertirlas en una proposición simbólica. Las premisas se consideran un antecedente de la proposición simbólica porque concluyen el argumento juntas. La conclusión del argumento se trata como una consecuencia de la proposición simbólica. Dado que un argumento consta de premisas y una conclusión, y la conclusión se deriva de las premisas, todo el argumento se simboliza como forma "si-entonces". Así, "si-entonces" sería la conexión lógica principal de la proposición simbólica. El conectivo lógico "si-entonces" se simboliza como "→". Por tanto, podemos formular la siguiente proposición simbólica a partir de este argumento.
Proposición simbólica: {((p ∨ q) ∧ p) → q}.
A continuación se mencionan algunos ejemplos más, que convierten argumentos simbólicos en proposiciones simbólicas.
Premisa 1: (p → q)
Premisa 2: ~ q
Conclusión: Por lo tanto, ~ p
La proposición simbólica de este argumento: {((p → q) ∧ ~ q) → ~ p}
Premisa 1: (p ∧ ~ q)
Premisa 2: (p → q)
Premisa 3: (~ q ∨ ~ p)
Conclusión: Por lo tanto, (~ q → p)
La proposición simbólica de este argumento: [{(p ∧ ~ q) ∧ (p → q) ∧ (~ q ∨ ~ p)}
→ (~ q → p)]
Premisa 1: ~ (p ∧ q)
Premisa 2: p
Conclusión: Por lo tanto, ~ q
La proposición simbólica de este argumento: {(~ (p ∧ q) ∧ p) → ~ q}
Premisa 1: (~ p → q)
Premisa 2: (q → r)
Premisa 3: (~ r → s)
Conclusión: Por lo tanto, ~ (~ p → s)
La proposición simbólica de este argumento: [{((~ p → q) ∧ (q → r)) ∧ (~ r → s)}
→ ~ (~ p → s)]
Premisa 1: (p → (~ q → r))
Premisa 2: (p ∧ ~ r)
Premisa 3: q
Conclusión: Por lo tanto, (~ q ∧ p)
La proposición simbólica de este argumento: [{((p → (~ q → r)) ∧ (p ∧ ~ r)) ∧ q}
→ (~ q ∧ p)]
Premisa 1: ~ p
Premisa 2: (q ∨ r)
Premisa 3: ~ r
Conclusión: Por lo tanto, (~ p ∧ r)
La proposición simbólica de este argumento: [{(~ p ∧ (q ∨ r)) ∧ ~ r} → (~ p ∧ r)]
Hay casos en los que las proposiciones simbólicas constan de más de tres variables proposicionales, algunas conectivas lógicas y, además, muchos paréntesis, llaves y corchetes. Debido al uso frecuente y repetitivo de paréntesis, llaves y corchetes en una proposición simbólica, no sería fácil discernir cada proposición compleja y compuesta dentro de la proposición simbólica y descubrir la conexión lógica principal de cada proposición compuesta y compleja. Para detener estos inconvenientes y hacer que las proposiciones simbólicas sean más fáciles de usar, J. Lukasiewicz (1878-1956), un lógico polaco, desarrolló cuatro notaciones lógicas (N, A, K, C) que corresponden a símbolos lógicos ~, ∨, ∧ , →, respectivamente[70]. Las notaciones lógicas deben escribirse en mayúsculas en inglés y las variables proposicionales deben estar en minúsculas, como p, q, r, s, para una proposición simbólica. Las variables proposicionales deben escribirse inmediatamente después de las notaciones lógicas de una proposición simbólica. En el caso de una proposición simbólica compuesta, donde hay dos variables proposicionales y que están conectadas con un conectivo lógico, estas dos variables deben escribirse cronológicamente junto a la notación lógica del símbolo lógico. Por ejemplo,
Símbolos lógicos Notación lógica Proposición simbólica Notación simbólico
 12.51.24.png)
Al adoptar notaciones lógicas, podemos formular proposiciones simbólicas compuestas y complejas fácilmente y evitar el inconveniente de poner muchos paréntesis, llaves y corchetes en la proposición simbólica. Los siguientes ejemplos muestran cómo traducir proposiciones simbólicas a proposiciones de notación simbólica a través de notaciones lógicas.
(i) p ∧ (p ∧ q)
(ii) p ∧ ~ q
(iii) (p → ~ q) ∧ r
(iv) (~ p ∨ r) ∨ (q ∧ p)
(v) ~ p ∧ (~ q ∧ ~ r)
(vi) ~ (p ∧ ~ q) → (~ q → ~ r)
Consideremos la proposición simbólica "p" (p ∧ q) ". En esta proposición, encontramos dos variables proposicionales p 'y' q 'y una conectiva lógica' ∧ '. La conectiva lógica principal de la proposición simbólica es "∧", ya que se conecta con "p" y "(p ∧ q)". Además, la proposición compuesta "(p ∧ q)" tiene dos variables "p" y "q" y un conectivo lógico "∧". De acuerdo con las pautas de notación lógica, podemos traducir "(p ∧ q)" como Kpq, y luego, "p" (p ∧ q) "traducido como KpKpq. La notación lógica principal de una proposición simbólica debe escribirse al comienzo de la proposición simbólica.
Proposición simbólica: p ∧ (p ∧ q)
Paso 1: p ∧ Kpq
Paso 2: KpKpq
La proposición simbólica 'p' (p 'q)' se traduce como KpKpq.
Proposición simbólica: p ∧ ~ q
Paso 1: p ∧ Nq
Paso 2: KpNq
La proposición simbólica "(p ∧ ~ q)" se traduce como KpNq.
Proposición simbólica: (p → ~ q) ∧ r
Paso 1: (p → Nq) ∧ r
Paso 2: CpNq ∧ r
Paso 3: KCpNqr
La proposición simbólica "(p → ~ q) ∧ r" se traduce como KCpNqr.
Proposición simbólica: (~ p ∨ r) ∨ (q ∧ p)
Paso 1: (Np ∨ r) ∨ (q ∧ p)
Paso 2: (ANpr) ∨ (q ∧ p)
Paso 3: (ANpr) ∨ (Kqp)
Paso 4: AANprKqp
La proposición simbólica "(~ p ∨ r) ∨ (q ∧ p)" se traduce como AANprKqp.
Proposición simbólica: ~ p ∧ (~ q ∧ ~ r)
Paso 1: Np ∧ (Nq ∧ Nr)
Paso 2: Np ∧ KNqNr
Paso 3: KNpKNqNr
La proposición simbólica "~ p ∧ (~ q ∧ ~ r)" se traduce como KNpKNqNr.
Proposición simbólica: ~ (p ∧ ~ q) → (~ q → ~ r)
Paso 1: ~ (p ∧ Nq) → (Nq → Nr)
Paso 2: ~ (KpNq) → (CNqNr)
Paso 3: (NKpNq) → (CNqNr)
Paso 4: CNKpNqCNqNr
La proposición simbólica '~ (p ∧ ~ q) → (~ q → ~ r)' se traduce como CNKpNqCNqNr.
Ahora, podemos traducir proposiciones de notación simbólica en proposiciones simbólicas adoptando las pautas de notación lógica.
(i) CqKqp
(ii) ACprr
(iii) CCNqNpCpq
(iv) NANpq
(v) ANPANrq
(vi) ANpAqNr
(vii) NAANpqr
(viii) CNApKqpACNrqp.
Consideremos la proposición de notación simbólica "CqKqp". Esta proposición tiene dos variables proposicionales “p” y “q” y dos conectivos lógicos C y K. La notación lógica C se consideraría como el conectivo lógico principal de la proposición simbólica, ya que se coloca al comienzo de la proposición de notación simbólica. Dado que la notación lógica C representa el símbolo lógico "→", se conecta con dos variables proposicionales, "q" y "Kqp". Además, Kqp se traduce como “q” “p”. Por lo tanto, "CqKqp" se traduce como "(q → (q ∧ p))".
Proposición de notación simbólica: CqKqp
Paso 1: Cq (q ∧ p)
Paso 2: (q → (q ∧ p))
Por tanto, CqKqp se traduce como (q → (q ∧ p)).
Proposición de notación simbólica: ACprr
Paso 1: A (p → r) r
Paso 2: ((p → r) ∨ r)
Por lo tanto, ACprr se traduce como ((p → r) ∨ r).
Proposición de notación simbólica: CCNqNpCpq
Paso 1: CC ~ q ~ pCpq
Paso 2: C (~ q → ~ p) Cpq
Paso 3: C (~ q → ~ p) (p → q)
Paso 4: ((~ q → ~ p) → (p → q))
Por lo tanto, CCNqNpCpq se traduce como ((~ q → ~ p) → (p → q)).
Proposición de notación simbólica: NANpq
Paso 1: NA ~ pq
Paso 2: N (~ p ∨ q)
Paso 3: ~ (~ p ∨ q)
Por tanto, NANpq se traduce como ~ (~ p ∨ q).
Proposición de notación simbólica: ANpANrq
Paso 1: A ~ pA ~ rq
Paso 2: A ~ p (~ r ∨ q)
Paso 3: (~ p ∨ (~ r ∨ q))
Por lo tanto, ANpANrq se traduce como (~ p ∨ (~ r ∨ q)).
Proposición de notación simbólica: ANpAqNr
Paso 1: A ~ pAq ~ r
Paso 2: A ~ p (q ∨ ~ r)
Paso 3: (~ p ∨ (q ∨ ~ r))
Por lo tanto, ANpAqNr se traduce como (~ p ∨ (q ∨ ~ r)).
Proposición de notación simbólica: NAANpqr
Paso 1: NAA ~ pqr
Paso 2: NA (~ p ∨ q) r
Paso 3: N ((~ p ∨ q) ∨ r)
Paso 4: ~ ((~ p ∨ q) ∨ r)
Por lo tanto, NAANpqr se traduce como ~ ((~ p ∨ q) ∨ r).
Proposición de notación simbólica: CNApKqpACNrqp
Paso 1: CNApKqpAC ~ rqp
Paso 2: CNAp (q ∧ p) A (~ r → q) p
Paso 3: CN (p ∨ (q ∧ p)) A (~ r → q) p
Paso 4: C {~ (p ∨ (q ∧ p))} A (~ r → q) p
Paso 5: C {~ (p ∨ (q ∧ p))} ((~ r → q) ∨ p)
Paso 6: [{~ (p ∨ (q ∧ p))} → ((~ r → q) ∨ p)]
Por lo tanto, CNApKqpACNrqp se traduce como [{~ (p ∨ (q ∧ p))} → ((~ r → q) ∨ p)].
1.36.4 Traducción de proposiciones lógicas en simbólicas
En nuestra vida mundana, utilizamos muchas proposiciones lógicas para transmitir nuestros pensamientos. Por ejemplo, el cielo es azul, la hierba es verde, la nieve es blanca, los estudiantes de lógica son seres sabios, etc. Surge una pregunta, ¿podemos traducir estas proposiciones lógicas en proposiciones simbólicas? Si podemos hacerlo, nos resultaría más fácil utilizar las proposiciones simbólicas en la formulación de argumentos y descubrir la validez o invalidez de los argumentos de forma fácil e inteligible. En esta sección, traduciremos las proposiciones lógicas en proposiciones simbólicas. Luego, traduzca las proposiciones simbólicas en proposiciones lógicas. A partir de entonces, traduciremos los argumentos lógicos en argumentos simbólicos y viceversa. Dejemos que "p" represente la proposición "Él es alto" y "q" represente la proposición "Él es guapo". Considerando las dos variables proposicionales para las proposiciones lógicas, traduzcamos las siguientes proposiciones proposicionales a proposiciones simbólicas.
(i) Es alto pero no guapo.
(ii) Es una persona alta y guapa.
(iii) Es falso que sea bajo y guapo.
(iv) Es alto o guapo.
(v) Es una persona guapa pero no alta.
(vi) No es cierto que sea bajo o no guapo.
(vii) Dado que es alto, debe ser guapo.
Al traducir estas proposiciones lógicas a proposiciones simbólicas, ¿quién no debe cambiar la semántica de las proposiciones? Si lo hacemos, entonces toda la simbolización saldrá mal, ya que la constante lógica y las conectivas lógicas cambiarán debido al cambio de significado de las proposiciones. Por tanto, el significado de las proposiciones lógicas y su traducción de proposiciones simbólicas permanecerán inalteradas en caso de una traducción correcta. La traducción de las proposiciones antes mencionadas a las proposiciones simbólicas se menciona a continuación en orden secuencial.
(i) p ∧ ~q
(ii) q ∧ p
(iii) ~(~p ∧ q)
(iv) p ∨ q
(v) q ∧ ~p
(vi) ~(~p ∨ ~q)
(vii) p→q
Ahora, traduciremos las proposiciones simbólicas en proposiciones lógicas. Dejemos que "p" represente la proposición "Es una noche de luna llena" y "q" represente la proposición "Te ves hermosa". Considerando estas variables proposicionales, estamos traduciendo las siguientes proposiciones simbólicas en proposiciones lógicas.
(i) p ∧ q
(ii) ~ q ∧ ~ p
(iii) ~ (~ p ∨ q)
(iv) ~~ p
(v) ((p ∧ ~ q) → q)
(vi) {~ (p ∧ (~ p ∨ q)) ∨ ~ q}
Al traducir estas proposiciones simbólicas a proposiciones lógicas del lenguaje natural, no podemos permitirnos perder ninguna constante lógica y conectivo lógico de la proposición simbólica. Además, debemos prestar la máxima atención a los paréntesis, llaves y corchetes de la proposición simbólica al traducir una proposición compuesta y compleja a una proposición lógica. La traducción no cambiará el significado de la proposición simbólica. Si cambia, se alterará el significado de las proposiciones lógicas. La semántica de las proposiciones simbólicas y su traducción de proposiciones lógicas deben permanecer sin cambios. La traducción de las proposiciones simbólicas antes mencionadas a proposiciones lógicas se menciona a continuación de forma secuencial.
(i) Es noche de luna y te ves hermosa.
(ii) No te ves hermosa y no es una noche de luna.
(iii) Es falso que o no es una noche de luna llena o te ves hermosa.
(iv) Es falso que no sea una noche de luna.
(v) Si es una noche de luna y no te ves hermosa, entonces te ves hermosa.
(vi) Cualquier es falso, es una noche iluminada por la luna, y o no es una noche iluminada por la luna, o te ves hermosa, o no te ves hermosa.
Ahora, traduciremos los siguientes argumentos lógicos en argumentos simbólicos asignando una variable proposicional a cada oración del argumento. Una oración termina con un punto, puede ser una oración simple o una oración compuesta. Los términos por lo tanto "," así "," por lo tanto ", etc., están asociados con la conclusión del argumento.
(a) Si veo un partido de cricket en la televisión, entonces no puedo estudiar para el examen de fin de semestre. Si no estudio para el examen de fin de semestre, mañana o no apareceré en el examen de fin de semestre o me presentaré al examen de recuperación. Apareceré mañana en el examen de fin de semestre. Por lo tanto, estudiaré para el examen de fin de semestre.
Argumento simbólico:
Veré un partido de cricket en la televisión - p
Estudio para el examen de fin de semestre - q
Apareceré en el examen de fin de semestre - r
Me sentaré para el examen de recuperación - s
Primera premisa: (p → ~ q)
2da premisa: (~ q → (~ r ∨ s))
3ra premisa: r
Conclusión: q
(b) Si la lógica le resulta difícil, debe asistir a todas las clases. Debes estudiar lecciones en tu casa. No estudias lecciones en tu casa y no asistes a las clases. Por tanto, la lógica te resulta difícil.
Argumento simbólico:
La lógica es difícil para ti - p
Tienes que asistir a todas las clases - q
Debes estudiar lecciones en tu casa - r
1ra premisa: p → q
2da premisa: r
Tercera premisa: ~ r ∧ ~ q
Conclusión: p
(c) Rogelio obtendrá el trabajo solo si Juan no aparece en la entrevista de trabajo.
Mario apareció en la entrevista de trabajo. Por lo tanto, María no consiguió el trabajo.
Argumento simbólico:
Maria conseguirá el trabajo - p
Rogelio aparece en la entrevista de trabajo - q
Primera premisa: ~ q → p
2da premisa: q
Conclusión: ~ p
(d) Una enfermedad es contagiosa o hereditaria. La malaria es una enfermedad contagiosa.
Por tanto, no es hereditario.
Argumento simbólico:
Una enfermedad es contagiosa - p
Una enfermedad es hereditaria - q
La malaria es una enfermedad contagiosa - r
La malaria es hereditaria - s
Primera premisa: p ∨ q
2da premisa: r
Conclusión: ~ s.
(e) Si un estudiante está interesado en los estudios, entonces disfrutará de los estudios y prestará atención a las lecciones. Si un estudiante no presta atención a las lecciones, entonces no aprenderá las lecciones. Si no aprende las lecciones, entonces no está disfrutando de los estudios o no está prestando atención a las lecciones. Ella no aprende las lecciones. Por tanto, no le interesan los estudios.
Argumento simbólico:
Un estudiante está interesado en estudios - p
Ella disfrutará de los estudios - q
Ella prestará atención a las lecciones - r
Ella aprenderá las lecciones - s
Ella puede hacerlo bien en el examen - t
Primera premisa: p → (q ∧ r)
2da premisa: ~ r → ~ s
Tercera premisa: ~ s → (~ q ∨ ~ r)
Cuarta premisa: ~ s
Conclusión: ~ p
Ahora traduciremos argumentos simbólicos en argumentos lógicos. Al traducir los argumentos simbólicos, necesitamos descubrir la conexión lógica principal de las premisas compuestas del argumento. Además, debemos notar las variables proposicionales utilizadas en el argumento. Además de estas tareas, debemos considerar que la "conclusión" del argumento simbólico es el consecuente y las premisas son un antecedente del argumento lógico. La conclusión del argumento simbólico se escribirá mencionando "por lo tanto", "por lo tanto", "así", etc., en la oración lógica. Por ejemplo,
Ejemplo 1
Sea "p" para "hay sol" y "q" para "hay luz".
1ra premisa: p → q
2da premisa: p
Conclusión: q
Argumento lógico:
Si hay sol, hay luz. Hay sol. Por tanto, hay luz.
Ejemplo 2
Sea "p" para "hay sol" y "q" para "hay luz".
1ra premisa: p → q
2da premisa: ~ q
Conclusión: ~ p
Argumento lógico:
Si hay sol, hay luz. No hay luz. Por tanto, no hay sol.
Ejemplo-3
Sea p - Un maestro sabía que el límite de velocidad es de treinta kilómetros por hora.
q - Habría estado conduciendo a los setenta.
r - Fue capturada por la policía de tránsito.
Primera premisa: p → ~ q
2da premisa: ~ p ∧ r
Conclusión: ~ p ∨ r
Argumento lógico: si una maestra supiera que el límite de velocidad es de treinta kilómetros por hora, entonces no habría estado conduciendo a setenta. El profesor no sabía que el límite de velocidad es de treinta kilómetros por hora. Conducía a setenta kilómetros por hora y fue detenida por la policía de tránsito. Así, o la profesora no sabía que el límite de velocidad es de treinta kilómetros por hora, o fue capturada por la policía de tránsito. Como se explicó anteriormente, podemos traducir proposiciones lógicas en proposiciones simbólicas y proposiciones simbólicas en proposiciones lógicas. También podemos traducir argumentos lógicos en argumentos simbólicos y argumentos simbólicos en argumentos lógicos. Además, podemos traducir argumentos simbólicos en proposiciones simbólicas. Los lógicos también están interesados en determinar el valor de verdad de una proposición y la validez e invalidez de un argumento. Debido a este interés, buscan las funciones de verdad de una proposición.
1.36.5 Funciones de verdad y método de tabla de verdad
Una proposición lógica no puede ser ni verdadera ni falsa. No puede ser verdadero y falso al mismo tiempo. Más bien, es "verdadero" o "falso". Entonces, la verdad y la falsedad son los dos valores de una proposición lógica. Estos dos valores se conocen como "valores de verdad" de una proposición. En lógica simbólica, una proposición está vinculada a otra proposición con un conectivo lógico. Dado que cada conectivo lógico es único debido a su semántica y sus funciones, el valor de verdad de una proposición compuesta daría como resultado valores de verdad únicos.
Es conveniente para nosotros escribir la letra T mayúscula para la verdad y la letra F mayúscula para la falsedad de una proposición. Si una proposición es T, entonces su negación es F, y si una proposición es F, entonces su negación es T. Por lo tanto, la función de verdad de una proposición negativa se basa en el valor de verdad de la proposición. Por ejemplo, si "La hierba es verde" es verdadera, entonces "La hierba no es verde" es falsa. Nuevamente, si "La hierba es verde" es falsa, entonces "La hierba no es verde" es verdadera. Cuando las funciones de verdad se presentan en una tabla, se denomina "tabla de verdad".
Función de verdad de la negación P
 16.21.50.png)
La negación de una proposición es la función de verdad de esa proposición. Independientemente de la proposición simple o la proposición compuesta, la negación de una proposición es contradictoria con esa proposición. Una variable proposicional tiene dos valores de verdad, T y F. Los valores de verdad de la negación de una proposición se ilustran mediante el método de la tabla de verdad en lo anterior. Aquí, la tabla de verdad consta de dos filas y dos columnas como se muestra arriba. Las dos filas son exhaustivas para mencionar la posible combinación de los valores de verdad de una variable proposicional. Cabe señalar aquí que si hay dos negaciones para una variable proposicional, entonces el valor de verdad de la doble negación de esa proposición sigue siendo el mismo que el valor de verdad de la proposición. Por ejemplo, si p es verdadero, entonces ~~ p es verdadero, y si p es falso, entonces ~~ p es falso.
 16.21.56.png)
Al considerar dos variables proposicionales que se conectan con una conectiva lógica, podemos tener combinaciones de cuatro posibles valores de verdad. Estos son TT, TF, FT y FF. Estos valores de verdad se organizan en un orden teniendo en cuenta la distribución equitativa y adecuada de los valores de verdad y falso entre dos variables proposicionales. Si p y q son dos variables proposicionales que se conectan con una conectiva lógica, digamos "→", entonces p tendría valores TTFF, y q tendría valores TFTF para determinar la función de verdad de p → q. A continuación se dibuja una tabla de verdad con fines ilustrativos sin mencionar la función de verdad de p → q, que se explicaría un poco más adelante en este capítulo.
 16.24.29.png)
En el caso de tres variables proposicionales de una proposición simbólica, digamos, '((p ∧ q) ∧ r)', puede tener una combinación de ocho posibles valores de verdad bajo cada variable proposicional, y estos valores de verdad los valores se pueden distribuir entre tres variables proposicionales en el siguiente orden. Si 'p', 'q' y 'r' son tres variables proposicionales de una proposición simbólica, entonces p tendría valores TTTTFFFF, q tendría valores TTFFTTFF y r tendría valores TFTFTFTF para determinar las funciones de verdad de la lógica principal. conectivo de la proposición simbólica. A continuación se muestra una ilustración de la tabla de verdad.
 16.25.24.png)
Entonces podemos aplicar la fórmula "2n" para determinar los posibles valores de verdad de la misma. En el caso de cuatro variables proposicionales de una proposición simbólica, podemos tener 24 = 16 valores de verdad posibles. En el caso de cinco variables proposicionales de una proposición simbólica, podemos tener 25 = 32 posibles valores de verdad, y así sucesivamente. En el caso de una variable proposicional y una conectiva lógica, para determinar su función de verdad, dibujamos una tabla de verdad que consta de dos filas y dos columnas. En el caso de dos variables proposicionales y una conectiva lógica (una proposición compuesta), para determinar sus funciones de verdad, dibujamos una tabla de verdad que consta de cinco filas y tres columnas. De esta manera, podemos sugerir que dependiendo del número total de variables proposicionales de una proposición simbólica, podemos averiguar la posible combinación de valores de verdad que tendría y, en consecuencia, podemos dibujar esas muchas filas en una verdad. tabla para determinar funciones de verdad del conectivo lógico principal de la proposición simbólica. Pero cuántas columnas se requieren para determinar la función de verdad del conectivo lógico principal de una proposición simbólica se basa en cuántas funciones de verdad de los conectivos lógicos necesitamos descubrir en la proposición misma. Las siguientes secciones determinan los valores de verdad de las proposiciones simbólicas adaptando el método de la tabla de verdad. Dibujaríamos las tablas de verdad para determinar las funciones de verdad de las conectivas lógicas de conjunción, disyunción, implicación y equivalencia seguidas de conectivas lógicas de daga y trazo.
1.36.6 La función conjuntiva y la función disyuntiva
Dos proposiciones simples unidas con y ’se conocen como proposición compuesta y conjuntiva. Por ejemplo, "Ram es un estudiante de lógica y Sita es una cantante". Esta proposición compuesta se simboliza como "p∧q". Dado que esta proposición simbólica tiene dos variables proposicionales y un conectivo lógico "∧", tiene una combinación de cuatro posibles valores de verdad para determinar la función de verdad de "p∧q". La función de verdad de "p∧q" se menciona a continuación mediante el método de la tabla de verdad.
 16.26.26.png)
La tabla de verdad muestra que la función conjuntiva "p∧q" es verdadera cuando tanto "p" como "q" son verdaderas. Si alguna de las variables proposicionales es falsa, entonces la función de verdad de la conjunción se vuelve falsa. En el caso de una función disyuntiva, una proposición compuesta se formula con una expresión de una o otra. Por ejemplo, “Cualquier Rogelio es un estudiante de lógica o María es una cantante". En la proposición disyuntiva, dos proposiciones simples están conectadas con un conectivo lógico "∨". La proposición compuesta disyuntiva se simboliza como "p∧q". Dado que esta proposición simbólica tiene dos variables proposicionales y un conectivo lógico "∨", tiene una combinación de cuatro valores de verdad posibles para determinar la función de verdad de "p∨q". La función de verdad de "p∨q" se coloca a continuación mediante el método de la tabla de verdad.
La tabla de verdad sugiere que una función disyuntiva es verdadera cuando al menos una de sus variables proposicionales es verdadera. Pero cuando ambas variables proposicionales son falsas, la función de verdad de la proposición disyuntiva es falsa.
1.36.7 Función implicativa y función de equivalencia
La implicación es un conectivo lógico que se conecta con las partes antecedente y consecuente de una proposición compuesta y se formula mediante la expresión "si-entonces". Por ejemplo, "Si viene a la clase de lógica, obtendrá los materiales del curso". Esta proposición compuesta se simboliza como "p → q". Dado que esta proposición simbólica tiene dos variables proposicionales y un conectivo lógico "→", tiene una combinación de cuatro posibles valores de verdad para determinar la función de verdad de "p → q". La función de verdad de "p → q" se menciona a continuación mediante el método de la tabla de verdad.
 16.29.31.png)
La tabla de verdad transmite que una función implicativa es falsa cuando el antecedente es verdadero y el consecuente es falso. En el resto de los otros casos, el valor de verdad de la función implicativa es verdadero. En el caso de una conectiva lógica de equivalencia, dos proposiciones atómicas se combinan con una expresión "si y sólo si". Es una proposición compuesta que se conecta con el conectivo lógico "≡". Por ejemplo, "Sus dedos se quemarán si y solo si juega con fuego". Esta proposición compuesta se simboliza como "p≡q". Dado que esta proposición simbólica tiene dos variables proposicionales y un conectivo lógico "≡", tiene una combinación de cuatro posibles valores de verdad para determinar la función de verdad de "p≡q".
La función de verdad de "p≡q" se ilustra en el método de la tabla de verdad.
 16.30.21.png)
La tabla de verdad establece que si ambas proposiciones son verdaderas, entonces la función de verdad de la equivalencia es verdadera. Además, si ambas proposiciones son falsas, entonces la función de verdad de la equivalencia también es verdadera. Pero si una de las proposiciones es verdadera y otra es falsa, entonces la función de verdad de equivalencia es falsa.10.8 Función de daga y función de trazo En el caso de la función de daga, una proposición compuesta se formula con la expresión "ni ni". Por ejemplo, "Ni es estudiante de ciencias ni de comercio". En esta proposición, dos proposiciones simples están conectadas con un conectivo lógico "↓". Esta proposición se simboliza como "p ↓ q". Dado que esta proposición simbólica tiene dos variables proposicionales y un conectivo lógico "↓", tiene una combinación de cuatro posibles valores de verdad para determinar la función de verdad de "p ↓ q". La función de verdad de "p ↓ q" se indica a continuación en un método de tabla de verdad.
 16.31.14.png)
La tabla de verdad expresa que cuando ambas proposiciones son falsas, la función de verdad de la daga es verdadera, y si una de las proposiciones es verdadera, entonces la función de verdad de la daga es falsa. La función de trazo se conoce popularmente como función de trazo de Sheffer. Es un conectivo lógico binario que se conecta con dos proposiciones simples y forma una proposición compuesta. Estos estados conectivos lógicos que no ambas proposiciones de una posición compuesta son verdaderas. Sugiere que al menos una de las proposiciones de dos proposiciones de la proposición compuesta debe ser falsa. La expresión no ambos 'en una proposición compuesta identifica que dos proposiciones simples se unen con la función de trazo. Por ejemplo, "No es tanto una silla como una mesa". Esta proposición compuesta se simboliza como "p | q ’. Dado que esta proposición simbólica tiene dos variables proposicionales y una conectiva lógica "|", tiene una combinación de cuatro posibles valores de verdad para determinar la función de verdad de "p | q ’. La función de verdad de "p | q ’se aclara a continuación mediante el método de la tabla de verdad.
 16.31.56.png)
La tabla de verdad transmite que cuando ambas proposiciones son verdaderas, la función de verdad del trazo de Sheffer es falsa, pero cuando una de las proposiciones es falsa, la función de verdad del trazo de Sheffer es verdadera. Resumamos las funciones de verdad de las conectivas lógicas binarias mediante el método de la tabla de verdad.
 16.32.41.png)
Esta tabla de verdad se presenta alternativamente de la siguiente manera.
Conjunción: ∧ = TT / T
Disyunción: ∨ = FF / F
Implicación: → = TF / F
Equivalencia: ≡ = TT / T y FF / T
Daga: ↓ = FF / T
Accidente cerebrovascular: | = TT / F
1.37 Valor de verdad: tautología, contradicción y contingente
Al determinar el valor de verdad de una proposición simbólica adoptando el método tabular de verdad, bajo la columna conectiva lógica principal, podemos encontrar que todos los valores son verdaderos o falsos o un combinación de verdadero y falso. Si la columna conectiva lógica principal contiene sólo valores "verdaderos", entonces decimos que el valor de verdad de la proposición es una tautología. Si contiene solo valores "falsos", entonces decimos que el valor de verdad de la proposición es lógicamente falso o contradictorio. Pero si contiene una combinación de valores verdaderos y falsos, entonces decimos que el valor de verdad de la proposición simbólica es contingente. Averigüemos el valor de verdad de las siguientes proposiciones simbólicas mediante el método tabular de verdad.
Ejemplo-1: {(~ q → ~ p) ≡ (p → q)}
La conexión lógica principal de esta proposición simbólica es "≡". Para averiguar el valor de verdad de la proposición simbólica, necesitamos contar cuántas variables proposicionales tiene esta proposición. Dado que la proposición tiene dos variables proposicionales, tendremos una combinación de cuatro posibles valores de verdad. Para averiguar los valores de verdad bajo la conectiva lógica principal, necesitamos averiguar la función de verdad de "(~ q → ~ p)" y "(p → q)". Además, para averiguar la función de verdad de "(~ q → ~ p)", necesitamos averiguar el valor de verdad de "~ q" y "~ p". El valor de verdad de "~ q" y "~ p" depende del valor de verdad de "q" y "p". Nuevamente, necesitamos averiguar la función de verdad de "(p → q)". Entonces, necesitamos tener siete columnas y cinco filas para averiguar el valor de verdad de la proposición simbólica a través del método tabular de verdad. La tabla de verdad se ilustra a continuación.
 16.34.36.png)
Bajo el conectivo lógico principal de la proposición simbólica, encontramos los valores de verdad TTTT. Por tanto, la proposición es lógicamente verdadera y, por tanto, tautología.
Ejemplo-2: {(p → q) ∨ (~ (p ≡ ~ q))}
Esta proposición simbólica tiene dos variables proposicionales, "p" y "q". Por tanto, tendremos una combinación de cuatro posibles valores de verdad. La conexión lógica principal de la proposición simbólica es "∨". Para averiguar el valor de verdad de la proposición simbólica, necesitamos averiguar la función de verdad de "(p → q)" y "(~ (p ≡ ~ q))". Para averiguar la función de verdad de "(~ (p ≡ ~ q))", necesitamos averiguar el valor de verdad de ~ q y la función de verdad de "(p ≡ ~ q)". Teniendo en cuenta el conectivo lógico de una proposición compuesta, necesitamos dibujar la tabla de verdad. La tabla de verdad se presenta a continuación.
 16.35.25.png)
Bajo el conectivo lógico principal de la proposición simbólica, encontramos los valores de verdad de TFTT. Es una combinación de valores verdaderos y falsos. Por tanto, la proposición simbólica se considera contingente.
Ejemplo-3: {(p ∧ (~ q → p)) ∧ ~ ((p ≡ ~ q) → (q ∨ ~ p))}
Esta proposición simbólica tiene dos variables proposicionales "p" y "q". Entonces, podemos tener una combinación de cuatro posibles valores de verdad. La conexión lógica principal de la proposición es "∧". Para determinar el valor de verdad de la conectiva lógica principal de la proposición simbólica, necesitamos encontrar la función de verdad de '(p ∧ (~ q → p))' y '~ ((p ≡ ~ q) → (q ∨ ~ p)) '. Además, para averiguar la función de verdad de "(p ∧ (~ q → p))", necesitamos averiguar el valor de verdad de ~ q y la función de verdad de "(~ q → p)". Nuevamente, para averiguar la función de verdad de '~ ((p ≡ ~ q) → (q ∨ ~ p))', necesitamos averiguar el valor de verdad de ~ p y la función de verdad de '(p ≡ ~ q) 'y' (q ∨ ~ p) '. Ahora, necesitamos poner todas las proposiciones simples, proposiciones compuestas y proposiciones complejas en las columnas de la tabla de verdad para determinar el valor de verdad de toda la proposición simbólica. La siguiente tabla de verdad ilustra el valor de verdad de la proposición simbólica.
Bajo el conectivo lógico principal de la proposición simbólica, encontramos valores de verdad FFFF. Por tanto, el valor de verdad de la proposición simbólica se considera contradictorio. Hemos discutido el método de la tabla de verdad en detalle y analizado el procedimiento para determinar la función de verdad de una proposición simbólica. También explicamos las condiciones bajo las cuales una proposición simbólica sería tratada como tautología, contradicción y contingente. Pero se encuentra que si una proposición simbólica tiene más de dos variables proposicionales y algunas conectivas lógicas, entonces no sería un ejercicio agradable determinar su función de verdad a través del método tabular de verdad, ya que habría muchas columnas y muchas filas. Por lo tanto, los lógicos adoptaron un método indirecto de procedimiento de decisión de tabla de verdad para determinar la función de verdad de proposiciones simbólicas complejas.
 16.37.59.png)
[1] https://elpais.com/ciencia/2025-01-21/licia-verde-astrofisica-en-la-ciencia-hay-que-saber-apreciar-el-recorrido-y-no-solo-las-respuestas.html
[2] Strawson, G. (2009) Selves: An Essay in Revisionary Metaphysics, Oxford: Oxford University Press.
[3] Sellars, W. S. (1963/1991) Science, Perception and Reality, Atascadero, CA: Ridgeview Publishing Co.
[4] Fichte, J. G. (1794–5/2021) J. G. Fichte: Foundation of the Entire Wissenschaftslehre and Related Writings, 1794–95, trans. D. Brezeale, Oxford: Oxford University Press.
[5] Daniel C. Dennett (2023) I’ve Been Thinking. W. W. Norton & Company
[6] Arturo Schopenhauer (2010) El Arte De Tener Razon. Alianza
[7] Bas C. van Fraassen (1989) Laws and Symmetry. Clarendon Press
[8] Hartmann, Stephan & Bovens, Luc. (2003). Bayesian Epistemology.
[9] Giovanni Boccaccio (2017) The decameron. Penguin Clásicos.
[10] Kim, Hyoju & Tomblin, J. & Mcmurray, Bob. (2024). Speech Categorization Consistency Predicts Overall Language Abilities. 10.31234/osf.io/u46pj.
[11] Lombrozo, Tania & Gwynne, Nicholas. (2014). Explanation and inference: mechanistic and functional explanations guide property generalization. Frontiers in Human Neuroscience. 8. 700. 10.3389/fnhum.2014.00700.
[12] DeJong, Gerald & Bennett, Scott. (1995). Extending Classical Planning to Real-World Execution with Machine Learning.. 1153-1161.
[13] Woodward, James. (2021). Experimental Results Concerning Invariance: Cheng, Lombrozo, and Others. 10.1093/oso/9780197585412.003.0008.
[14] Jern, Alan & Derrow-Pinion, Austin & Piergiovanni, AJ. (2021). A computational framework for understanding the roles of simplicity and rational support in people's behavior explanations. Cognition. 210. 104606. 10.1016/j.cognition.2021.104606.
[15] Bovens, Luc & Hartmann, Stephan. (2005). Coherence and the Role of Specificity: A Response to Meijs and Douven. Mind. 114. 10.1093/mind/fzi365.
[16] Beierle, Christoph & Kern-Isberner, Gabriele. (2021). Selection Strategies for Inductive Reasoning From Conditional Belief Bases and for Belief Change Respecting the Principle of Conditional Preservation. The International FLAIRS Conference Proceedings. 34. 10.32473/flairs.v34i1.128459.
[17] Jacobs, Struan. (1991). John Stuart Mill on Induction and Hypotheses. Journal of the History of Philosophy. 29. 69-83. 10.1353/hph.1991.0008.
[18] Harman, Gilbert. (2017). La inferencia a la mejor explicación. Euphyía - Revista de Filosofía. 3. 143. 10.33064/4euph50.
[19] Shebilske, Wayne & Rock, Irwin. (1986). The Logic of Perception. The American Journal of Psychology. 98. 151. 10.2307/1422773.
[20] Hohwy, Jakob. (2016). The Diversity of Bayesian Explanation. 10.7551/mitpress/10603.003.0060.
[21] Magnani, Lorenzo. (2002). An Adductive Theory of Scientific Reasoning.. 1226-1232.
[22] Dellsén, Finnur. (2024). Abductive Reasoning in Science. Elements in the Philosophy of Science. 10.1017/9781009353199.
[23] Stilgenbauer, Jean-Louis & Baratgin, Jean & Douven, Igor. (2017). Reasoning strategies for diagnostic probability estimates in causal contexts: Preference for defeasible deduction over abduction. https://www.researchgate.net/publication/317847835_Reasoning_strategies_for_diagnostic_probability_estimates_in_causal_contexts_Preference_for_defeasible_deduction_over_abduction?_sg=4vN8h0KHd2_E5q9RqxGk5ZbpJM_sf0sAySLIRucv_NCHBdOZ5HrVAt8lJl8QHy6Z3u4zkToQKWuwe6k&_tp=eyJjb250ZXh0Ijp7ImZpcnN0UGFnZSI6Il9kaXJlY3QiLCJwYWdlIjoiX2RpcmVjdCJ9fQ
[24] Barés-Gómez, Cristina & Fontaine, Matthieu. (2024). The logic of medical discovery: the case of Jenner’s inquiry on variolae vaccinae. Logic Journal of the IGPL. 10.1093/jigpal/jzae084.
[25] Richard McElreath (2020) Statistical Rethinking: A Bayesian Course with Examples in R and STAN. Chapman and Hall/CRC
[26] Eli de Gortari (2016) La ciencia en la historia de México. FCE
[27] Alex Rosenberg, The Atheist’s Guide to Reality: Enjoying Life without Illusions (New York: Norton, 2011).
[28] Crupi, Vincenzo & Calzavarini, Fabrizio. (2023). Critique of pure Bayesian cognitive science: A view from the philosophy of science. European Journal for Philosophy of Science. 13. 10.1007/s13194-023-00533-w.
[29] McLatchie, Yann & Vehtari, Aki. (2024). Efficient estimation and correction of selection-induced bias with order statistics. Statistics and Computing. 34. 10.1007/s11222-024-10442-4.
[30] Szreder, Miroslaw. (2022). Noise and bias – some controversies raised by the book ‘Noise: A Flaw in Human Judgment’, written by Daniel Kahneman, Olivier Sibony, Cass R. Sunstein. Przegląd Statystyczny. 69. 39-49. 10.5604/01.3001.0015.8792.
[31] Sleptsova, Yulia & Kachalov, Roman & Shokin, Yan. (2024). Risk factors for cognitive biases when making management decisions. Economics of Contemporary Russia. 125-139. 10.33293/1609-1442-2024-2(105)-125-139.
[32] Brennan, Geoffrey et al., (2013). Explaining Norms (Oxford University Press)
[33] Ehrlinger, Joyce & Gilovich, Thomas & Ross, Lee. (2005). Peering Into the Bias Blind Spot: People’s Assessments of Bias in Themselves and Others. Personality & social psychology bulletin. 31. 680-92. 10.1177/0146167204271570.
Mavrogiorgos, Konstantinos & Kiourtis, Athanasios & Mavrogiorgou, Argyro & Menychtas, Andreas & Kyriazis, Dimosthenis. (2024). Bias in Machine Learning: A Literature Review. Applied Sciences. 14. 8860. 10.3390/app14198860.
Shanks, David & Coles, Hollie & Yeo, Nadia. (2024). A re-evaluation of gender bias in receptiveness to scientific evidence of gender bias. Royal Society Open Science. 11. 10.1098/rsos.240419.
[34] Salim, Emil. (2022). Kvanvig on Reducing Personal to Doxastic Justification. Philosophia. 50. 10.1007/s11406-021-00394-8.
[35] Meshkibaf, Fatemeh & Khazaei, Zahra & Legenhausen, M. (2023). Epistemic Luck and Anti-Luck Epistemology in the View of Duncan Pritchard. 25. 5-32. 10.22091/JPTR.2023.9322.2878.
[36] Hetherington, Stephen. (2024). Stephen Hetherington on Epistemology: Knowing, More or Less. 10.5040/9781350344778.
[37] Kulic, Anthony. (2010). Michael Strevens. Depth: An Account of Scientific Explanation. Spontaneous Generations: A Journal for the History and Philosophy of Science. 4. 10.4245/sponge.v4i1.14195.
[38] Legg, Catherine (2024) Interpreting Sellars: Critical Essays. Cambridge University Press
[39] Griffith, Aaron. (2025). Truth and Truthmaking. 10.1093/9780198948469.003.0002.
[40] Stanovich, Keith & West, Richard & Toplak, Maggie. (2013). Myside Bias, Rational Thinking, and Intelligence. Current Directions in Psychological Science. 22. 259-264. 10.1177/0963721413480174.
Stanovich, Keith & Toplak, Maggie & West, Richard. (2021). Rationality and Intelligence. 10.7551/mitpress/11252.003.0087.
[41] Stanovich, Keith. (2021). The Bias That Divides Us: The Science and Politics of Myside Thinking. 10.7551/mitpress/13367.001.0001.
[42] Stevens, Christopher & Lacroix, Cathy & Bouchet, Mathilde & Marsicano, Giovanni & Marighetto, Aline. (2024). Mice-side bias: Deliberative decision making in a model of rule revision reveals ‘myside’ confirmation bias-like cognitive processes in mice. 10.1101/2024.12.03.626648.
[43] Jeklic, Mihael. (2024). Suppressing Myside Bias in Civil Litigation. Law and Human Behavior. 48. 564-579. 10.1037/lhb0000584.
[44] Rachev, Nikolay. (2021). Myside Bias, School Performance, and the Polarity of Music Preferences. Journal of Cognitive Psychology. 33. 77-86. 10.1080/20445911.2020.1841778.
[45] Kuhn, Deanna & Modrek, Anahid. (2017). Do reasoning limitations undermine discourse?. Thinking and Reasoning. 1-20.
[46] Bolsen, Toby & Palm, Risa. (2019). Motivated Reasoning and Political Decision Making. 10.1093/acrefore/9780190228637.013.923.
[47] Diakidoy, Irene-Anna & Christodoulou, Stelios & Floros, Georgios & Iordanou, Kalypso & Kargopoulos, Philip. (2015). Forming a belief: The contribution of comprehension to the evaluation and persuasive impact of argumentative text. British Journal of Educational Psychology (2015), 85, 300–315
[48] Macpherson, Robyn & Stanovich, Keith. (2007). Cognitive ability, thinking dispositions, and instructional set as predictors of critical thinking. Learning and Individual Differences. 17. 115-127. 10.1016/j.lindif.2007.05.003.
[49] Zhang, Sirui. (2025). Analysis and optimization of the applicability of hypothesis testing methods. Advances in Operation Research and Production Management. 4. 75-78. 10.54254/3029-0880/2025.24261.
[50] Evans, J. St. B. T. 2017. Belief bias in deductive reasoning. In R. Pohl, ed.. Cognitive illusions, 2nd ed., 165–181. London: Routledge.
[51] Carson, Thomas (2010) Lying and deception: theory and practice. Oxford University Press.
[52] Williams, Bernard (2002) Truth and Truthfulness. Priceton university Press
[53] Greene, J. and J. Paxton (2009) Patterns of neural activity associated with honest and dishonest moral decisions. PNAS 106: 12506-12511.
[54] Shepherd, Dean & Wincent, Joakim & Chase, Sarah. (2025). What if we are the WEIRD Ones? A Call (and Roadmap) for More Non-WEIRD Entrepreneurship Research. Entrepreneurship Theory and Practice. 49. 10.1177/10422587251347051.
[55] Roberts, Robert. (2025). Generosity and Gratitude. 10.1017/9781009570916.006.
[56] Bubel, Martin & Seufert, Philipp & Karpov, Gleb & Schwientek, Jan & Bortz, Michael & Oseledets, Ivan. (2025). Optimal experimental design: from design point to design region. Statistical Papers. 66. 10.1007/s00362-025-01725-7.
[57] Mariel, Petr & Campbell, Danny & Sandorf, Erlend & Meyerhoff, Jürgen & Vega Bayo, Ainhoa & Blevins, Rebecca. (2025). Experimental Design. 10.1007/978-3-031-89338-4_5.
[58] Simons, Daniel & Shoda, Yuichi & Lindsay, D.. (2018). Constraints on generality statements are needed to define direct replication. Behavioral and Brain Sciences. 41. 10.1017/S0140525X18000845.
[59] Niebles, Mario. (2023). La Teoría de los Sistemas Ecológicos de Urie Bronfenbrenner como marco para comprender la deserción universitaria. Collectivus, Revista de Ciencias Sociales. 10. 10.15648/Collectivus.vol10num2.2023.3823.
[60] Clarke, Bridget. (2008). Thomas Stringer, Locke, Shaftesbury, and Edward Clarke. Locke Studies. 8. 171-199. 10.5206/ls.2008.1014.
[61] Julius, Arinaitwe. (2025). The Shifting Sands of Knowing: Evaluating the Evolution of Knowledge Since Plato and Gettier. 9. 246-252.
[62] Kreiser, Lothar. (2001). Gottlob Frege. DOI:10.28937/978-3-7873-2513-9.
[63] Riffert, Franz. (2009). Alfred North Whitehead.
DOI:10.30965/9783657768387_178.
[64] Mitchell, David. (2019). An Introduction to Logic.
DOI:10.4324/9780367854195.
[65] Orey, Steven & Basson, A. & O'Connor, D.. (1962). Introduction to Symbolic Logic.. Journal of the American Statistical Association. 57. 263.
DOI:10.2307/2282488.
[66] Woleński, Jan. (1987). Alfred Tarski as a philosopher. Annales Societatis Mathematicae Polonae. Seria II. Wiadomości Matematyczne. 27.
[67] Morrill, Glyn & Fowler, Timothy. (2011). Categorial Grammar: Logical Syntax, Semantics, and Processing.
[68] Whitehead, A. & Russell, B.. (2021). Principia Mathematica. Vol I. 2nd ed.
[69] Baldwin, Thomas. (2021). C. I. Lewis. DOI:10.4324/9781315204369-9.
[70] Sochacki, Robert. (2021). Logical Sentential Calculi Inspired by the Chrysippean Sentential Calculus.
DOI:10.1007/978-3-030-72254-8_16.
