Primer semestre: Pensamiento aritmético

2.1 ¿Qué es un número? 

Al igual que las obras literarias, las obras matemáticas nos ayudan a expandir nuestro círculo de empatía, liberándonos de la tiranía de un único punto de vista. Los números, debidamente considerados, nos hacen mejores personas. Por ejemplo, al pensar en los muchos puntos que infinitamente pueden dividir el espacio de nuestro corazón. Utilizamos a los números para dar sentido a nuestra realidad. Nos dicen cuantas categorías de cosas hay en nuestro alrededor. La hora en que veremos a alguien para conversar en un café. La edad que tendremos al egresar de la universidad. La cantidad de sal para cocinar unos chilaquiles. La distancia a la que está nuestra casa de la escuela. La velocidad de nuestra bicicleta. El número de hermanos que tenemos. Lo pequeño que somos comparados con las estrellas en el cielo. Nos ayudan a entender como invertimos nuestro tiempo, dinero y vida. En fin, los números los hay enteros, decimales, reales, imaginarios, irracionales, racionales, negativos, positivos, primos, y ellos están dentro de la toma de decisiones (probabilidad); en la medida de las dimensiones del espacio (geometría); en la cuenta de elementos de categorías (conjuntos); para identificar la unidad en las capas de la realidad (mónada); para realizar cálculos (lógica).  

El rechazo de Aristóteles al pensamiento matemático fue antitético a la filosofía de su maestro Platón. Por otro lado, Pitágoras estudio aritmética, geometría, música y astronomía y postuló que los números enteros eran cruciales, por su notable capacidad para explicar, por ejemplo, los armónicos musicales y las propiedades de los objetos geométricos. La escuela pitagórica aseguro que los números enteros eran esenciales para una comprensión fundamental de la forma en que el universo está diseñado. Platón considero a las matemáticas fundamentales para hacer filosofía y que la geometría llevaría a la comprensión del mundo. Sin embargo, es Euclides quien introduce nuevos estándares de rigor al pensamiento matemático^[1]. El libro de Euclides “Elementos” se convirtió en el texto más influyente durante siglos, Einstein comento al respecto: “si Euclides no encendió tu entusiasmo en la juventud, entonces no naciste para ser científico^[2]”. La idea de las regularidades en el comportamiento de los objetos que los humanos observamos en la Tierra, se pensó desde Arquímedes, eran descritas por leyes matemáticas. Este fue el primer paso de hacer trascender los sentidos humanos, es decir, al desplegar el poder de la razón imaginativa, con la mirada levantada a los objetos en el cielo.  

Para comprender las ideas matemáticas, la biología y su ciencia cognitiva están interesadas en dar respuestas en el cómo los individuos entienden, aumentan su rendimiento y por qué algunos encuentran tantas dificultades en su aprendizaje matemático. La neurociencia, la genética y la psicología están conjuntando esfuerzos en el estudio de la subitización^[3]. A la competencia matemática que se presenta como un desarrollo temprano de la habilidad numérica se le llama subitización y conteo. La primera, refiere a la numeración de elementos entre 1 y 4 dado por reconocimiento de patrones. El conteo además de hacerlo uno a uno, asigna símbolos dentro de un sistema numérico^[4]. 

Subitización es un término científico que refiere a la habilidad de identificar y numerar objetos, sin error, rápidamente y exacto. Se cree que es la base del mismo mecanismo del conteo^[5]. La acción de numerar es la habilidad de crear el valor total de un conjunto de elementos y la habilidad innata de numerar una cantidad pequeña de 1 a 4 en 250 milisegundos sin contar y libre de errores; a esto, los biólogos desde 1941 le nombraron subitización^[6]. Subitización no es estimar una cantidad, sino un conocimiento de un patrón intuitivo^[7], es preverbal, una cantidad concreta visual espacial. El conteo y la subitización solo pueden darse cuando se une la información visual de los objetos y se localiza a la unidad dentro de ellos^[8]. 

La memoria de trabajo es un sistema necesario para acumular actividades complejas de conteo de grandes números^[9], se especula que allí existe un buffer de acumulación secuencial, conformado por los mecanismos de focalizar la unidad (mónada) dentro de un conjunto de elementos, la capacidad de subitar y la visión espacial, todos ellos juegan a favor de desarrollar mayor complejidad en los rangos de una cuenta, pero son procesos diferentes^[10]. El conteo es un proceso articulado en el buffer de manera serial y de acumulación simultánea, la subitización es más exacta, rápida y permite en pequeños rangos ganar exactitud en modo de tramos de numeración no simbólica. El conteo es ya un proceso simbólico con un rol de intención de cálculo de rangos mayores a 4 elementos y que permite llegar a grandes numeraciones. Además diferenciemos, el conteo es una estimación, un proceso de probabilidad de cálculo por subitización, el cual es inexacto y con errores siempre presentes en sus determinaciones.

Un número implica para su comprensión ideas de las disciplinas pedagógicas neuronales y matemáticas en procesos subyacentes de aprendizaje, es la cognición matemática empleada por los individuos para reconocer que en la realidad hay patrones numéricos. Se estima que el 24% de los adultos tienen dificultades para realizar cálculos de numeración equivalentes a niveles inferiores a los establecidos en niños de 8 años, se refiere en cálculos de conteos, fraccionarios, porcentajes y manejo de decimales^[11]. Los científicos creen que el aprendizaje desde las capas subyacentes de la base biológica de los axiomas, permite más eficazmente aprender a identificar las ideas matemáticas que son cimientos y en consecuencia, mejora la abstracción del pensamiento matemático en todos aquellos que batallan con este tipo de conocimiento^[12].

El rendimiento matemático está implicado con la aplicación formal de sistemas de representación simbólica con bajo contacto intuitivo de los axiomas de unidad, espacio geométrico, probabilidad, lógica y categorización. Los sistemas simbólicos representan ideas matemáticas que los estudiantes deben relacionar con la vida cotidiana justo antes de las estructuras formales simbólicas, esta pedagogía de las matemáticas es el paradigma proceptual-simbólico^[13]. 

¿Qué es realmente un número? ¿Existen números como objetos abstractos independientes del lenguaje humano? ¿Son objetos lógicos construidos dentro de un sistema axiomático dado como lo sugieren los formalistas? O son simplemente etiquetas generadas por un sistema numérico para referir a tipos de cantidades o conjuntos. Otros, los más recientes en la escena científica, refieren a número como el resultado de habilidades innatas de la cognición matemática^[14]. La cognición matemática ha descubierto procesos implicados en la comprensión de las ideas matemáticas y la forma de representación numérica en la aritmética. Es claro que los niños lactantes son capaces de procesar información numérica antes de aprender su representación simbólica. Este proceso innato de numerar y reconocer a la unidad dentro de las capas subyacentes de la realidad, permite a los niños desarrollar en adelante habilidades formales del pensamiento matemático. La subitización ha demostrado que la actividad de numerar está antes de que se conecten la palabra con número y símbolo dentro de un sistema numérico. Una vez que se aprende el sistema generador de números, los niños empiezan a usarlos en operaciones aritméticas.

La verdadera competencia aritmética desarrolla la idea de operador numérico de adición, sustracción, multiplicación y división; pero se requiere el conocimiento básico de número dentro de un entrenamiento formal del sistema simbólico numérico. Comprender lo que es un operador, nos ayuda a relacionar lo que es una operación aritmética al elegir las estrategias adecuadas para su cálculo. La memoria de trabajo se expande y la atención racional se agudiza para reflexionar la habilidad intelectual de numerar, estimar y el conteo de numerales grandes. Numeral lo referimos a la representación simbólica de número, pero en adelante unificamos la idea en simplemente número, como dos dimensiones, una refiere a patrones subitizar de cantidad y otra a un sistema numérico simbólico formal. 

Los números racionales requieren que los niños vayan más allá de la lista de una cuenta de indexar símbolos con cantidades y en referencia profunda a la idea de mónada. Resultan estos números desafiantes para muchos adultos que dentro de las universidades reflejan una baja habilidad cognitiva para su manejo en operaciones aritméticas con racionales. Es necesario que las representaciones simbólicas de números, operadores y signos sean reconocidos desde las ideas intuitivas justo antes de mayores abstracciones simbólicas. Lo proceptual refiere a un aprendizaje que valora como condición inicial, la habilidad de reconocer el significado matemático encapsulado en los símbolos. El pensamiento matemático es habilidad de comprensión (saber por qué: proceptual) y habilidad procedimental (saber cómo hacerlo: sistema simbólico formal).

A los matemáticos les tomó mucho tiempo llegar a preguntarse cuál fue la respuesta y mucho más tiempo para encontrar un número. El primer paso fue caracterizar a los números naturales. Resultó que su rasgo definitorio más importante no fue la noción de cantidad o su aritmética dentro del concepto de álgebra. Sino la prueba por inducción, por ser una mirada más profunda en su sustancia.

Proposición: La suma de los primeros números n naturales es:

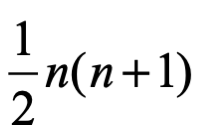
Demostración: Esto es verdadero trivial para n=1. Si bien es cierto

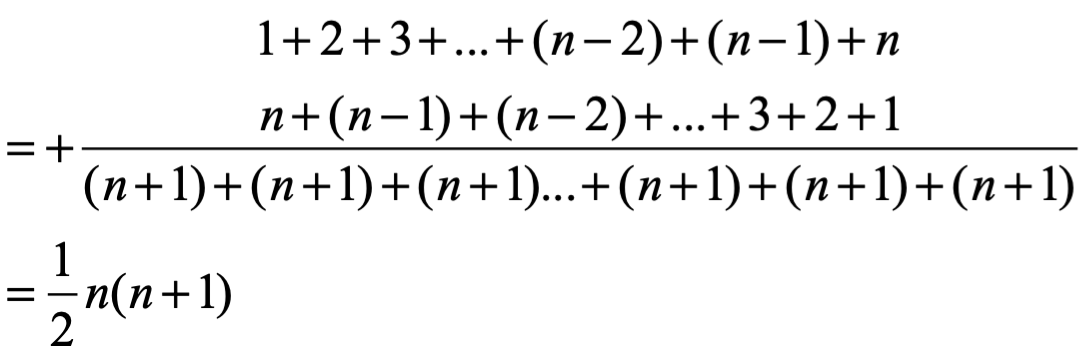
Es decir, dos series infinitas una creciente y otra decreciente las sumamos, luego factorizamos (n+1) y dividimos entre dos, y encontramos la suma total de los números naturales.

Muchos consideran este tipo de demostración como un argumento de prueba de verdad, se establece el estado de la proposición como verdadero. El único problema con esta forma de pensar es que llegar a valores grandes de n requiere de un gran número de aplicaciones de pasos en general. Nunca podremos cubrir todos los números naturales en un infinito de deducciones si procedemos un caso a la vez. Pero una demostración, por definición, se compone de un número finito de líneas de cláusulas hipotéticas deductivas sobre el universo de posibilidades.

La salida a este dilema es eliminar la parte de y así sucesivamente de pruebas por casos repetitivos, de una demostración. Demostrar por inducción entonces es hacer encajar un extenso número de casos (proposiciones) en un tipo de prueba como y así sucesivamente. Un número por deducción e inducción apunta directamente a la definición de número natural.

A los números verbales los llamamos simplemente números y a los escritos numerales. Al referirnos a las cantidades abstractas descritas por los números, nosotros utilizamos símbolos como 1,2,3,4,5,6…, y así sucesivamente. Investigadores lingüistas, antropólogos, psicólogos, biólogos y otros, están creando una nueva historia para los números. Algunos son partidarios de considerar a los números como conceptos que no vienen a las personas de manera innata o natural. Es decir, así como la escritura y la lectura alfabética no son naturales, sino de creación cultural. Los números están ausentes de algunas poblaciones del mundo. La noción de contar es parte del perfil de nuestra especie, dada por un acumulador cerebral para reconocer el paso del tiempo, pero para la noción de número, para esta última es necesario ser educado. El número o numeral, aquí lo referimos indistinto mientras no especifiquemos lo contrario. El número es uno de los inventos claves en el curso de nuestra civilización, vive como una especie de piedra pedernal que encendió la línea de tiempo humana cuando se percibe al universo entero como una estructura de números.

Tal vez la mejor manera de conocer este invento llamado número, es partir de reconocer en nuestro cerebro una habilidad sustancial, la de registrar el paso del tiempo. Pero tal vez, contar el tiempo desarrolló que apreciáramos patrones repetitivos de los ciclos de las estaciones. Es evidente que nuestra percepción del tiempo pasa por el papel de número en nuestra reflexión. ¿Qué significa percibir o sentir el tiempo? El tiempo es percibido en términos culturales, una especie de consenso de la experiencia cultural de una sociedad. A menudo los humanos de cualquier cultura reconocen el paso del tiempo, en términos de algo que pasó. El tiempo no es un parámetro de movilidad lento o rápido, el tiempo no se mueve realmente, no pasamos a través de él. Los científicos cognitivos establecieron hace tiempo que los seres humanos tienen una tendencia generalizada a utilizar especialmente cosas concretas, como los objetos materiales. Es decir, asumimos al tiempo como algo objetivo y parte del mundo material de nuestra vida. Así, sí nuestra vida cambia, es hablar de movimiento usando el paso por momentos de la existencia y siendo incapaces de volver en la dirección presente-pasado. Es a través de nuestra conciencia cerebral que enfrentamos el futuro como pasado en potencia a través de nuestro acumulador neuronal que registra una porción progresiva de cantidades. El habla humana es evidencia de las expresiones del tiempo, de cómo lo sentimos, por ello podemos hablar en presente, pasado y futuro, incluso desaparecer al tiempo. La mayoría de los humanos, percibimos el paso del tiempo en la manera en que contamos, escribimos y leemos^[15]. La música podemos verla como otro sistema artificial que el hombre inventó, reconociendo en ella las sensaciones del tiempo.

En la base espacial numérica, podemos reconocer las formas flexibles de pensamiento evidente, en el cómo consideramos cantidades naturales en una línea de tiempo. Es decir, consideramos las cantidades a la izquierda (pasado) y la derecha (futuro) y el presente metafóricamente instante de existencia. Así la cultura creó calendarios, barras de progreso en descarga de archivos “PDF”, líneas de tiempo en los libros de historia y así sucesivamente. Y hay sólida evidencia científica que sugiere que las prácticas simbólicas por defecto impactan en el cómo percibimos al tiempo. Los científicos observan que al pedir a un grupo de personas que organicen un conjunto de fotografías, tienden siempre a colocarlas de izquierda a derecha en el sentido temporal que ellas infieren^[16]. 

Estas pruebas reflejan un punto importante, apostamos a que el tiempo es una práctica cultural y lingüística, como resultado del acumulador que registra el paso del tiempo. Y aquí es donde nace la historia del número, como un símbolo que afecta todas las nociones de nuestra existencia. Los números naturales poseen la dirección del tiempo percibido, son los números claros obtenidos del pensamiento del movimiento del tiempo. Si pensamos al tiempo como algo que fluye, moviéndose a lo largo de la línea de tiempo frente a nosotros, su paso es contable, divisible y misterioso en cuanto a su límite. Piense en barras de progreso de descargas de archivos informáticos, la realidad, es que hay eventos que requieren ciertos procesos que consumen tiempo antes de que se manifieste un cambio significativo, los números naturales quizá fueron estos cambios significativos, donde la unidad es el mínimo cambio detectable al paso del tiempo. Esta conceptualización centrada en el número como paso de tiempo podría decirse que rige nuestra vida.

¿Qué hora es al momento que realiza esta lectura? Para nosotros, son las 13:51 al momento en que escribimos estas palabras en el occidente mexicano. Puesto que en este momento del día estoy en mi oficina, en mi escritorio, y no en mi casa. Qué significa esto, 13 horas y 51 minutos contados desde la media noche, en realidad nuestra experiencia mental es numérica. Son los números resultado de crear un medio para cuantificar nuestra existencia, dividir metafóricamente el paso del tiempo en unidades manejables para planear nuestra vida. Son un indicador del hecho de que los seres humanos en algún momento decidieron cuantificar momentos de tiempo de la experiencia. El tiempo puede ser real, existe además de nuestra experiencia, pero el número es una invención para relacionarnos con el mundo. De hecho, cuando respondemos sobre ¿qué hora es?, contestamos lingüísticamente con una tradición cultural que adoptó un sistema antiguo de numeración.

Al considerar la división de cada una de las rotaciones de la tierra, cada día, en 24 horas. ¿Por qué se dividió de este modo? No hay ninguna motivación astronómica en esta división. Después de todo, en teoría podría ser dividida un día sobre cualquier número. Fueron los egipcios los que para sus relojes de hace 3 mil años dividieron la luz del día en doce partes iguales. De esta división de la luz en el transcurso del día nace una tradición cultural apropiada para su sentido de la existencia. Así de esta manera, la unidad de tiempo para los relojes, fue el número 12, así la base numérica de la sensación del paso del tiempo para la luz del día fue duodecimal. Los sistemas de numeración, hay muchos de ellos, basados en muchas cosas diferentes. Sin embargo, para nosotros hoy, el sistema duodecimal está muy arraigado para contar el paso del tiempo, impone una cierta perspectiva en nuestro día a día. Nuestra vida cotidiana está gobernada por números para las horas, minutos y segundos. Pero en realidad el tiempo no ocurre en estas u otras unidades discretas. La segmentación del tiempo es contable en unidades producto de la mente humana^[17].

Contar el tiempo, es una necesidad que impulsó al hombre a crear la noción de número natural, sistema de numeración y gobierna las conductas sociales de nuestra civilización. Inventar al número como depositario de cantidad, pasó desde luego por la noción cultural de unidad de cantidad o mónadas como Leibniz las nombró. Esta idea abstracta de unidad, es el antecedente más relevante de nuestra especie para dar orden temporal a nuestro plan de vida. La unidad, es el concepto esencial e íntimo vinculado a la historia de los números.

El registro fósil sugiere que los homínidos, fueron capaces de registrar cantidades bajo el concepto de unidad. Los humanos modernos tenemos unos 100 mil años que surgimos, debemos aceptar que no fuimos nosotros los que descubrimos la unidad, pero sí fuimos nosotros los que con esta abstracción desarrollamos el invento de número. En el cruce temporal entre homínidos y humanos, allí está  el origen del número^[18]. Quizá una forma razonable, es que los Homo sapiens en su competencia por sobrevivir, intentaron descifrar los primeros registros rupestres de las cuevas de los homínidos. Así aprendimos la idea de unidad, como abstracción de algo necesario para establecer una cuenta de registro. La unidad fueron semillas, patos, caballos, hombres,… a menudo la unidad fue algo útil para que el registro fuera una memoria útil. Este cambio cognitivo es evidente, en la fabricación de tecnología de puntas de flecha, herramientas de hueso, quizá la teoría de supremacía del Homo sapiens sobre sus parientes más cercanos, es que la abstracción de la unidad a número en una cuenta natural, fue determinante para tomar ventaja tecnológica^[19]. 

De esta historia, podemos aprender, que las sociedades con mayor dominio matemático, son las que más poder acumulan y se hacen valer en forma de dominio tecnológico. Planear una guerra, es hacer uso del más sofisticado conocimiento matemático, solo baste ver el resultado del proyecto “Enigma” que decidió el rumbo de la segunda guerra mundial. Alan Turing fue el principal responsable de descifrar Enigma, el código secreto utilizado por el ejército alemán en la Segunda Guerra Mundial, contribuyendo con ello a acortar la guerra. Inventó una máquina, que permitía descifrar mensajes de Enigma de forma masiva, así nació la guerra cibernética, impulsada por avances matemáticos en materia de cifrado y codificación de códigos. Quizá lo que los Homo sapiens lograron, fue descifrar la noción de unidad de los homínidos, y tomar ventaja similar a lo hecho por Alan Turing para ganar la guerra.

La historia del número, es la misma explicación que nos hace lingüísticos por actos de invención y creación de sistemas alfabéticos y numéricos. Esta creación, es decir, invenciones no naturales, nos dieron la habilidad de comunicar, cooperar y organizar colectivamente el poder del conocimiento, transmitiendo por símbolos mensajes al futuro, haciendo portable la información y creando un arte de números y letras, que a la postre desarrollaron la civilización de manera espectacular^[20]. Pero tenga presente, que la noción de número a partir de la idea de unidad, creó las bases de todo el sistema de numeración moderno. 

Como conclusión parcial, un número es un símbolo dentro de un sistema numérico construido bajo las nociones de registro del tiempo y unidad (cantidad), donde es resultado de una tradición cultural que ha elegido una base numérica como patrón representativo de la existencia humana. El número está como noción innata en nuestra biología. 

2.2 Contar números 

Desde tiempos tempranos del hombre en la tierra, surge la necesidad de contar, hacer un registro de animales, frutas, guerreros y muchas cosas más. Para ello emplearon pilas de piedras, marcas en huesos, palos de madera y dedos de las manos que al paso del tiempo se convirtieron en la base del sistema numérico de base 10. Los Mayas emplearon la base 20, y en Mesopotamia la base 60. 

La unidad como abstracción matemática en todas las culturas fue desarrollada. La unidad para la noción de un símbolo que asocia cantidad dentro de un sistema numeral fue fundamental, así el número es la base de contar. En nuestro familiar sistema decimal, basado en el número 10, se escriben los números posicionándose en columnas separadas para las unidades (1), diez (10), cientos (100), miles (1000)…, a medida que avanzamos de derecha a izquierda. El conjunto de símbolos de este sistema son 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Este sistema de valor refleja las cantidades asociadas colocando cada símbolo en su columna, multiplicando por su valor asociado a cada columna y sumando podemos determinar la cantidad asociada en base 10. Por ejemplo el número  579:

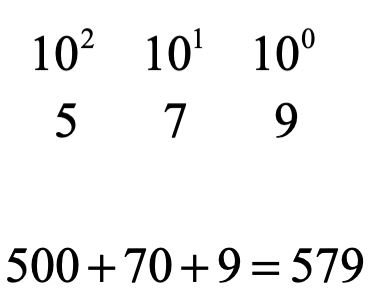
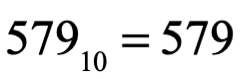
El valor de cada número de una cifra depende de su posición. 

Para un sistema posicional numérico de base 5, el conjunto de símbolos son 0,1,2,3,4,  ¿qué cantidad base 10 representa el número 2341 base 5?

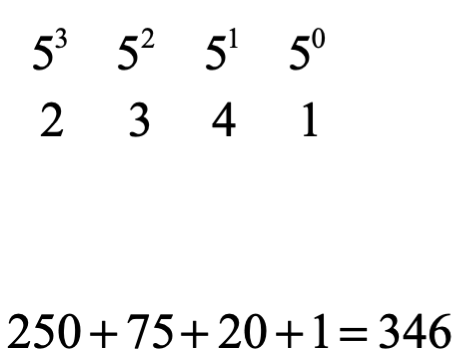
Resolviendo en Wolfram Alpha https://www.wolframalpha.com

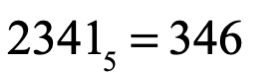
Para un sistema numérico posicional de base 16, el conjunto de símbolos es 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F, ¿qué cantidad base 10 representa el número E3FD base 16? Donde A=10, B=11, C=12, D=13, E=14, F=15 en cantidad.

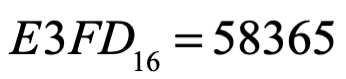
Podemos inventarnos cualquier sistema numérico posicional, por ejemplo uno de base 7, su conjunto de símbolos sería 0,1,2,3,4,5,6, ¿qué cantidad base 10 representa el número 4351 base 7?

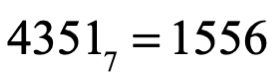
Podemos inventarnos un sistema numérico posicional de base 32, su conjunto de símbolos sería (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V), ¿que cantidad base 10 representa el sistema 89FMV base 32?

Para un sistema numérico posicional de base 2, el conjunto de símbolos es (0,1) ¿qué cantidad base 10 representa el número  10101101 base 2?

Con los sistemas numéricos podemos contar toda clase de objetos de la realidad. Pero, si no hubiera nada allí, no habría necesidad de contar, simplemente introducimos el número cero o incluso parece menos necesario utilizar números negativos, por ejemplo,  la expresión - 8 chivos para los hombres antiguos hubiera parecido sin sentido.

Para ver de un modo natural el concepto de cero y los números negativos en nuestra época, podemos imaginar 0ºC, -5ºC. Pero los conceptos de cero y números negativos llevaron miles de años para emerger, aunque en nuestro tiempo parecen muy naturales. Las primeras apariciones de los números cero y los negativos se presentaron probablemente en el comercio. Las ganancias fueron registradas como números positivos, las deudas con números negativos y cero el equilibrio. 

Hace algunos años se desarrollaba una amplia discusión en cuanto a si el nuevo milenio debe comenzar en el año 2000 (que lo hizo) o en el 2001 (desde el siglo XX comenzó en el 1901). El problema surgió porque no había ningún año 0. Los términos “antes de Cristo AC” y “después de Cristo DC”, fueron introducidos en el año 531 por Dionysus Exiguus, pero él no los podía establecer como año 0, porque para ese año no se había introducido año 1 AC inmediatamente después del año 1 DC. Un sistema más natural fue introducido en 1740 por el astrónomo Jacques Cassini, él elige seleccionar como año 0 justo el año de nacimiento de Cristo y manteniendo los años AC y DC justo uno antes y uno después de 1, por lo tanto el milenio sin duda inició en el año 2000.

Antes de continuar, debemos distinguir claramente entre cero y nada. Cero es un número como cualquier otro número, solo que este representa indeterminación de cantidad, si dividimos la unidad entre infinito, es decir 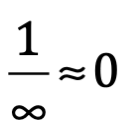, es la incertidumbre de aproximarnos a la nada. Mientras la nada significa la ausencia de cualquier cosa, incluyendo cantidad en sentido abstracto. 

Desde este punto, los números naturales son la base de un sistema numérico y la cuenta infinita dentro de este sistema son también números naturales, dado que son cuentas de unidad en unidad como proceso natural. La idea de número se aplica con los conceptos de cero y negativos, generando a la familia de números enteros. Los enteros son los números naturales positivos, los negativos y cero. Tenga en cuenta que 0 es identidad aditiva para nuestros sistemas de numeración, es decir, añadiendo cero a cualquier número no le produce cambio, si x es una variable que recibe números, entonces sí sumamos cero,  x+0=x, para todo x.  Así como 1 es el elemento neutro bajo la multiplicación:

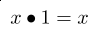
Ni Griegos, ni Egipcios utilizaron al cero, en su estilo geométrico de ver a la aritmética, el número a menudo es representado por longitudes de líneas, así que 0 o longitud cero habría sido difícil de imaginar. Pero los mesopotámicos con su sistema numérico de base 60, aún sin dejar huecos para indicar ninguna entrada de números en esa posición, en el cero se espera que el valor previsto en dicha posición sea un comodín para marcar el salto del final al principio de la base numérica, en tal caso lo empleamos hoy en día. Pero ese cero no tiene concepto para emplearse al modo de cálculo, el cero para el cálculo lo introducen los Mayas  . Es decir, en términos modernos, una aproximación a la nada de manera infinitesimal en base 10.

El cero Maya nos dice para la geometría, que un infinitesimal 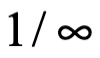dimensional en el espacio, tiene largo, ancho y alto. Es decir, el cero dentro de un sistema geométrico representa el origen del sistema y es un infinitesimal de tres dimensiones de algo que existe en ese espacio. 

Los Indios sin embargo, desarrollaron un sistema numérico decimal basado en los números 1 a 9 y más adelante introducen el cero, estos diez dígitos podían representar cualquier número entero, por grande que fuera. Pero el cero indio representó el conjunto vacío, es decir, la nada. Pero en su sistema el cero representó un comodín para la transición de la secuencia de la base numérica. 

Desde este momento en adelante el cero podría ser utilizado en la aritmética de números enteros negativos y positivos. Después de haber tratado con la suma, resta y multiplicación en donde el cero, el uno y los negativos mostraron coherencia total en la aritmética, pero con la atención de la división restrictiva de cualquier número entre cero, 

0/0=0

a/0=? No está definido, donde a es cualquier entero diferente de cero. 

Pudiéramos decir que a/0 es infinito, pero infinito no es un número y no obedece a las reglas de la aritmética, por ejemplo: 

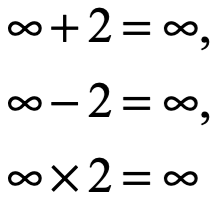
La división sobre cero de un número diferente de cero, no está definido, es una incoherencia dentro de las matemáticas, basta con emplear una computadora y programar en ella una división sobre cero, el código de computadora provocará que el sistema se vuelva inestable.

De los números naturales, pasamos a los números enteros, ahora pasaremos a los números reales que agregan otras dos clases de números. Otros tipos de números surgen de la división, estas fracciones pueden ser racionales o irracionales, en ellos están los números pi y e. Y al conjunto que agrupa a los números naturales, enteros, fraccionarios positivos y negativos se le llama, conjunto de números reales. Pero es hasta que cero es establecido en el cálculo cuando los fraccionarios se desarrollan. 

El uso del cero en cálculos aparece en las diferencias, 4 - 5=-1, y la diferencia de 5 -5=0 ajustando el estatus matemático a los negativos y la neutralidad de cero:

1+0=1;  5-0=5;  0+0=0;  0-0=0; 0-4=-4.

A partir de aquí, cero es parte del sistema aritmético. Reservando que no está definida la  división de los números entre cero.

Después de haber tratado con la suma, la multiplicación y la resta, se atendieron los números positivos o negativos a/b, donde b es distinto de cero. Mientras 0/0=0 es una definición vacua. 

El camino a los números reales se abre después de que tenemos claro que a/a es un número entero, que los hay positivos y negativos y cero. De los fraccionarios podemos deducir que en ellos habitan los números enteros positivos, negativos y el cero. Al romper un número en fracciones nos permite la división del número. Al multiplicar una fracción simplemente multiplicamos denominador por denominador y numerador por numerador de las fracciones:

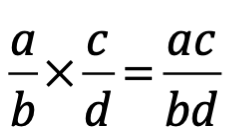
Para sumarlos o restarlos, primero colocamos a los fraccionarios con denominador común y luego procedemos a la resolución de una suma modesta. 

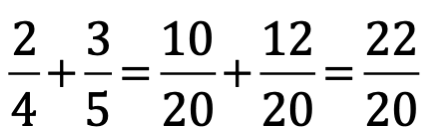
Las fracciones ya estaban plenamente establecidas para el momento en que el cero apareció en la escena, particularmente en los problemas de comercio entre sociedades. 

[1] Vinogradov, I. M. (2016). Elements of number theory. Courier Dover Publications.

[2] Einstein, A., & Engel, A. (1987). The collected papers of Albert Einstein (7). Princeton University Press.

[3] Pagano, S., Lombardi, L., & Mazza, V. (2014). Brain dynamics of attention and working memory engagement in subitizing. Brain Research, 1543, 244-252.

[4] Menary, R. (2015). Mathematical cognition: A case of enculturation. Retrieved from https://philarchive.org/archive/MENMCA-2

[5] Revkin, S. K., Piazza, M., Izard, V., Cohen, L., & Dehaene, S. (2008). Does subitizing reflect numerical estimation. Psychological science, 19(6), 607-614.

[6] Maloney, E. A., Risko, E. F., Ansari, D., & Fugelsang, J. (2010). Mathematics anxiety affects counting but not subitizing during visual enumeration. Cognition, 114(2), 293-297.

[7] Piazza, M., Fumarola, A., Chinello, A., & Melcher, D. (2011). Subitizing reflects visuo-spatial object individuation capacity. Cognition, 121(1), 147-153.

[8] Maloney, E. A., Risko, E. F., Ansari, D., & Fugelsang, J. (2010). Mathematics anxiety affects counting but not subitizing during visual enumeration. Cognition, 114(2), 293-297.

[9] Baddeley, A. (2001). The magic number and the episodic buffer. Behavioral and Brain Sciences, 24(1), 117-118.

[10] Shimomura, T., & Kumada, T. (2011). Spatial working memory load affects counting but not subitizing in enumeration. Attention, Perception, & Psychophysics, 73(6), 1694-1709.

[11] Braconier, H., & Ruiz-Valenzuela, J. (2014). Gross earning inequalities in OECD countries and major non-member economies.

[12] Anderson, J. R. (1982). Acquisition of cognitive skill. Psychological review, 89(4), 369.

[13] Domingos, A., & de Lisboa, N. APRENDIZAGEM DE CONCEITOS MATEMÁTICOS AVANÇADOS: O CONCEITO DE DERIVADA.

[14] Gaber, D., & Schlimm, D. (2015). Basic mathematical cognition. Wiley Interdisciplinary Reviews: Cognitive Science, 6(4), 355-369.

[15] Núñez, R. E., & Sweetser, E. (2006). With the future behind them: Convergent evidence from Aymara language and gesture in the crosslinguistic comparison of spatial construals of time. Cognitive science, 30(3), 401-450. doi:10.1207/s15516709cog0000_62

[16] Boroditsky, L., & Gaby, A. (2010). Remembrances of times East: absolute spatial representations of time in an Australian aboriginal community. Psychological Science, 21(11), 1635-1639.

[17] Bluedorn, A. C., & Standifer, R. L. (2006). Time and the temporal imagination. Academy of Management Learning & Education, 5(2), 196-206.

[18] Meredith, M. (2011). The fate of Africa: A history of the continent since independence. Hachette UK.

[19] Carl Zimmer (2018) Neanderthals, the World’s First Misunderstood. The New York Times.

[20] Herrmann, E., Hare, B., Call, J., & Tomasello, M. (2010). Differences in the cognitive skills of bonobos and chimpanzees. PloS one, 5(8), e12438.