Primer semestre: Pensamiento aritmético

Unidad Cuatro: Comprender los conceptos de potenciación y radicalización para realizar operaciones con exponentes y radicales. 

4.1 Los números reales

Estos números reales son el cuerpo o campo cerrado bajo una operación binaria (+,x), llamando a esta álgebra aritmética, cuyas propiedades son:

Definiciones:

Los números naturales 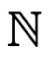son los que van del 1 hacia el infinito: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11… es decir, son números positivos que sirven como índice para contar los elementos de un conjunto.

Un número entero 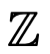es cualquier elemento del conjunto formado por los números naturales, sus opuestos (versiones negativas de los naturales) y el cero. Estos son: Los naturales (o enteros positivos): +1, +2, +3, +4, +5... El cero, que no es ni positivo ni negativo.

Los números racionales 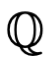 hacen referencia a aquellos a/b que permiten conocer el cociente entre dos números enteros. También llamados fraccionarios.

El conjunto de los números irracionales 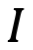se representa por a/b y está formado por todos los números decimales cuya parte decimal tiene infinitas cifras periódicas, es decir, por todos los números que no se pueden representarse por el cociente de dos números enteros.

4.2 Potencias

Un número es un conjunto que expresa la cantidad de sus elementos. Esperamos que A siendo un número, sea un conjunto finito. Dado un conjunto A, a la colección de todos los subconjuntos de A se denominan conjuntos de potencia de A. Si lo escribimos así P(A); o otra notación más común es por ejemplo para el número dos: .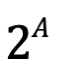

Si 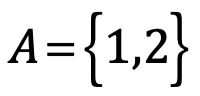, entonces P(A)={0,1,2,3}

El conjunto de potencias parte del conjunto vacío, un conjunto cuyo elemento único es el vació. 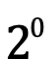=1 Todo conjunto de potencias contiene a la potencia cero, donde solo tiene un elemento. Todo número a la cero por tanto, es igual a uno.

Si A=1 la Potencia P(A)= 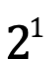=2

Si A=2 la Potencia P(A)= 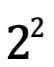=4

Si A=3 la Potencia P(A)= 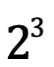=8

A es un conjunto finito de n elementos. P(A) es un conjunto finito de 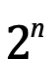elementos. Si n=0 entonces P(A)=1. Esto es verdadero por inducción para todos los números elevados a la potencia cero. 

Potencia de un número a, es el producto de este tantas veces n.

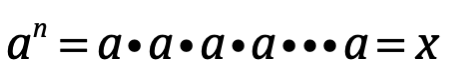, n veces.

Donde x, es producto del factor a, n veces.

El signo de 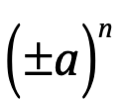es positivo si es par y negativo si es impar. 

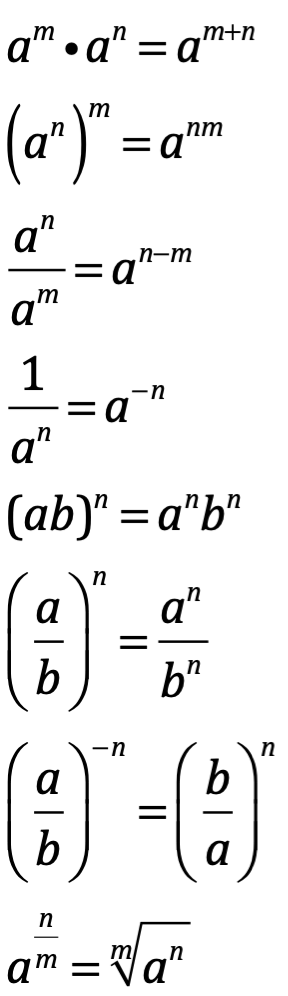
Si P(A) + P(A) =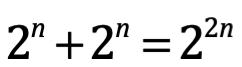

Si P(P(A))=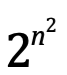

Si P(A) donde no tienen porque ser solo positivos a y n.  

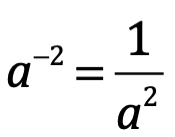
Pero a y n no necesariamente deben ser solo número enteros positivos, podrían ser cualquier número real o complejo. 

Un tema relacionado con las potencias es el de factorial de un número.

Sea 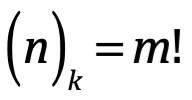el número de formas de muestrear k veces desde un conjunto n de elementos. Donde el resultado m factorial es definido como:

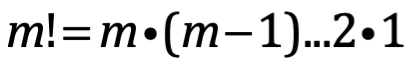
3!=3x2x1=6

12!=12x11x10x9x8x7x6x5x4x3x2x1=479001600

Cuando se desea trabajar con números elevados a una potencia de base 10, esta notación exponencial generalmente nos conduce a la notación científica de los números.

4.3 Radicación

La raíz 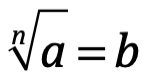(es un signo de radical), si y solo si bⁿ=a. Donde a es la cantidad radicando, exigiendo esta ser positiva en los reales, caso contrario será una cantidad imaginaria y, n es el índice del radical o grado del radical. Es una operación inversa del exponencial. Si la expresión es racional la raíz es exacta y si no es irracional. Un radical tiene tantas raíces como el grado del radical. El valor aritmético del radical puede ser resuelto para un 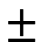. Por ejemplo 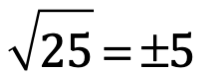. Además de las leyes de los exponentes agregaremos las de los radicales:

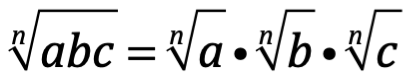
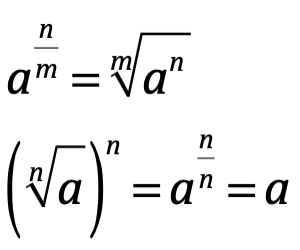
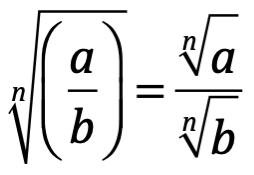
4.4 Notación científica

La notación científica es una forma de expresar números como el producto de dos números: un coeficiente y el número 10 elevado a una potencia. Es una herramienta muy útil para trabajar con números que son muy grandes o muy pequeños. Como ejemplo, 160,000,000,000 metros, una distancia muy grande. En notación científica, la distancia se escribe como 1.6 × 10¹¹ m. El coeficiente es 1.6 y debe ser un número mayor o igual que 1 y menor que 10. La potencia de 10, exponente 11, tendría que multiplicar 1.6 por 10¹¹ para obtener el número correcto. La notación científica se refiere a veces como notación exponencial. Un resumen de las unidades del Sistema Internacional de Unidades SI se da en la tabla a continuación. Observe que cuando son números pequeños el exponencial es negativo. 

Para escribir un número grande en notación científica, primero debemos mover el punto decimal al primer número de la cifra entre1 y 10. Como mover el punto decimal cambia el valor, tenemos que aplicar una multiplicación por la potencia de 10 que nos resulte en un valor equivalente al original. Para encontrar el exponente, solo contamos el número de lugares que recorrimos el punto decimal. Ese número es el exponente de la potencia de 10. De la forma ax10ⁿ donde a 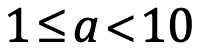o 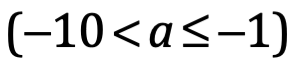y n es un entero.

Por ejemplo:

54,000,000.00 a notación científica: 5.4x10⁷ 

0.0007 a notación científica: 7x10^-4

El teorema fundamental del Aritmética dice: cada número natural o es primo o puede ser escrito como un producto de primos. Este teorema no lo abordaremos dado que esta fuera de nuestro alcance curricular, pero nos permite darnos cuenta que hay una factorización única para cada número natural y que la aritmética es un campo fascinante que no termina en este enfoque tan básico expuesto aquí. 

4.5 El plano complejo

Los números reales incluyen a los racionales e irracionales, que corresponden a todos los puntos de una línea infinita llamada línea real. Parece indiscutible que el cuadrado de un número negativo es positivo, puesto que el cuadrado de un número real es no negativo, cumpliendo la ecuación:

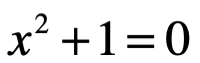
Es Raphael Bombelli en 1526 quien introduce el número complejo, fue en su obra L’Algebra^[1], donde se observa a simple vista que la ecuación anterior no tiene ninguna solución real (raíces). Sin embargo, Roger Penrose destaca que, al superarse concebirlo imposible, por un enfoque razonable que exige otro sistema de números que sea adecuado para tales propósitos, en que nos permita resolver la ecuación^⁠[2]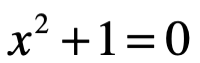. Para este caso la ecuación algebraica general de grado n, donde  son números reales cualesquiera.

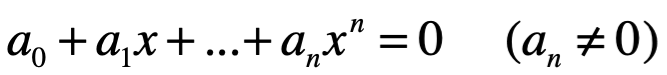
Este objetivo solo puede lograrse si conseguimos extender el sistema de números reales por otro que es parte, lo hacemos con un sistema de numeración de otro más extendido. 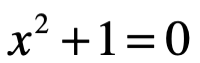es en cierto sentido la ecuación algebraica más simple sin raíces reales, un primer acercamiento evidente para nuestro problema es introducir una unidad imaginaria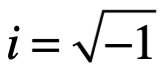, es decir, una nueva dimensión y entonces el plano numérico se extiende al número complejo de la forma:

,

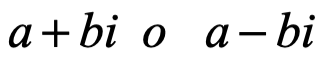Donde a y b son números reales arbitrarios y la operación de estos números se define de manera natural como binomios 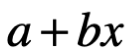donde x es desconocida, salvo en este caso: 

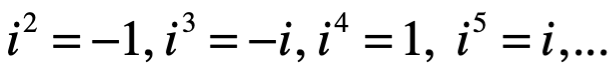
Sí b=0, observamos que solo está presente la línea real con sus características especiales. Asombrosamente como veremos resulta que una vez que permitimos que x tome valores complejos, la ecuación general algebraica siempre tiene una raíz, aunque los coeficientes 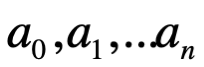 sean números complejos, un resultado que es conocido como el teorema fundamental del álgebra: establece que todo polinomio de grado mayor que cero tiene una raíz. 

Por número complejo nos referimos a una expresión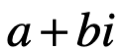, donde a y b son números reales e “i” es la unidad o dimensión imaginaria. Si a es la parte real de c, escrita como Re c, b es llamada la parte imaginaria de c, escrita como Im c. El número complejo cero es 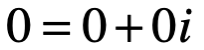, donde las partes imaginaria y real valen cero. Por definición dos números 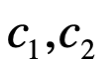son iguales solo sí 

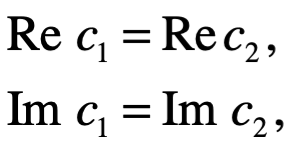
Si Im c=0, c=a+bi se reduce a un número real, mientras que 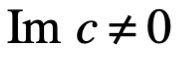, se dice que c es puramente imaginario. Los números complejos pueden ser representados geométricamente como puntos en el plano, un hecho que no solo es útil, sino prácticamente indispensable para la ingeniería y la aplicación científica moderna de este “mágico número”, como lo llama Roger Penrose. Con la introducción de un sistema de coordenadas rectangulares en el plano, podemos identificar el número complejo , como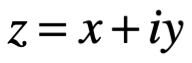, asociado con el punto P.

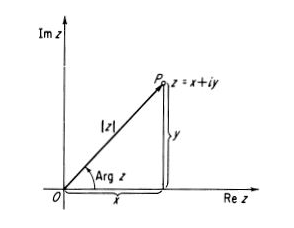
De esta manera, establecemos una correspondencia biunívoca entre el conjunto de todos los números complejos y el conjunto de todos los puntos en el plano con una precisión infinita dado que las partes Re y Im son números racionales e irracionales. Claramente, con esta asignación, el conjunto de todos los números reales en el eje x y el conjunto de los números puramente imaginarios en el eje y, mientras que el conjunto de los números 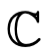corresponden al plano complejo o llamado plano z, en el entendido que tal plano z es construido por términos 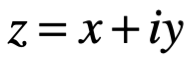que son los puntos que definen la densidad de la superficie z. Otra manera de representar al número complejo es usar el vector posición que une el origen con algún punto en el plano z^[3]. El vector 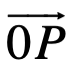cuyo módulo o norma está dado por el valor absoluto del número complejo z, denotado por . El ángulo de dirección entre el eje real y el vector 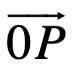, es positivo solo si la rotación es en el sentido antihorario y negativo en el sentido contrario; se llama argumento del número complejo z y se denota por Arg z. En otras palabras  y 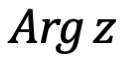son las coordenadas polares.

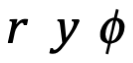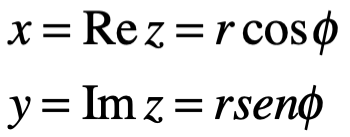
Por lo tanto:

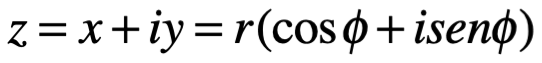
Esta última forma es la que se llama forma trigonométrica de un número complejo z. Claramente Arg z, se define solo en un múltiplo entero de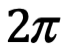 . Sin embargo, existe uno y solo un valor de Arg z, es decir de 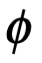, que satisface la desigualdad:

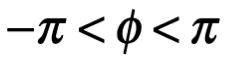
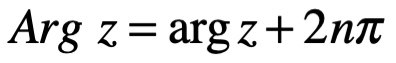
donde n se extiende sobre los números enteros positivos y negativos incluyendo al cero. 

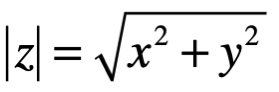
y

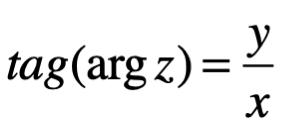
Se requiere algún cuidado en invertir la expresión de la tangente, puesto que el arco tangente de un número real x, es escrito como Arc tan x, y se define solo para múltiplos enteros de . Sin embargo, existe uno y solo un valor de Arc tan x, digamos un 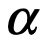que satisface la igualdad: 

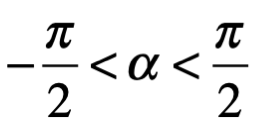
y llamaremos al valor 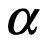, el valor principal del arco tangente de x, escrito arc tan x.  Nosotros ahora podemos invertir la relación 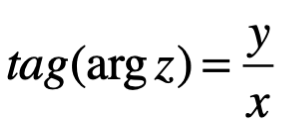, obteniéndose:

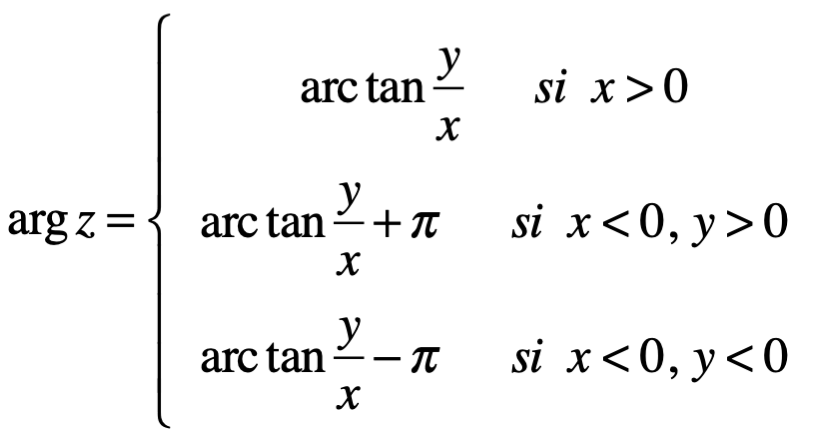
Por otra parte, 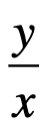se convierte en infinito, claramente si tenemos: 

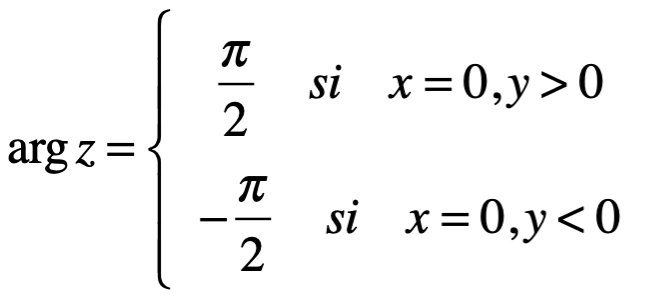
mientras que el caso z=0 es indeterminado como la versión Maya del cero.

Los números complejos:

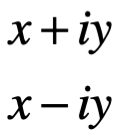
se dice son números complejos conjugados, si uno de estos se denota por z, y el otro se denota por o .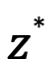

Obviamente los puntos z y son simétricos con respecto al eje real x.  

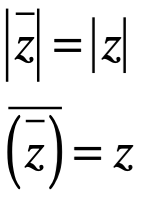
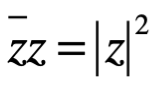
Por otra parte

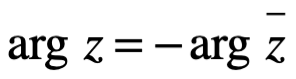
A menos que z sea un número con la parte real negativa, en cuyo caso:

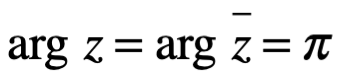
La ecuación de Euler o llamada por otros, identidad de Euler: 

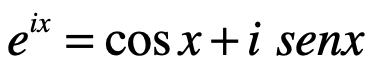
donde i es la unidad imaginaria. Tenga en cuenta que la identidad de Euler es poliédrica y a veces también se llama la fórmula sobre una curvatura Euler. La expresión equivalente:

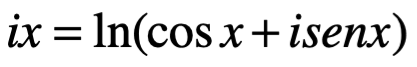
previamente había sido publicada por Costas (1714). El caso especial de la fórmula con 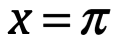  da la identidad:

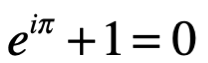
Una ecuación que conecta los números fundamentales, e, 1 y 0 (cero), las operaciones fundamentales +, ×, y exponenciales, la relación más importante =, y nada más. Gauss comento que esta fórmula no era inmediatamente obvia.

La fórmula de Euler se puede demostrar utilizando un desarrollo de series:

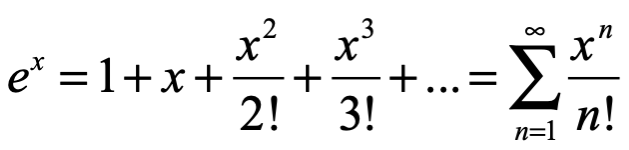
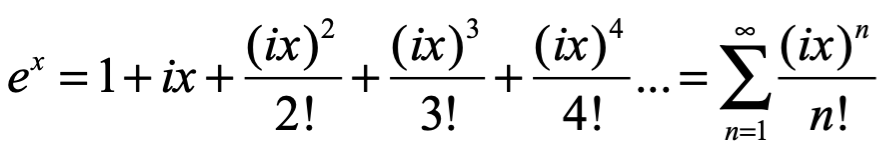
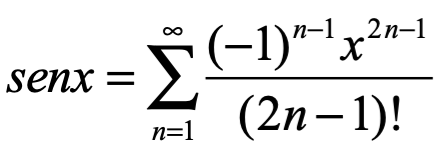
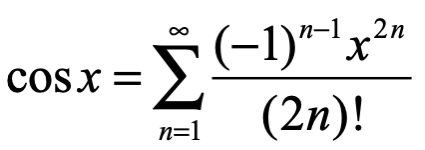
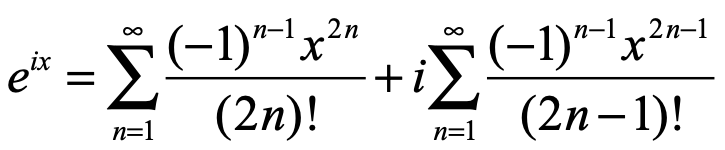
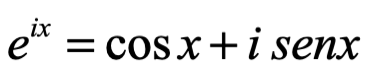
Aplicando a ambos miembros de la igualdad la exponencial: 

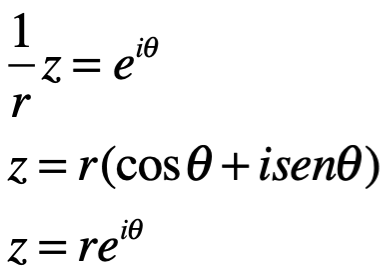
Donde r representa la magnitud de z y es el argumento de z, usualmente llamado arg z.

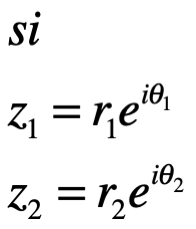
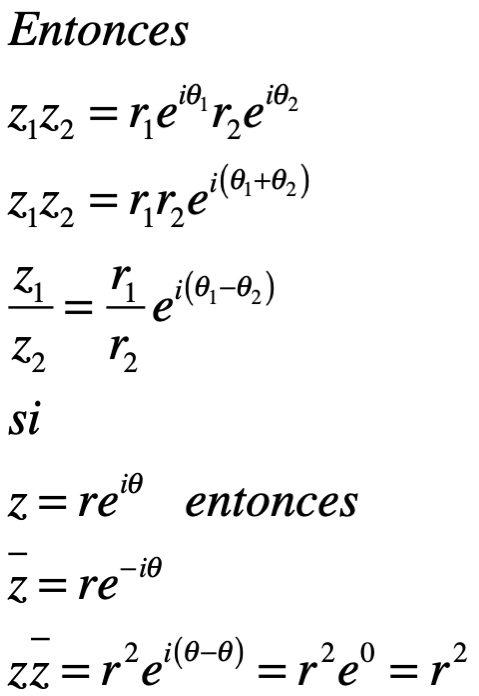
Potencias de complejos 

Ejemplo 1. Determine el valor de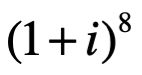

Sabemos que: 

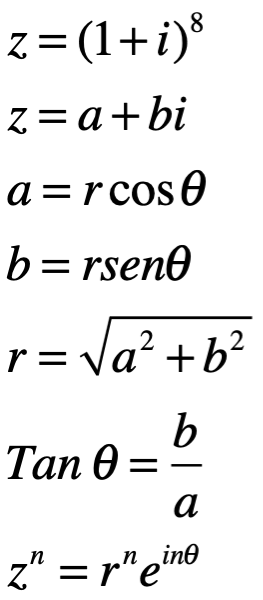
Solución:

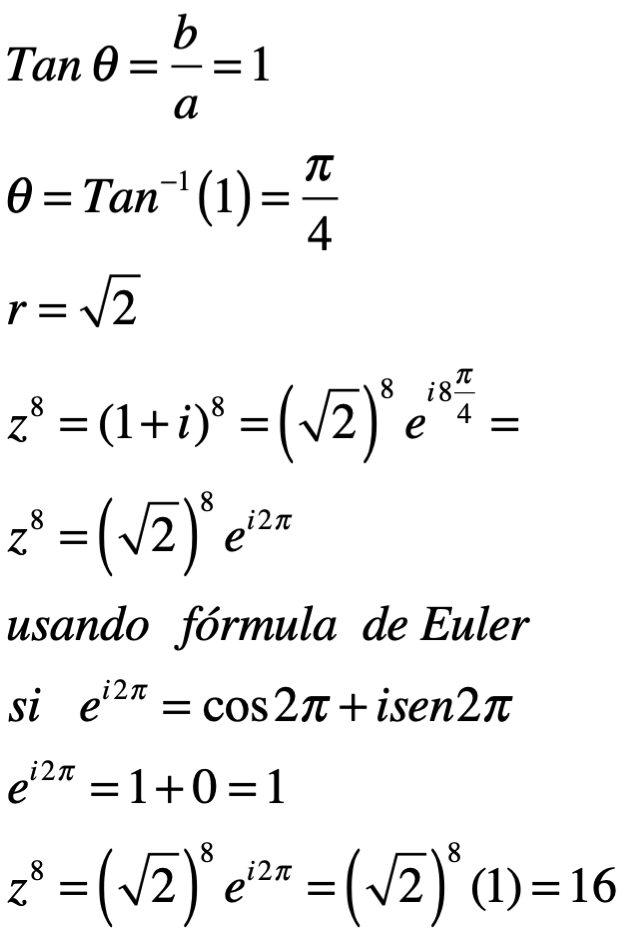
Ejemplo 2. Determine el valor de

Solución: 

Ejercicio 1. Determine el valor de escribiendo el procedimiento.

Solución: 

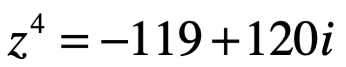
La ecuación 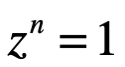donde n es el valor complejo de raíces n-esima de la unidad, es decir, se dice “cada raíz tiene una magnitud de”.  Ahora que:

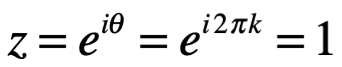
Usando la ecuación de Euler:

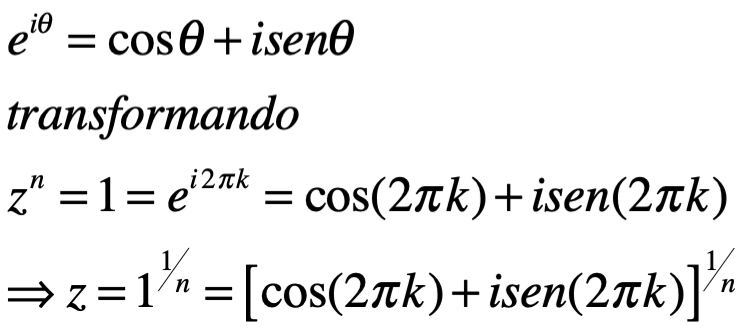
Ahora nosotros usamos la fórmula e  De Moivre que establece:

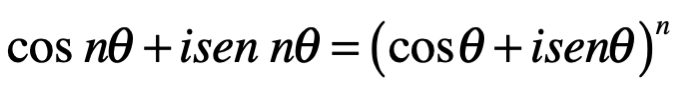
Así que:

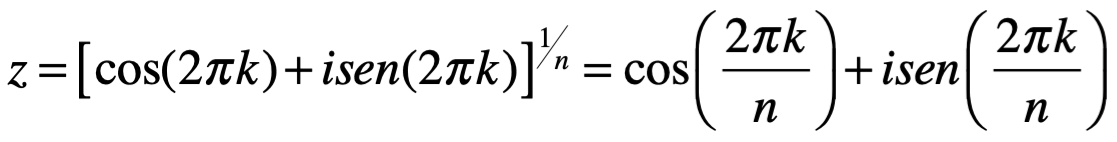
Donde k es cualquier número entero. Ahora está claro que todas las n raíces de z deben estar en un círculo de radio 1, y las expresiones del tipo 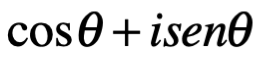son típicamente de la forma:

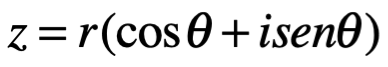
Pero en este caso r=1, por lo tanto:

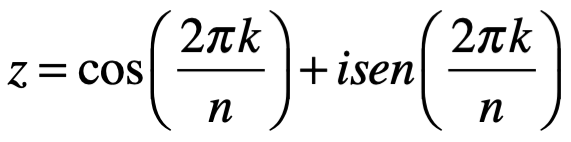
4.6 Álgebra compleja 

Se deduce de su tratamiento como binomiales, suma y producto de dos complejos: 

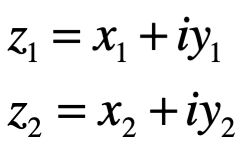
están dados por:

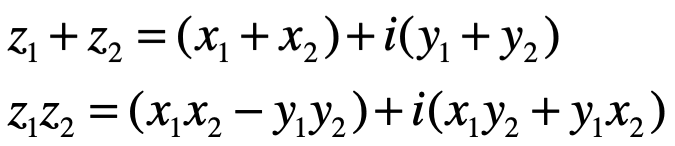
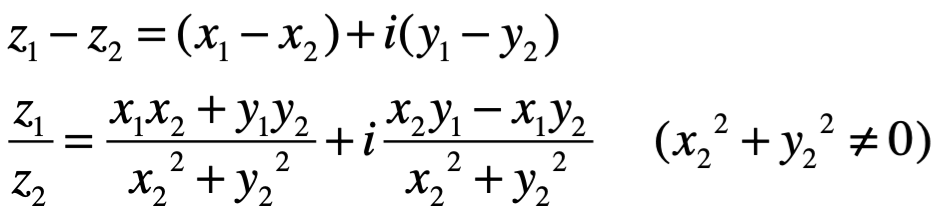
Álgebra compleja es un campo para el que se cumplen las propiedades axiomáticas de toda álgebra, dados los números complejos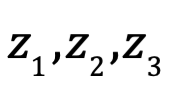  

Conmutativa bajo +

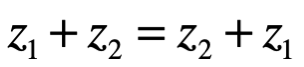
Conmutativa bajo

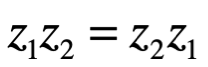
Asociativa bajo +

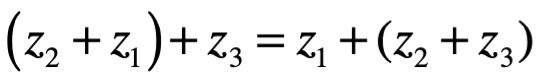
Asociativa bajo

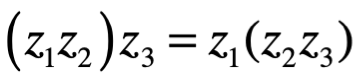
Distributiva  bajo la +

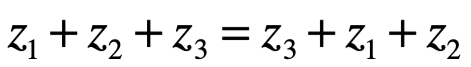
Distributiva  bajo la

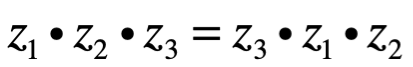
Elemento neutro bajo la +

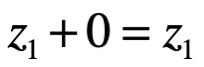
Elemento neutro bajo la

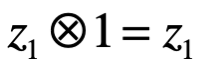
Inverso simétrico

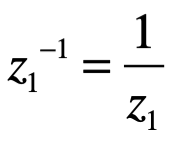
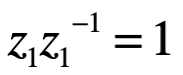
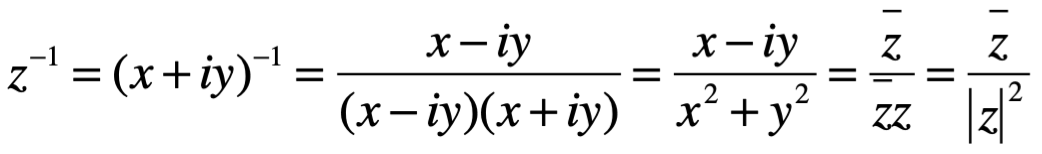
Hasta lo visto aquí, uno podría representar a los números complejos como pares ordenados (sin emplear la unidad imaginaria i).

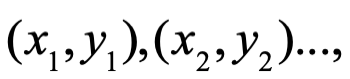
donde 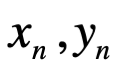 son números reales, entonces multiplicación y adición pueden ser representadas:

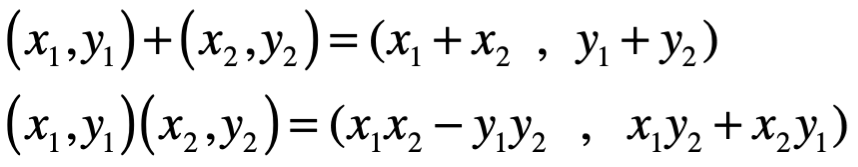
Con este enfoque, la relación 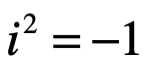tiene como análogo: 

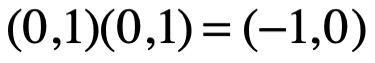
Hemos visto que la explicación de la extensión de los números reales a los números complejos no es menos exquisita que la extensión de los números enteros a los racionales y su posterior extensión de los racionales a los irracionales implicados en el concepto de una línea continua.

Ejercicios aritmética de complejos

Ejercicios 1: Represente los siguientes números complejos en su forma trigonométrica:

1. 1+i
2. -1-i
3. 1-i
4. 

[1] Teresa Lucca, Ana M. (2013). Blog de matemáticas y TIC’S.

[2] Penrose Roger (2007). El camino a la realidad. Barcelona: DEBATE.

[3] Conway, J. H. & Guy, R. K. (1996). Euler's Wonderful Relation. The Book of Numbers. New York: Springer-Verlag.