Primer semestre: Pensamiento aritmético

Unidad Cinco: Comprender los conceptos de medición a partir del análisis de los procesos sociales que llevaron a su desarrollo para aplicarlo en situaciones de interés. 

5.1 Concepto de medición

Mensurar es tratar matemáticamente la realidad como variables que expresan la cosa observada o sometida a medición. Las variables se describen como parámetros cuando es posible observarlas “directamente”, y como indicadores cuando la observación es indirecta. En la física, una vez definida una cosa por su mensuración, la cosa se desmaterializa en cantidades escalares o vectoriales. Los mensurandos son categorías de la existencia física.

Mensurar es medir mediante patrones de referencia y determinar la confianza en los datos. Cuando medimos —es decir, cuando determinamos alguna cantidad particular (o mensurando)— lo que obtenemos es información más incertidumbre. La medición consiste en determinar los mensurandos de una cosa, definiéndolos en términos de hechos físicos, del método de observación y del proceso de medición.

Es importante definir qué es un principio de medición físico por su relevancia para generar conocimiento de la realidad física. Estos principios justifican los fundamentos teóricos y técnicos que respaldan la objetividad científica de la observación. Además, debemos considerar criterios de valor sobre los datos generados en términos de precisión —dada por la repetitividad y la reproducibilidad del acto de medir—; estos criterios son necesarios para garantizar la calidad de los datos. La medición implica definir el objetivo (mensurando), el procedimiento, los instrumentos, el entorno, el observador y el método de cálculo.

El método justifica la secuencia lógica de operaciones que instrumenta un principio de medición físico. Los instrumentos son soportes tecnológicos que extienden nuestros sentidos para observar la realidad, pero también pueden engañarnos por errores de calibración, errores metodológicos o por el ruido del entorno. El ruido del entorno es un conjunto de señales impredecibles que interfieren con las lecturas de los instrumentos de medición. Los instrumentos tienen rangos de operación en los que pueden indicar cambios en las variables medidas; por ejemplo, la deriva instrumental es el cambio más pequeño al que es sensible el instrumento de medición. El entorno se define por aquellas variables no controladas o semicontroladas que alteran los datos generados por los instrumentos.

Un dato de medición posee, de acuerdo con Heisenberg, un factor de incertidumbre generado por el entorno, por errores de apreciación del operador y por los efectos del propio instrumento al interactuar con el sistema a medir. Ningún dato instrumental es, en lo absoluto, solo información: no es un reflejo exacto que coincida con el mensurando. El error es la diferencia entre el dato instrumental y el valor real del mensurando. La incertidumbre de una medición es un factor asociado al dato —la dispersión del valor que razonablemente puede atribuirse al mensurando. 

Por ejemplo, la incertidumbre estándar tipo A se evalúa mediante el análisis estadístico de una serie de observaciones. Si x1,x2,…,xN son N observaciones y 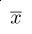su media, la desviación muestral viene dada por

Si el resultado de la medición se expresa como la media de las observaciones, la incertidumbre estándar tipo A asociada a la media es

Aquí  u(media) denota la función de incertidumbre asociada a la medición  M.

Donde la desviación estándar experimental de la media, cuantifica que también 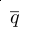estima el valor esperado de q, y se puede utilizar  como una medida de la incertidumbre estándar de un conjunto de mediciones 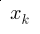, tal como se definió en líneas atrás.  Por ejemplo, cuando en ciencia se da la cifra de  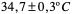, se refiere a la incertidumbre, indicando que el mensurando se encuentra entre  35º y 34.4º C.

Antes de profundizar en un modelo de medición bajo el paradigma ISO (Organización Internacional de Normalización, o en inglés International Organization for Standardization), debemos anticipar que la competencia de medición moderna contempla el cálculo de la incertidumbre y de la trazabilidad como conceptos metrológicos fundamentales.

Para la norma ISO 3534-1 (ISO, 1993), incertidumbre es “una estimación unida al resultado de un ensayo que caracteriza el intervalo de valores dentro de los cuales se afirma que está el valor verdadero”, o en otros términos, “un parámetro asociado al resultado de una medida, que caracteriza el intervalo de valores que pueden ser razonablemente atribuidos al mensurando”. Recordemos que el mensurando es un atributo sujeto a medida. La incertidumbre se relaciona con la calidad del resultado de medición, con el costo tecnológico de producir el dato y con la complejidad del manejo operativo de las mediciones.

La trazabilidad es un método gráfico de control que ayuda a demostrar la fiabilidad de los resultados. Estos conceptos permiten comparar la calidad de las mediciones ofrecidas por diferentes laboratorios.

Por exactitud entendemos la diferencia entre el resultado y el valor de referencia. Este término revela la existencia de un sesgo sistemático en las mediciones. Podemos inferir que la exactitud resulta de la combinación de los efectos de precisión y veracidad; en otros términos, exactitud es la variabilidad de los resultados más la veracidad obtenida por métodos de referencia certificados.

Para la ISO 3354, precisión es “el grado de concordancia entre ensayos independientes obtenidos bajo unas condiciones estipuladas”.

Toda medición sobre una magnitud física (mensurando) implica siempre disponer de una unidad de referencia (valor unitario), a fin de producir datos que crearán una imagen de la realidad en forma de información empírica. Tengamos en cuenta que la información empírica es la que surge de la experiencia de medición, y esta nunca será absoluta en términos de ausencia de incertidumbre.

Las unidades de medida de referencia se organizan históricamente en el Sistema Internacional de Unidades (SI), bajo la autoridad de la Oficina Internacional de Pesas y Medidas (CGPM), con sede en París, de la cual México es miembro. Al pertenecer, se autoimpone las convenciones de patrones de referencia, escalas de medidas físicas, comparaciones entre patrones internacionales y técnicas de medida, comprometiéndose a adoptar estos criterios para aplicarlos al desarrollo, la economía, el comercio, la ciencia, la técnica y al lenguaje educado de sus ciudadanos.   

5.2 Unidades de medida y sistema internacional

De acuerdo con el SI, una magnitud es el coeficiente que multiplica a una unidad de referencia, y la unidad es una convención internacional tomada como referencia dentro del sistema. Las magnitudes son cantidades escalares: pueden expresarse de formas diferentes sin que cambie lo que representan. Por ejemplo, la velocidad puede expresarse en metros por segundo o en kilómetros por hora, sin que ello refiera a una magnitud distinta.

Antes de disponer de un sistema de unidades, requerimos de un sistema de magnitudes en referencia a unidades básicas, y de estas derivar todas las demás, que se llamarán unidades derivadas. Habrá entonces magnitudes básicas y magnitudes derivadas. Desde la física, esta división no es esencial para el conocimiento en sí, pero sí para la organización práctica de las mediciones. Conviene tener presente que las unidades derivadas corresponden a ecuaciones algebraicas que relacionan magnitudes básicas.

Si bien las unidades básicas son finitas, las derivadas pueden expresarse sin límite. Conforme la ciencia y la ingeniería avanzan, se crean nuevas magnitudes derivadas a partir de otras ya conocidas. La medición es siempre una convención compartida que hace posible traducir la experiencia en conocimiento comunicable. La distinción entre unidades básicas y derivadas no es tanto una verdad de la naturaleza, sino una herramienta para ordenar el pensamiento y garantizar que la práctica científica pueda crecer de manera acumulativa.

Tabla 1. Unidades básicas del SI 

Tabla 2. Definiciones de las unidades básicas del SI 

Tabla 3. Ejemplos de unidades derivadas expresadas en términos de las unidades básicas del SI 

Tabla 4. Unidades derivadas del SI con nombre y símbolos especiales 

Tabla 5. Prefijos del SI 

Tabla 6. Unidades fuera del SI aceptadas en cuanto a su uso 

Las dimensiones de las magnitudes físicas son formadas por las siete magnitudes básicas del SI.

Tabla 7. Magnitudes básicas y dimensiones en el SI

Otros sistemas muy utilizados son los sistemas Cegesimal de unidades (CGS) e Inglés, para los cuales requerimos unidades de conversión al SI.  

EQUIVALENCIAS DE LAS UNIDADES INGLESAS

LONGITUD:

1 milla = 1,609 m

1 yarda = 0.915 m

1 pie = 0.305 m

1 pulgada = 0.0254 m

MASA:

1 libra = 0.454 kg

1 onza = 0.0283 kg

1 ton inglesa = 907 kg

Unidades del sistema cegesimal o sistema CGS

5.3 Razón y proporción

Dentro del ámbito matemático, los conceptos de razón y proporción representan un núcleo fundamental para la comprensión de las relaciones cuantitativas. Su estudio no solo responde a una necesidad de cálculo, sino también a una exigencia epistemológica: establecer comparaciones entre magnitudes y garantizar, a partir de ellas, la posibilidad de medir, predecir y representar el mundo. Como advierte Lamon (2007), la transición del pensamiento aritmético al algebraico se sostiene precisamente en la capacidad de concebir relaciones proporcionales, lo cual confiere a estos conceptos un papel estratégico en la educación matemática y en el desarrollo de la ciencia.

Una razón puede definirse como la comparación entre dos cantidades homogéneas expresada mediante una división. Así, la razón entre a y b se denota como a:b o a/b, lo que significa cuántas veces una magnitud contiene a otra (Stewart, 2012^[1]). En este sentido, la razón constituye un acto intelectual que reduce la pluralidad a una relación ordenada, posibilitando la comparación y la jerarquización.

La proporción, en cambio, expresa la igualdad entre dos razones. La afirmación a:b=c:d implica que la relación existente entre las magnitudes a y b es idéntica a la que se establece entre c y d. Desde la perspectiva histórica, Euclides en Los Elementos sistematizó este concepto al convertirlo en piedra angular de la geometría, permitiendo establecer semejanzas entre figuras y resolver problemas de medición (Euclides, trad. Heath, 1956^[2]). En efecto, la proporcionalidad es un principio estructurante que conecta la aritmética, la geometría y, en tiempos modernos, el álgebra.

La aplicabilidad de razones y proporciones excede los límites de la matemática pura. En física, se utilizan para definir magnitudes derivadas como la velocidad —razón entre distancia y tiempo—; en economía, para analizar indicadores de cambio, elasticidad o tasas de interés; y en el arte, para producir armonías visuales, como lo demuestra la célebre proporción áurea (Livio, 2002^[3]). De este modo, la proporcionalidad actúa como un principio unificador entre campos diversos del conocimiento, reafirmando la universalidad del lenguaje matemático.

El estudio de razones y proporciones revela no solo un conjunto de herramientas de cálculo, sino una forma de organizar la experiencia y de proyectar conocimiento. Al establecer equivalencias entre relaciones, la mente humana se emancipa del dato aislado y accede a una visión estructural de la realidad. De ahí que estos conceptos, presentes desde la antigüedad griega hasta los métodos científicos contemporáneos, constituyan un pilar de la racionalidad matemática. Como advierte Lamon (2007^[4]), comprender la proporcionalidad es comprender la lógica misma de las relaciones, sin la cual la ciencia, el arte y la técnica perderían coherencia.

[1] Stewart, J. (2012). Precalculus: Mathematics for Calculus (6th ed.). Brooks Cole.

[2] Euclides. (1956). The Thirteen Books of the Elements (T. L. Heath, Trans.). Dover Publications.

[3] Livio, M. (2002). The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. Broadway Books.

[4] Lamon, S. J. (2007). Rational numbers and proportional reasoning. En F. K. Lester Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 629–667). Information Age Publishing.